Подклассы остовных подграфов

•Остовный k-регулярный (степень всех вершин равна k) подграф для произвольного натурального k ≥1 называется k-фактором графа G.

•Остовный 1-регулярный подграф носит название 1-фактор графа G, а набор ребер в таком подграфе называется совершенным паросочетанием в исходном графе G.

•Паросочетанием в произвольном графе G называется любой набор ребер, не имеющих общих концевых вершин.

•Паросочетание М называется совершенным, если оно покрывает все вершины графа

•Ребро e ∈ E в связном графе G называется мостом, если получающийся после его удаления граф G − e становится несвязным. В случае несвязного графа G мостом называется ребро, после удаления которого количество компонент связности увеличивается на единицу.

•Вершина x называется точкой сочленения графа G, если после ее удаления количество компонент связности графа G−x увеличивается по сравнению с количеством компонент связности исходного графа G.

•Утверждение. Вершина x в связном графе G, построенном на n > 3 вершинах, есть точка сочленения графа G тогда и только тогда, когда в G существуют отличные от x вершины y и z, такие, что x содержится в каждом пути из y в z.

•Утверждение. Ребро e = {x,y} в простом связном графе G является мостом тогда и только тогда, когда e не принадлежит ни одному из циклов графа G.

Поиск кратчайших путей во взвешенном графе. Основные понятия. Постановка задачи. Алгоритм Дейкстры, алгоритм Флойда, алгоритм Форда-Беллмана. Примеры.

Алгоритм Дейкстры:

• Дан ориентированный взвешенный граф G, причём вес любой дуги неотрицательный. Требуется найти кратчайшие пути от выделенной вершины s до всех вершин графа.

• Идея: объявить массив d, заполненный значениями 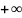всюду, кроме позиции s: d[s] := 0; организовать массив p предков вершин; массив used, где used[v] означает, что вершина v помечена. Изначально used заполнен значениями false.

• Организуем последовательность из n-1 итераций, на каждой из которых найдём непомеченную вершину v с минимальным d[v]. Пометим вершину v и переберём все дуги с началом в вершине v и проведём релаксацию вдоль этих дуг.

Алгоритм Форда-Беллмана.

• Дан ориентированный взвешенный граф G. Требуется найти кратчайшие пути от выделенной вершины s до всех вершин графа.

• Идея: объявить массив d, заполненный значениями всюду, кроме позиции s: d[s] := 0; организовать массив p предков вершин.

• Провести n-1 итераций с номерами от 1 до n – 1; на каждой итерации перебираем все дуги, пытаясь провести релаксацию вдоль каждой дуги.

Алгоритм Флойда-Уоршелла.

• Дан ориентированный взвешенный граф G. Требуется для всех пар вершин (u, v) найти кратчайшие пути от u до v.

• Идея: представим граф в виде матрицы смежности d, где:

1) d[v][v] = 0;

2) d[x][y] = W(x->y) если существует ребро из x в y, d[x][y] = +∞ иначе.

Совершим n итераций (с номерами от 0 до n-1), каждая из которых будет соответствовать некоторой вершине k. При выполнении итерации будем перебирать концы путей i и j и пробовать составить путь от i до j, на котором k будет промежуточной вершиной, т. е. будем проводить релаксацию, сравнивая d[i][j] и d[i][k] + d[k][j].

Восстановление пути от s до t:

9. Обходы графов: в ширину и глубину (рекурсивная и нерекурсивная реализация). Алгоритмы, основанные на алгоритмах обхода: нахождение компонент связности, поиск кратчайших путей, топологическая сортировка, проверка на ацикличность, проверка на двудольность, построение стягивающего дерева. Примеры.

BFS – поиск в ширину находит путь кратчайшей длины в невзвешенном графе; одинаково работает на ориентированных и неориентированных графах; работает за O(N+M).

DFS – поиск в глубину находит лексикографически первый путь в графе; работает за O(N+M).

Нахождение компонент связности можно проверить с помощью любого обхода: запуская алгоритм от каждой вершины и смотря на массив used можно узнать к какой компоненте связности принадлежит граф: вершины, принадлежащие этой компоненте, будут посещены, то есть used[v]=true. Для вершин в других компонентах связности used[v]=false.

Узнать кратчайшие пути от вершины s до каждой другой можно с помощью обхода в ширину и массива предков – p[v]=u означает, что в v попали через u. Таким образом, находим вершины в обратном порядке от конечной вершины до вершины s.

Проверка на двудольность: нужен дополнительный массив part, в котором каждой вершине будет сопоставляться номер ее доли (1 или 2). Если пытаемся из вершины v пойти в вершину, которая имеет ту же долю, что и v, то граф не двудольный.

Проверка на ацикличность: нужен дополнительный массив col, в котором каждой вершине будет сопоставляться цвет: белая 0 – не посещённая, серая 1 – посещенная и посещаются ее потомки, черная 2 – посещенная вместе со своими потомками. При попытке пойти в серую вершину (в которую уже ходили и пытаемся попасть в неее из ее потомка) обнаруживается цикл.

Построение стягивающего дерева: Для произвольного неориентирован­ного графа G = <V, Е> каждое дерево <V, Т>, где Т ∈ Е, будем назы­вать стягивающим деревом или каркасом графа G. Нужно, чтобы все вершины были в этом дереве, значит каждую не посещённую вершину нужно обязательно добавить инцидентное ей ребро.

Топологическая сортировка:

• порядок вершин, при котором каждая дуга ведет из вершины, которая была раньше в порядке, в вершину, которая позже

• существует, если граф ацикличен

• алгоритм:

  1. произведем серию dfs (запускаем dfs из каждой не посещённой вершины), к моменту выхода из вызова    все вершины, достижимые из 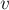 уже посещены обходом. Следовательно, если мы будем в момент выхода из   добавлять нашу вершину в начало некоего списка, то в конце концов в этом списке получится топологическая сортировка.

  2. перепишем ответ в обратном порядке

10. Понятие дерева. Свойства деревьев.

Дерево – простой связный граф без циклов. Простой (не обязательно связный) граф без циклов называется лесом.

Вершина дерева, имеющая степень 1, называется листом.

Лемма. У любого дерева, построенного на n≥2 вершинах, имеется как минимум 2 листа.

Доказательство. Рассмотрим произвольный простой путь Р = (х1,х2,..., хк) максимальной длины. Его концы – листья. Предположим, что один из концов (пусть хк) – не лист. Тогда он либо связан с еще одной вершиной хк-1, что противоречит условию максимального пути х1-хк, либо связан с вершиной хi (i<k), но тогда получается цикл, что противоречит условию дерева.

Теорема. В дереве, построенном на n вершинах, имеется ровно n-1 ребро.

Доказательство по индукции.

Обратная теорема. Любой простой связный граф, построенный на n вершинах и имеющий n-1 ребро, является деревом.

Доказательство от противного. Существует цикл С. Любое ребро е, принадлежащее циклу С, мостом в графе G не является. Удаляем по очереди ребра из циклов, пока они есть, получаем простой связный граф без циклов, то есть дерево. По предыдущей теореме у него n-1 вершина.

Следствие. Всякий связный граф, построенный на n вершинах, имеет как минимум n-1 ребро.

По-другому это означает, что у всякого связного графа существует остовное дерево.

• Связный граф является деревом тогда и только тогда, когда любое его ребро является мостом.

• Граф является деревом тогда и только тогда, когда для любых его вершин существует единственный простой путь, соединяющий эти вершины.

•Следствие. Пусть T есть остовное дерево связного графа G, и пусть e – ребро, не принадлежащее T. Тогда граф T+e содержит единственный цикл, который проходит через e.

Корневым деревом называется дерево с выделенной вершиной, называемой корнем. Корневым лесом называется лес, каждая компонента связного которого представляет собой корневое дерево.

m-арное дерево (например, бинарное)

11. Помеченные деревья. Теорема Кэли.

Теорема (формула Кэли). Количество a_n различных помеченных деревьев на n вершинах равно n^n-2. Доказательство (Х.Прюфер, 1918 г.).

Код Прюфера или последовательность Прюфера переводит помеченные деревья порядка n в последовательности чисел по следующему алгоритму:

1. Выбирается лист с минимальным номером.

2. Лист и инцидентное ему ребро удаляются из дерева, а в последовательность Прюфера добавляется номер смежной с данным листом вершины.

3. Если в дереве больше двух вершин, то п. 1, иначе — выход.

По любому коду Прюфера можно однозначно восстановить исходное дерево.

Заметим:

1. Листья исходного дерева в коде не встречаются

2. Если вершина имеет степень k > 1, то такая вершина встречается в коде Прюфера ровно k-1 раз

3. Мы можем восстановить дерево, если на каждом шаге имели пару вершин – смежную и удаляемую. У нас есть последовательность смежных удаляемым вершин. Нужно восстановить по ней последовательность удаляемых.