Вопросы к экзамену (теоретическому зачету)

«Теория графов»

ФИиИТ, ПИ, МОиАИС

Оглавление

Поиск кратчайших путей во взвешенном графе. Основные понятия. Постановка задачи. Алгоритм Дейкстры, алгоритм Флойда, алгоритм Форда-Беллмана. Примеры. 11

1. История возникновения и развития теории графов. Задача о кенигсбергских мостах, головоломка Гамильтона, задача о четырех красках, задачи связанные с химией и физикой.

З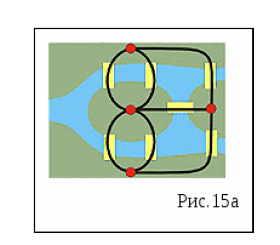 адача о семи мостах Кенигсберга. 1736 год. В письме Эйлер пишет о том, что он смог найти правило, пользуясь которым легко определить, можно ли пройти по всем мостам, не проходя дважды ни по одному из них (в случае семи мостов Кёнигсберга это невозможно).

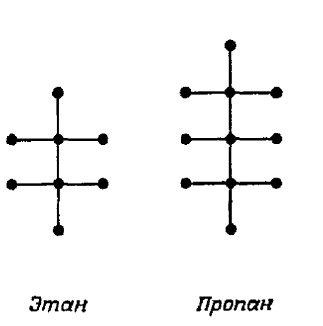
Задачи органической химии: Перечислить число предельных углеводородов с данным числом n атомов углерода. На языке графов: найти число всех деревьев с заданным количеством вершин и со степенями вершин 1 и 4

Теория графов для исследования электрических цепей 1847 год Физик Густав Роберт Кирхгоф Множество фундаментальных циклов в графе

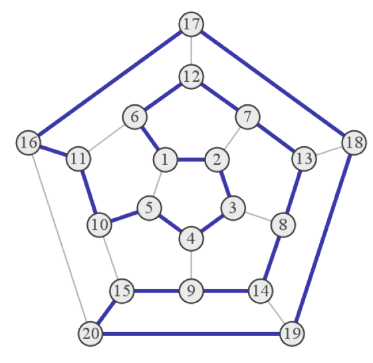
Головоломка Гамильтона «Вокруг света» : Обойти «вокруг света» по ребрам многогранника, посещая каждую вершину ровно один раз.

Задача коммивояжера— задача, в которой коммивояжер должен посетить N городов, побывав в каждом из них ровно по одному разу и завершив путешествие в том городе, с которого он начал.

Задача о раскраске карт или гипотеза о четырех красках

1850-1852 г.г. (приблизительно) Ф.Гатри постановка задачи: «сколько потребуется красок для раскраски любой плоской карты таким образом, чтобы никакие две смежные области не были окрашены в один и тот же цвет». Гипотеза: достаточно четырех красок.

1890 г. лектор Дурхэмского университета Перси Джон Хивуд опровергнул доказательство Кемпе и показал, что гипотеза верна для пяти красок.

В июне 1976 года, затратив 1200 часов машинного времени, Хакен и Аппель заявили, что им удалось проанализировать все 1482 карты и для раскрашивания ни одной из них не требуется более четырех красок.

2. Прикладные задачи теории графов. Веб-граф, графы социальных сетей, кластеризация и др. задачи. Графы де Брейна и биоинформатика. Деревья решений. Графы дорог. Графы и автоматы.

З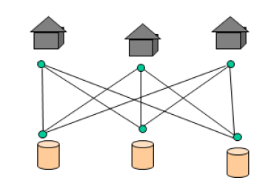 адача о домиках и колодцах. Три поссорившихся соседа имеют три общих колодца. Можно ли провести непересекающиеся дорожки от каждого дома к каждому колодцу?

Математическая модель интернета – веб-граф (А.Райгородский). Вершинами этого графа будут сайты, и между двумя вершинами A, B мы проведем столько ребер, направленных от A к B, сколько есть ссылок с сайта A на сайт B, и столько ребер, направленных от B к A, сколько есть ссылок с сайта B на сайт A.

Свойства веб-графа:

•Диаметр веб-графа равен 6 (закон шести рукопожатий)

•Веб-граф является достаточно разреженным: если вершин у веб-графа n, то ребер у него не более mn с некоторым постоянным m ≥ 1

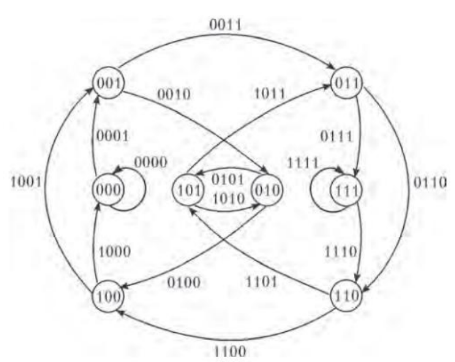
Теория графов и реконструкция генома. Граф де Брейна: Алфавит из n букв, число l. Вершины – все возможные слова длины l-1. Ребро из вершины x в вершину y строится тогда, когда существует l-буквенное слово, для которого x является префиксом, y – суффиксом. Все графы де Брейна имеют эйлеров цикл.

Граф дорог – это цифровая векторная карта, состоящая из топологически связанных дуг и узлов, местоположение и свойства которых с заданной точностью и полнотой передают маршруты и организацию движения наземного транспорта.

Метод деревьев решений является одним из наиболее популярных методов решения задач классификации и прогнозирования.

Анализ больших данных. Поиск сообществ в графах. Задачи кластеризации. Выделение сообществ (кластеров) разных объектов: пользователей, сайтов, продуктовых страниц интернет-магазинов:

1.Выделение сегментов пользователей для проведения рекламных кампаний.

2.Использование кластеров в качестве предикторов в персональных рекомендациях

3.Снижение размерности в любой задаче машинного обучения.

4.Сличение товарных URL между различными интернет-магазинами с целью выявления среди них групп, соответствующих одному и тому же товару.

5.Компактная визуализация — человеку будет проще воспринимать структуру данных.

3. Понятие графа, основные определения (вершины, ребра, дуги, ориентированные и неориентированные графы, простой граф, мультиграф, петли, кратные ребра). Виды графов: полный, двудольный, полный двудольный. Дополнение. Изоморфизм. Примеры.

Граф (простой) — пара G=(V, E), где V≠Ø – конечное множество вершин, E – множество пар вершин.

Если E — множество неупорядоченных пар вершин, то граф называется неориентированным (элементы множества E называют ребра), иначе — ориентированным (элементы множества E называют дуги).

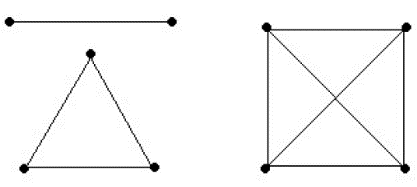Возможность кратных ребер и петель – мультиграф.

Граф называется полным, если каждая его вершина смежна со всеми остальными. Полный граф с n вершинами обозначается Kn.

Граф G=(V,E) называется двудольным, если множество его вершин можно разбить на два непересекающихся подмножества таким образом, что любое ребро будет иметь своими концами вершины из разных подмножеств.

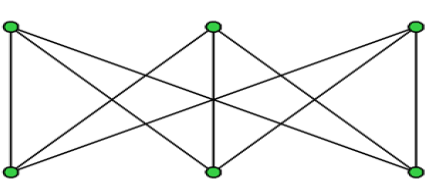
Д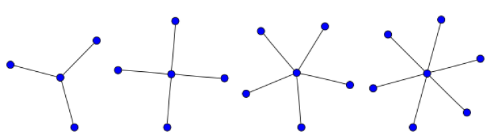 вудольный граф называется полным, если каждая вершина из V1 соединена ребром с каждой вершиной из V2. Полный двудольный граф обозначается Km,n.

Граф Kn,1 называется звездой.

Дополнением графа G называется граф, у которого множество вершин совпадает со множеством вершин графа G, а множество ребер дополняет множество ребер графа G до полного графа. Дополнением полного графа является пустой граф, то есть граф, все вершины которого изолированные.

Два графа (V1,E1) и (V2, E2) называются изоморфными, если существует биекция (взаимно-однозначное соответствие) f: V1→V2, такая что (u, v) ϵ E1 тогда и только тогда, когда (f(u), f(v)) ϵ E2. (можно сказать, что взяли два одинаковых графа и переименовали вершины)

4. Степени вершин, теорема Эйлера. Примеры (количество ребер в полном и полном двудольном графах).

•В неориентированном графе степенью deg(x) или валентностью вершины x называется количество ребер, инцидентных x (т.е. все ребра для неорграфа, входящие и исходящие дуги для орграфа).

•Если вершина имеет степень 0, то она называется изолированной.

•В орграфе различают входящую (indeg(x)) и исходящую (outdeg(x)) степень вершины.

Теорема Эйлера, 1737 год.

1. В графе сумма степеней вершин равна удвоенному числу ребер (лемма о рукопожатиях);

2. Число вершин нечетной степени четно;

3. Найдется по крайней мере две вершины, имеющие одинаковую степень.

Док-во.

1. При подсчете степеней вершин каждое ребро встречается два раза, т.к. два конца у каждого ребра.

2. 

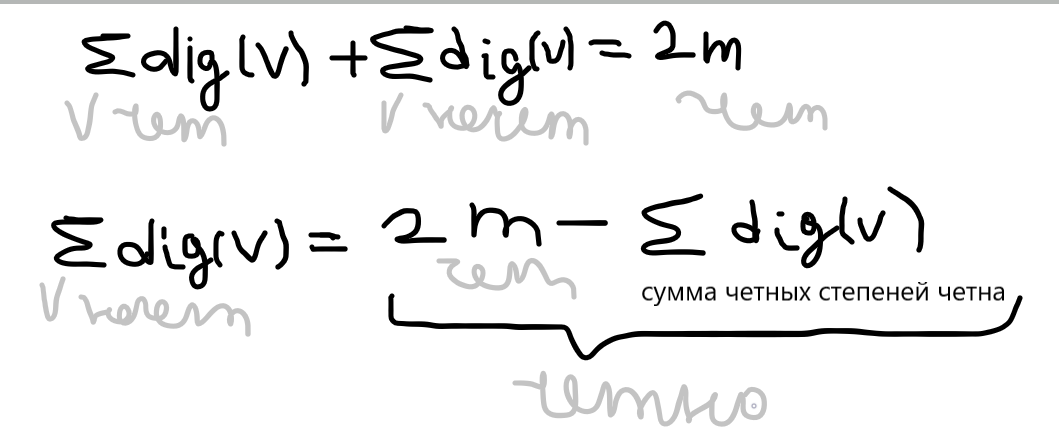
3. Теоретически степени вершин в графе с n вершинами могут принимать значение от 0 до n-1. Но 0 и n-1 не могут быть одновременно, следовательно на n вершин остается n-1 вариант выбора степени для n вершин.

•В полном графе с n вершинами - n(n-1)/2 ребер.

•В полном двудольном графе Km,n количество ребер – nm.

•В двудольном графе сумма степеней вершин одной доли равна сумме степеней вершин второй доли.

5. Маршруты, пути, цепи, циклы. Связность, компоненты связности. Расстояние, диаметр, эксцентриситет, центр. Примеры.

Маршрутом в графе G из вершины x0 в вершину xk называется последовательность

x0,e1,x1,e2,x2,...,xk-1,ek,xk вершин xi ϵ V и ребер ei ϵ E, где ei = (xi-1,xi). И вершины, и ребра в такой последовательности могут повторяться. Количество ребер в маршруте называется длиной маршрута.

Если все ребра в маршруте различны, то такой маршрут называется путем из вершины x0 в вершину xk.

Если также и все вершины в данном пути различны, то такой путь называется простым (цепью).

Замкнутым путем называется путь, в котором начальная и конечная вершина совпадают. Циклом называю замкнутый простой путь.

Если две вершины графа соединены хотя бы одним путем, то такие вершины называются связанными.

Связанность задает отношение эквивалентности на множестве вершин графа. Это отношение делит граф на классы эквивалентности, которые называются компонентами связности графа.

Если в графе существует лишь одна компонента связности, то есть, любые две вершины соединены хотя бы одним путем, то такой граф называется связным.

Расстоянием d(x,y) между двумя связанными вершинами x,y называется длина наименьшего пути между ними (понятно, что такой путь обязательно является простым). В том случае, когда вершины не являются связанными, полагают, что d(x,y)= ∞.

Диаметром графа diam(G) называется максимальное расстояние между его вершинами. В случае несвязного графа полагают, что diam(G) = ∞.

Эксцентриситетом вершины называется максимальное расстояние от нее до любой вершины графа.

Радиусом графа r(G) называется минимальный из эксцентриситетов вершин графа G, а вершины, на которых этот минимум достигается, называются центральными вершинами.

Множество всех центральных вершин называется центром графа.

6. Теорема Кенига. Примеры.

Теорема Кёнига. Граф G является двудольным тогда и только тогда, когда в нем отсутствуют циклы нечетной длины (нечетные циклы).

Док-во.

|=> граф G двудольный → Нет нечетных циклов.

Пусть граф двудольный. Тогда, если выйдем из произвольной вершины x ϵ V и захотим в нее вернуться, то нам придется сделать четное число шагов (за нечетное число шагов окажемся в другой доле), поэтому любой цикл имеет четную длину.

<=| Нет нечетных циклов → граф G двудольный.

Пусть в графе нет циклов нечетной длины и граф связен. Выберем вершину х. Разобьём вершины на два блока:

1. Блок Y: все вершины y, длина кратчайшего пути до которых от x нечетная

2. Блок X: остальные.

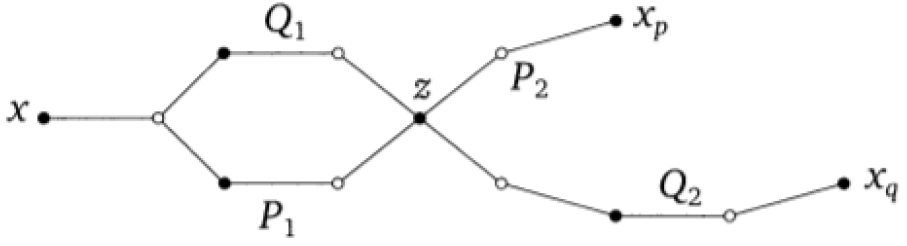
Докажем, что любые две вершины xp, xq ϵ X не являются смежными.

Рассмотрим произвольные кратчайшие пути, которые соединяют х с xp, xq. Обозначим z последнюю посещенную общую вершину этих путей. Она разбивает каждый из этих подпутей на две части. Длины P1 и Q1 должны совпадать.

Т.к. xp, xq принадлежат блоку Х, то длины путей P и Q имеют одинаковую четность => P2 и Q2 имеют одинаковую четность и не имеют никаких других общих вершин, кроме z. Т.е. если будет существовать ребро (xp, xq), то будет противоречие. Аналогично для блока Y.

7. Понятие связности для орграфов. Граф компонент сильной связности. Турнир.

Вершины x и y орграфа называются связанными, если существует хотя бы один путь из x в y и хотя бы один путь из y в x.

Отношение связанности – отношение эквивалентности. Классы эквивалентности – компоненты сильной связности. Орграф называется сильно связным, если он состоит из единственной компоненты сильной связности.

Турнир — это ориентированный граф, полученный из неориентированного полного графа путём назначения направления каждому ребру.

8. Подграф. Операции удаления вершин и ребер. Остовной подграф. Точки сочленения и мосты, их свойства.

Подграфом графа G называется граф H, для которого выполнены следующие условия:

1. V (H) ⊆ V (G); (некоторые вершины)

2. E(H) ⊆ E(G); (некоторые ребра)

3. Любое ребро e ∈ E(H), соединяющее пару вершин x и y в H, должно соединять ту же самую пару вершин в графе G.

Можно сказать, что любой подграф H графа G – это граф, полученный из исходного с помощью последовательного выполнения двух операций двух операций: удаления вершины и удаления ребра.

•Удаление ребра e

Множество вершин не меняется, из множества ребер удаляется элемент e. Полученный граф обозначается G-e. Можно сразу удалить несколько ребер, принадлежащих некоторому подмножеству S множества E. Полученный граф обозначается G-S.

•Удаление вершины x

Если эта вершина является изолированной, то кроме ее удаления ничего больше делать не нужно. Если же этой вершине инцидентны какие-то ребра, то будем также вместе с вершиной x удалять и их. Полученный в результате удаления вершины x граф обозначается обычно G−x.

В более общем случае мы с помощью операции удаления вершин из подмножества S ∈ V(G) получаем подграф G−S, в котором по сравнению с исходным графом G удалены все вершины подмножества S вместе со всеми ребрами, инцидентными этим вершинам.

Если мы при получении из графа G подграфа H используем лишь операцию удаления ребер, то мы получаем подграф, множество вершин которого совпадает с множеством V вершин исходного графа. Такой подграф называется остовным подграфом (spanning subgraph) графа G. В частности, любой простой граф G, построенный на n вершинах, является остовным подграфом полного графа Kn.

Подграфом H графа G, индуцированным подмножеством вершин S, называется граф, полученный из G удалением всех вершин, не принадлежащих множеству S, вместе со всеми инцидентными этим вершинам ребрами.