
Лабораторные работы / msu_lab1
.pdf
Отчет по лабораторной работе № 1 по дисциплине «Моделирование систем управления»
на тему:
«Исследование методов моделирования динамических систем на базе аналоговых структурных моделей»
Цель работы
Закрепить знания по исследованию методов аналогового структурно моделирования на примере динамических объектов первого и второго порядков, а также освоить инструментальную базу моделирования непрерывных систем в среде MATLAB/Simulink.
Выполнение работы:
1. Исследование структурной модели динамического звена первого порядка с уравнением связи:
где y(t) и u(t) – сигналы на выходе и входе объекта соответственно.
Исходные данные: k = 2,0; T1 = 1,0; T2 = 0,15.
1.1. Получение структурной аналоговой модели динамического звена для заданного варианта параметров объекта.
Перегруппируем слагаемые в исходном уравнении так, чтобы слева были производные, справа – сигналы:
Структурная аналоговая схема, соответствующая полученному уравнению, представлена на рис.1.1.
Рисунок 1.1
1.2. Реализация модели на базе средств MATLAB/Simulink.
Модель, собранная в Simulink, представлена на рис.1.2.
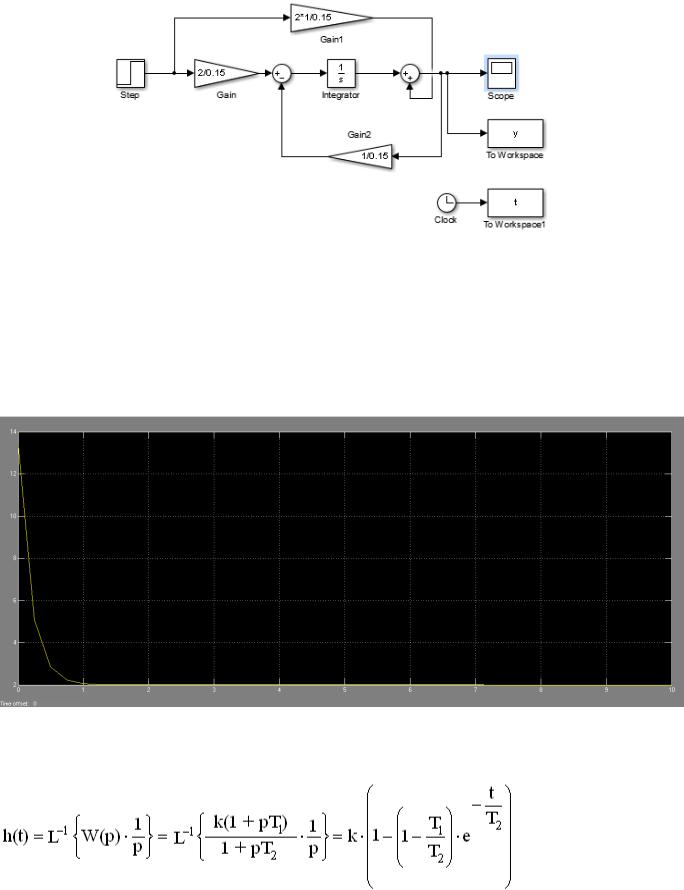
Рисунок 1.2
1.3. Исследование влияния величины шага t интегрирования уравнений состояния системы на точность расчета переходной функции. Используемый метод интегрирования – Рунге–Кутты с фиксированным шагом.
Переходная характеристика динамического звена при шаге интегрирования t = 0,25 с представлена на рис.1.3.1.
Рисунок 1.3.1
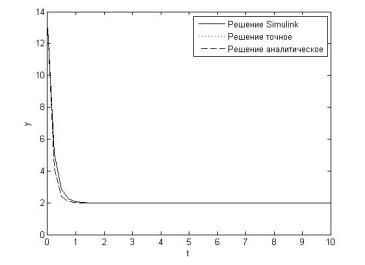
Получим аналитическое выражение для переходной функции динамического звена:
С учетом заданных параметров:
h(t) = 2 × (1 – (1 – 1/0,15) × e-t/0,15) = 2 × (1 + 5,67 × e-6,67t)
2
Содержание блока пользователя с функцией вычисления переходной характеристики системы на основе аналитического выражения с вычислением отклонения переходной функции, получаемой на выходе модели, от аналитически рассчитанной на интервале [0÷tуст] представлено ниже:
%Переменная Лапласа p=tf('p');
%Передаточная функция
W=2*(1+p)/(1+0.15*p);
%Решение точное
[y1,t1]=step(W,t);
%Аналитически полученная переходная функция y2=2*(1+5.67*exp(-6.67*t));
%Вывод графика y=y(:,1);
plot(t,y,'-k',t1,y1,':k',t,y2,'--k'); xlabel('t');
ylabel('y');
legend('Решение Simulink','Решение точное','Решение аналитическое');
%Разность решений Simulink и точного
e=y-y1;
% Скреднеквадратическое отклонение fprintf('Отклонение: %g\n',sum(e.^2)/length(e));
Графики переходных функций, полученных с помощью построенной модели, встроенной в MATLAB функции и аналитически полученной функции при шаге интегрирования t = 0,25 с представлены на рис.1.3.2.
Рисунок 1.3.2.
Из рис.1.3.2 видно, что аналитическое решение немного отличается от точного решения и решения Simulink.
Путем изменения величины шага интегрирования в пределах диапазона [0,05÷2,05]*T1 определим для каждого значения t ошибку моделирования переходного процесса системы. Результаты моделирования представлены в таблице 1.
3
|
Таблица 1 |
t, с |
δинт |
0,05 |
8,85496×10-9 |
0,07 |
1,63907×10-7 |
0,10 |
3,92314×10-6 |
0,15 |
0,000172676 |
0,17 |
0,000579015 |
0,20 |
0,0028213 |
0,25 |
0,0269466 |
0,30 |
0,185759 |
0,35 |
1,11417 |
0,40 |
10,8251 |
Прекратим увеличивать шаг интегрирования для вычисления ошибки после получения большого значения ошибки при t = 0,40.
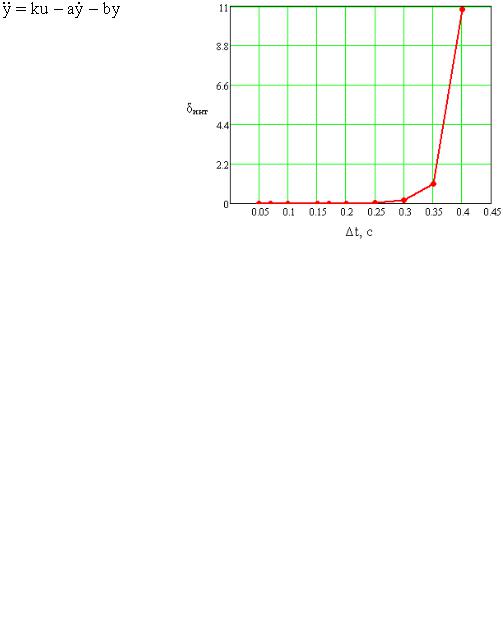
График зависимости ошибки от величины шага интегрирования представлен на рис.1.3.3.
Рисунок 1.3.3
Из таблицы 1 и рис.1.3.3 видно, что при увеличении шага интегрирования отклонение переходной функции, получаемой на выходе модели, от переходной функции, полученной с помощью встроенной в MATLAB функции увеличивается.
2. Исследование структурной модели колебательного звена, заданного в форме дифференциального уравнения связи:
Исходные данные: a = 0,8; b = 3,0; k = 6,0.
2.1. Составление аналоговой схемы моделирования для заданного варианта параметров колебательной системы.
Перегруппируем слагаемые в исходном уравнении так, чтобы слева были старшие производные, справа – все остальное:
4
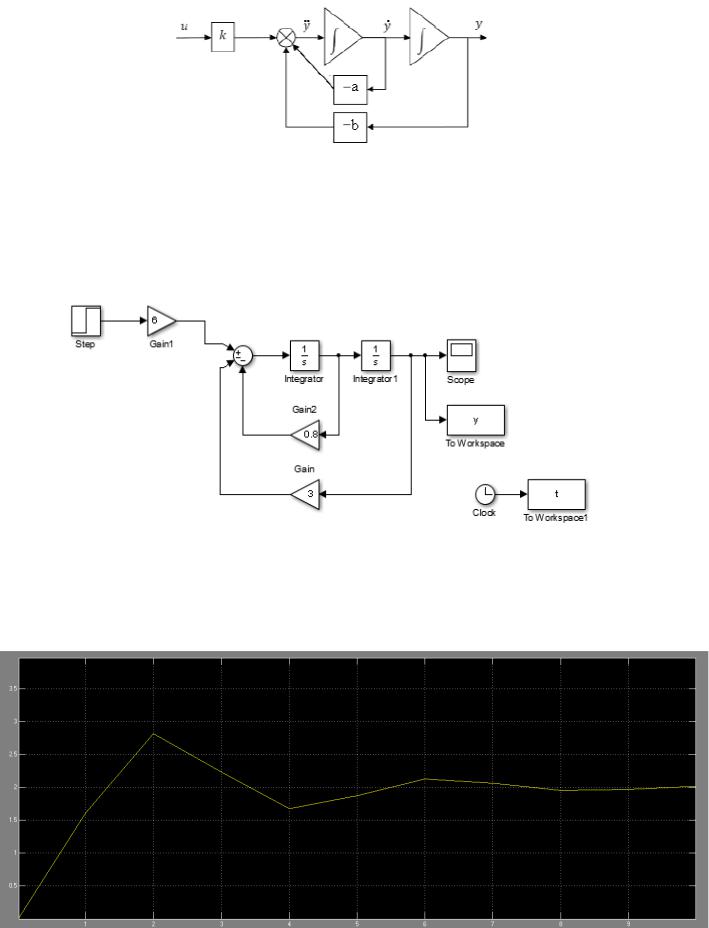
Структурная аналоговая схема, соответствующая полученному уравнению, представлена на рис.2.1.
Рисунок 2.1
2.2. Реализация модели системы на базе пакета MATLAB/Simulink.
Модель, собранная в Simulink, представлена на рис.2.2.1.
Рисунок 2.2.1
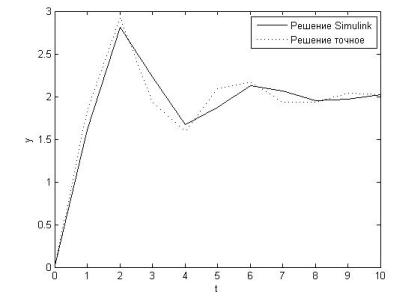
Переходная характеристика колебательного звена при шаге интегрирования t = 1 с представлена на рис.2.2.2.
Рисунок 2.2.2
5
2.3. Исследование влияния величины шага интегрирования t уравнений состояния системы на точность расчета переходной функции и построение графика зависимости ошибки моделирования переходной функции системы от величины шага интегрирования.
Содержание блока пользователя с вычислением отклонения переходной функции, получаемой на выходе модели, от переходной функции, полученной с помощью встроенной в MATLAB функции, на интервале [0÷tуст] представлено ниже:
%Переменная Лапласа p=tf('p');
%Передаточная функция
W=6/(p*p+0.8*p+3);
%Решение точное
[y1,t1]=step(W,t);
%Вывод графика y=y(:,1); plot(t,y,'-k',t1,y1,':k'); xlabel('t'); ylabel('y');
legend('Решение Simulink','Решение точное');
%Разность решений Simulink и точного e=y-y1;
%Скреднеквадратическое отклонение
fprintf('Отклонение: %g\n',sum(e.^2)/length(e));
Графики переходных функций, полученных с помощью построенной модели и встроенной в MATLAB функции при шаге интегрирования t = 0,25 с представлены на рис.2.3.1.
Рисунок 2.3.1
Из рис.2.3.1 видно, что точное решение немного отличается от решения Simulink.
Путем изменения величины шага интегрирования определим для каждого значения t ошибку моделирования переходного процесса системы. Результаты моделирования представлены в таблице 2.
6
|
Таблица 2 |
t, с |
δинт |
0,05 |
5,47073×10-13 |
0,10 |
1,4419×10-10 |
0,15 |
3,83691×10-9 |
0,20 |
3,91402×10-8 |
0,30 |
1,07361×10-6 |
0,50 |
7,1768×10-5 |
1,00 |
0,0209594 |
1,30 |
0,135293 |
1,50 |
0,420161 |
1,70 |
5,19739 |
Прекратим увеличивать шаг интегрирования для вычисления ошибки после получения большого значения ошибки при t = 1,70.
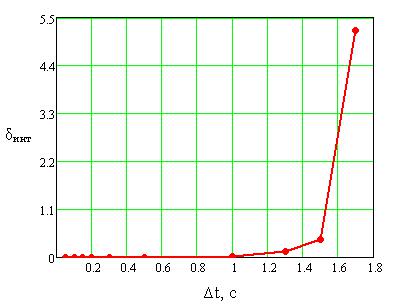
График зависимости ошибки от величины шага интегрирования представлен на рис.2.3.1.
Рисунок 2.3.1
Из таблицы 2 и рис.2.3.1 видно, что при увеличении шага интегрирования отклонение переходной функции, получаемой на выходе модели, от переходной функции, полученной с помощью встроенной в MATLAB функции увеличивается.
7
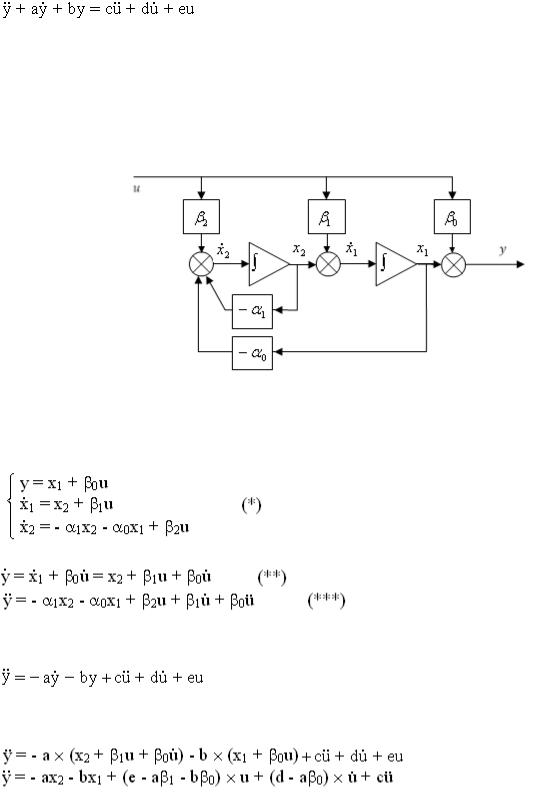
3. Моделирование системы с дифференциальным оператором второго порядка по выходной и входной переменным.
Исходные данные: a = 1,8; b = 5,0; c = 1,1; d = 3,9; e = 4,0.
3.1. Построение структурной аналоговой модели по заданному варианту параметров
объекта.
Структурная аналоговая схема представлена на рис.3.1.
Рисунок 3.1
Найдем соответствие между параметрами исходного дифференциального уравнения и параметрами структурной схемы на рис.3.1.
Перепишем исходное уравнение:
С учетом (*) и (**) запишем:
Сравнивая последнее уравнение с (***), имеем:
α1 = a = 1,8 α0 = b = 5 β0 = c = 1,1
β1 = d - aβ0 = 3,9 – 1,8 × 1,1 = 1,92
β2 = e - aβ1 - bβ0 = 4 - 1,8 × 1,92 - 5 × 1,1 = - 4,956
8
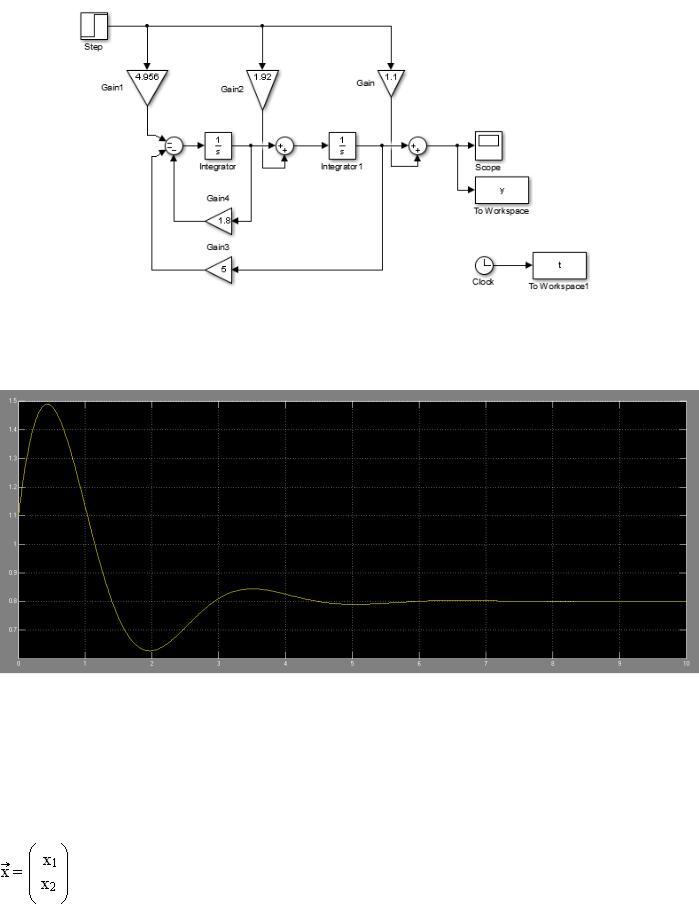
3.2. Получение графика переходного процесса на выходе системы при подаче на вход сигнала ступенчатой формы.
Модель, собранная в Simulink, представлена на рис.3.2.1.
Рисунок 3.2.1
График переходного процесса на выходе системы при подаче на вход сигнала ступенчатой формы представлен на рис.3.2.2.
Рисунок 3.2.2
3.3. Получение математической модели исследуемого объекта в пространстве состояний в стандартной форме на основе построенной ранее аналоговой модели. Реализация модели в среде MATLAB/Simulink при подаче на вход сигнала ступенчатой формы. Сравнение результатов моделирования с полученными в п. 3.2.
Обозначим вектор переменных состояния:
9
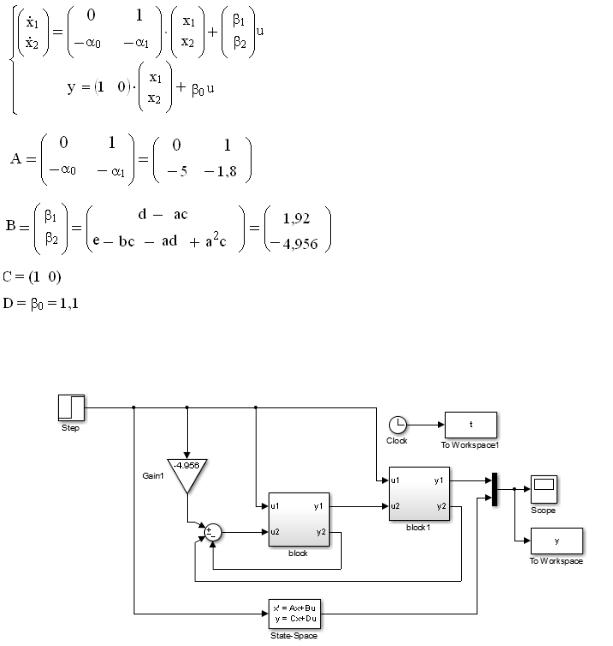
Уравнения состояния линейной динамической системы запишем в матричной форме:
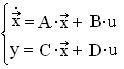 ,
,
где A, B, C, D - матрицы состояния, управления, наблюдения и связи вход-выход соответственно.
Сравнивая данную систему уравнений с (*), получаем:
Модель, собранная в Simulink, представлена на рис.3.3.1.
Рисунок 3.3.1
10
