Попов П.М., Попов С.П., 2001 - Верификационные методы анализа оптимального управления процессами и системами

5.4. Оптимизация параметров ЭСУД при их изменении

Найдём соотношение между параметрами В, Е, U и W при условии, что их изменение приводит к наиболее быстрому возрастанию величины (5.35), то есть максимально быстро увеличивается сложность ЭСУД и её потенциальные возможности. В этом смысле при таком изменении параметров развитие ЭСУД оптимально, и оно определяется направлениями градиентов к поверхно-

145

6. ОПТИМИЗАЦИЯ ПАРАМЕТРОВ ИЗМЕНЕНИЯ ТЕХНИЧЕСКОГО СОСТОЯНИЯ ЭЛЕКТРОННЫХ СИСТЕМ УПРАВЛЕНИЯ ДВИГАТЕЛЯМИ

Рассмотрим процедуру оптимизации параметров технического состояния ЭСУД уже по известным методам классической высшей математики, таких как теория массового обслуживания, теория игр и решений, теории вероятности, теории информации и других методов оптимизации [50].

Например, оптимизацию технического состояния агрегатов и узлов ЭСУД в составе системы - «Автомобиль» обеспечивают не только за счет режима работы подсистем и узлов в заданных эксплутационных условиях, но и на основе обоснования пробега автомобиля с ЭСУД до предельного состояния и минимальных суммарных затрат на поддержание работоспособности системы в этих условиях. Определить оптимальное [50,52] значение оставшегося пробега автомобиля с ЭСУД до предельного состояния подсистем агрегатов и узлов можно прогнозированием, статистическими методами прогнозирования

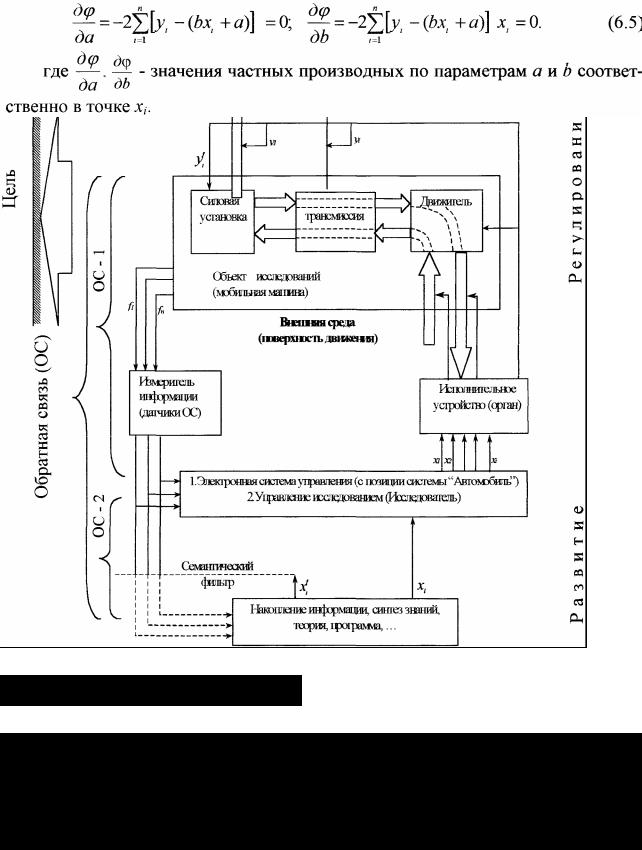
наблюдений и другими экономико-математическими и технико-экономическими методами анализа ЭСУД в составе системы — «Автомобиль» равно как и других технических систем. Качество прогнозирования, уровень его достоверности и точности, уровень затрат на получение прогноза от выбранного метода прогнозирования, принятой математической модели, числа данных и методики определения параметров принятой зависимости. Поэтому необходимо знать основные положения методики определения зависимости. Модель исследования механизма ЭСУД в составе системы — «Автомобиль» представлена на рис. 6.1.

6.1. Определение параметров распределения и линейной оптимизации ЭСУД в составе системы «Автомобиль»

Для практического использования известных или полученных зависимостей необходимо определить численные значения параметров. Наиболее просто определить параметры плотности распределения случайной величины, коэффициенты корреляции [40,42,43,44,45] и корреляционного отношения [42]; более сложно определить параметры линейной параболической зависимости по способу

наименьших квадратов; степенные и экспоненциальные зависимости сводятся чаще всего к линейной зависимости математическими преобразованиями.

При известном виде распределения определяют математическое ожидание и дисперсию. Значение параметра, вычисленное на основе ограниченного числа опытов, всегда содержит элемент случайности. Определенные таким образом значения параметров следует называть оценкой.

147

Чтобы найти значения а и Ь, при которых левая часть этого выражения будет минимальная, продифференцируем функцию по а и Ъ и приравняем производную к нулю: