1. Элементарные и сложные случайные события и операции над ними. Свойства операций.

Элементарные события (исходы) – такие случайные события, одно из которых должно обязательно произойти в данном опыте, и они не происходят одновременно.

Например, у игральной кости 6 элементарных исходов (1, 2, 3, 4, 5, 6).

Сложное событие – событие, состоящее из нескольких элементарных.

Например, при подбрасывании игральной кости выпало число очков, кратное трём. Это значит, что произошло одно из двух событий: либо выпала тройка, либо шестёрка, т.е. событие – число очков кратное трём – сложное событие, которое можно разложить на два элементарных.

Суммой событий А и В называется событие С = А + В, состоящее в наступлении хотя бы одного из них.

Произведением событий А и В называется событие С = А * В, состоящее в совместном наступлении этих событий.

Разностью событий А и В называется событие С = А – В, происходящее только тогда, когда происходит событие А, но не происходит событие В.

Противоположным событию А называют событие А (с чертой), которое происходит тогда и только тогда, когда не происходит А.

С обытие А влечёт событие, если из того, что происходит событие А следует, что происходит событие В.

Свойства операций над событиями:

A + B = B + A A*B = B*A – переместительное

(А + В)*С = А*С + В*С – распределительное

(А + В) + С = А + (В + С) (А*В)*С = А*(В*С) – сочетательное

А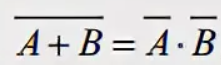 + А = А А*А = А

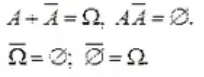
2. Классическое определение вероятности события: конечное число равновозможных элементарных исходов.

Вероятностью события называется отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу.

Несовместными называют такие события, которые не могут произойти одновременно.

Полная группа элементарных исходов образуется, если события попарно несовместны и в результате испытания происходит только одно из этих событий.

Пусть в такой схеме есть n – общее число равновозможных элементарных исходов, тогда для любого события А  Р(А) = m/n, где m – число благоприятствующих исходов.

3. Общее определение вероятности события (понятие о вероятностном пространстве).

4. Условная вероятность. Зависимые и независимые события.

Условной вероятностью называется вероятность события В, вычисленная в предположении, что событие А уже наступило.

События являются независимыми, если вероятность наступления любого из них не зависит от появления остальных событий рассматриваемого множества событий. Событие В называется зависимым, если вероятность P(B) зависит от появления или непоявления события А. Вероятность события В, вычисленная в предположении того, что событие А уже произошло, называется условной вероятностью наступления события В.

5. Основные вычислительные формулы теории вероятности: вероятность противоположного события, вероятность объединения событий, вероятность пересечения событий, формула полной вероятности, формула Байеса.

Событие, которое происходит тогда и только тогда, когда не происходит событие А, называется противоположным событию А и обозначается А (с чертой).

Если события А и В пересекаются, т.е. совместны, то вероятность их объединения можно найти по формуле:

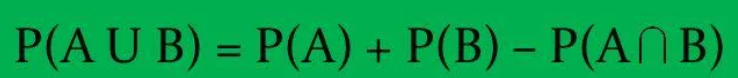
События называются совместными, если появление одного из них не исключает появления другого в одном и том же испытании.

6. Основные типы случайных величин (дискретные, непрерывные и смешанные) и способы их описания (функция распределения, ряд распределения, плотность вероятности, производящие и характеристические функции).

Случайной величиной (СВ) называется величина, которая в результате испытания может принять разные числовые значения в зависимости от случая. Случайные величины обозначаются заглавными буквами X, Y, а принимаемые ими значения – соответствующими строчными буквами x, y.

Соотношение, устанавливающее связь между возможными значениями случайной величины и их вероятностями, называется законом распределения случайной величины.

Пусть X – случайная величина, а x – произвольное число. Тогда вероятность того, что X примет значение, меньшее, чем х, называется функцией распределения данной случайной величины.

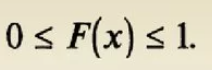
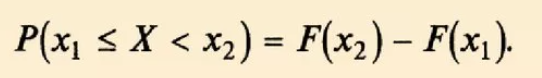
Ряд распределения – совокупность всех возможных значений x_i дискретной СВ Х и соответствующих им вероятностей p_i.

Плотность распределения вероятностей (только для непрерывных СВ) – первая производная от функции распределения (функция распределения первообразная плотности).

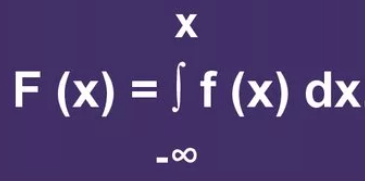
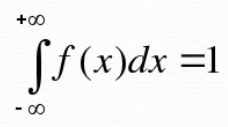
Дискретной случайной величиной (ДСВ) называется величина X, принимающая отдельные (изолированные) возможные значения x1, x2, …, x_n с вероятностями p1, p2, …, p_n соответственно. Под законом распределения ДСВ понимают зависимость вероятностей

p(X = x_k) того, что Х принимает значение х_k.

Непрерывными называются случайные величины, которые могут принимать все значения из некоторого числового промежутка. Пример: расстояние, которое пролетит снаряд при выстреле — это непрерывная случайная величина, значения которой принадлежат некоторому промежутку [а; b].

Вероятность того, что непрерывная случайная величина примет значение на интервале [а; b], равна интегралу от плотности распределения, взятому в пределах от а до b:

Случайная величина называется смешанной, если функция распределения F(x) на некоторых участках непрерывна, а в отдельных точках имеет разрывы (скачки).
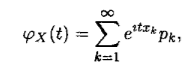
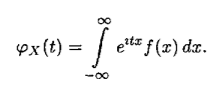