22) Движение тела переменной массы

В некоторых случаях тел связано с изменением их массы, например масса ракеты уменьшается вследствие истечения газов, образующихся при сгорании топлива, и т. п.  Произведем вывод уравнения движения тела переменной массы на примере движения ракеты. Если в момент времени t масса ракеты m, а ее скорость v, то по истечении времени dt ее масса уменьшится на dm и станет равной т-dm, а скорость станет равной v+dv. Изменение импульса системы за промежуток времени dt    где u - скорость истечения газов относительно ракеты. Тогда    здесь учтено, что dmdv - малое высшего порядка малости по сравнению с остальными слагаемыми. Если на систему действуют внешние силы, то dp=Fdt, поэтому    или  (1)  Второе слагаемое в правой части (1) называют реактивной силой F_p. Если u противоположен v по направлению, то ракета ускоряется, а если совпадает с v, то тормозится.  Таким образом, мы получили уравнение движения тела переменной массы  (2)  которое впервые было выведено И. В. Мещерским (1859-1935).  Рассмотрим случай отсутвтия воздействия внешних сил на ракету. Положим в уравнении (1) F=0 и будем считать, что скорость выбрасываемых газов относительно ракеты постоянна (ракета движется прямолинейно), получим    откуда    Значение постоянной интегрирования С определим из начальных условий. Если в начальный момент времени стартовая масса m₀, а ее скорость ракеты равна нулю, то С = uln(m0). Следовательно,    Это соотношение называется формулой Циолковского.  Выражения (2) и (3) верны для нерелятивистских движений, т. е. для случаев, когда скорости v и u малы по сравнению со скоростью света в вакууме.

23)   Рассмотрим движение частицы в стационарном поле .

Такое поле называется центрально-симметричным, или, коротко, центральным. В этом случае гамильтониан

коммутирует с оператором орбитального момента: Рассмотрим асимптотику ограниченного решения Атом водорода

.

Покажем это подробнее, получив следующее представление оператора квадрата импульса:

.

Имеем:

.

Из фундаментального соотношения следуют коммутаторы

,

используя которые, находим

.

Далеe:

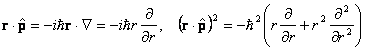
.В итоге получаем приведенное выше выражение для , откуда сразу видно, что .

24) Задача Кеплера вообще представляет собой проблему отыскания движения двух сферически-симметричных тел, взаимодействующих гравитационно. В классической теории тяготения решение этой проблемы было найдено самим Исааком Ньютоном: оказалось, что тела будут двигаться по коническим сечениям, в зависимости от начальных условий — по эллипсам, параболам или гиперболам. В рамках общей теории относительности с пуристической точки зрения эта задача представляется плохо поставленной, так как модель абсолютно твёрдого тела не возможна в релятивистской физике (смотри Парадокс Белла, Твёрдость по Борну), а не абсолютно твёрдые тела не будут при взаимодействии сферически-симметричными. Другой подход включает переход к точечным телам, правомерный в ньютоновской физике, но вызывающий проблемы в ОТО. Помимо этого, кроме положений и скоростей тел необходимо задать также и начальное гравитационное поле (метрику) во всём пространстве — проблема начальных условий в ОТО. В силу указанных причин точного аналитического решения задачи Кеплера в ОТО не существует (аналогично задаче трёх тел в ньютоновской теории тяготения), но есть комплекс методов, позволяющих рассчитать поведение тел в рамках данной задачи с необходимой точностью: приближение пробного тела, постньютоновский формализм, численная ОТО. В статье часто и без напоминаний подразумевается, что гравитационное поле — это то же самое, что и пространство-время.