Методичні рекомендації до виконання лабораторної роботи ГЕОМЕТРИЧНІ ПЕРЕТВОРЕННЯ ЗОБРАЖЕНЬ

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ “ЛЬВІВСЬКА ПОЛІТЕХНІКА”

ГЕОМЕТРИЧНІ ПЕРЕТВОРЕННЯ ЗОБРАЖЕНЬ

МЕТОДИЧНІ ВКАЗІВКИ

до лабораторної роботи з дисципліни "Фотограмметрія та дистанційне зондування, частина 2"

для студентів базового напряму 080101 "Геодезія, картографія та землеустрій"

Затверджено на засіданні кафедри

фотограмметрії та геоінформатики. Протокол № 3 (565) від 20.02.2015 р.

Львів–2015

Геометричні перетворення зображень: Методичні вказівки до лабораторної роботи з дисципліни "Фотограмметрія та дистанційне зондування, частина 2" для студентів базового напряму 080101 "Геодезія, картографія та землеустрій", Львівська політехніка", -2015.–12с.

Відповідальний за випуск Дорожинський О.Л., д-р техн. наук, проф.

2

1.Загальні відомості

Вході фотограмметричного опрацювання зображень виникає необхідність різного роду їх перетворень, пов’язаних як з покращенням читабельності, так і зміною розмірів зображення (наприклад, при масштабуванні зображень в процесі їхнього трансформування). В першому випадку говорять про фотометричну корекцію (оптичних перетвореннях) цифрового зображення, а в другому – про зміну його геометричного розрізнення та положення окремих елементів зображення, або про

геометричні перетворення.

Геометричні перетворення растрового зображення змінюють його площину і виконуються при трансформуванні цифрового знімка за елементами зовнішнього орієнтування, в процесі якого змінюється масштаб зображення і положення його елементів відносно координатних осей. Схожа задача виникає при внутрішньому орієнтуванні цифрового зображення та при взаємному співставленні між собою зображень. Часто (наприклад в задачах моніторингу) співставляють знімки однієї і тієї ж території, отримані в різний час, з різних точок простору і навіть з допомогою різних знімальних систем. Для коректного співставлення зображень необхідно виконати деяку їх попередню обробку з метою приведення знімків до геометрії, придатної для якісних вимірювань та інтерпритації.

Причинин виникнення геометричних деформацій зображень, отримуваних фотографічними знімальними ситемами є багато. Наприклад, коли рухома камера фіксує яскравісний образ спостережуваного об’єкта (оптичну поверхню) в виді послідовних зображень, то цей образ від знімка до знімка деформується внаслідок перспективних спотворень і зміни положення камери. Геометрія відповідних деформацій моделюється проективними перетвореннями, які є доповненням відомих перетворень евклідової геометрії (пригадайте, що довжини і кути в проективній геометрії не зберігаються, а паралельні лінії можуть перетинатись).

Загалом геометричні перетворення умовно розділяють на прості, потребуючі зміни тільки геометричного розрізнення, і складні, в результаті яких відбувається зміна масштабу, поворот зображення а також нелінійні викривлення. При цьому формується нова матриця, елементам якої присвоюється атрибути (яскравість, колір) як функцію відповідного йому вхідного зображення. Складні перетворення виконуються при трансформуванні зображення, коли коефіцієнт збільшення різних його частин неодинаковий, або коли виконується розворот на деякий кут. Перша ситуація виникає при відтворенні, наприклад, сітки квадратів за її перспективою, а друга

–при внутрішньому орієнтуванні знімка.

Координати елемента створюваного зображення знаходять за координатами відповідного йому елемента (чи кількох елементів) вхідного зображення, підставляючи їх в потрібну формулу перетворення.

3

2.Зміст та обсяг роботи

Робота містить домашнє завдання та аудиторну роботу в лабораторії кафедри. На виконання лабораторної роботи навчалою програмою відводиться 8аудиторних годин та 6 годин самостійної роботи.

Мета самостійної роботи студента – вивчення теоретичного матеріалу, аналіз завдання лабораторної роботи та оформлення в зошитах звіту.

Послідовність виконання роботи наступна.

1.Вивчити положення даної методичної розробки, ознайомитись з рекомендованою для вивчення літературою.

2.Відповісти письмово на контрольні запитання.

3.Виконати індивідуальне завдання.

4.Проаналізувати результати лабораторної роботи, скласти та оформити звіт.

3.Контрольні запитання

1.Встановіть ієрархію геометричних перетворень згідно їх взаємної підлеглості.

2.Якою повинна бути формула афінного перетворення простору при необхідності збереження подібності фігур?

3.При яких умовах матриця повороту при евклідовому перетворенні стає одиничною?

4.Як називається геометричне перетворення на площині, яке передбачає зміну масштабіа вздовж осей?

5.Які з геометричних перетворень на площині зберігають паралельність прямих?

6.В яких випадках рекомендується застосовувати поліноміальну апроксимацію для опису геометричних деформацій?

7.Розрахуйте координати точок перетвореного зображення, якщо до точки з координатами (5,5) застосоване Евклідове перетворення з параметрами:

φ=90°, tx=ty=0.

8.Розрахуйте координати точок перетвореного зображення, якщо до точки з координатами (1,1) застосоване афінне перетворення з параметрами: масштабні коефіцієнти α=β=1,1 , кут розвороту φ=180°, параметри зсуву tx=

ty=15.

4.Список літератури

1.Дорожинський О.Л., Тукай Р. Фотограмметрія: Підручник.-Львів: Видавництво Національного університету «Львівська політехніка», 2008. – 332с.

2.Дорожинський О.Л. Аналітична та цифрова фотограмметрія: Навч. Посібник.-Львів: Видавництво Національного університету «Львівська політехніка», 2002. – 164 с.

4

3. Колб І.З. Фотограмметрія та дистанційне зондування, ч.2.: Конспект лекцій [текст].

МЕТОДИЧНІ ВКАЗІВКИ ДО ВИКОНАННЯ ЕКСПЕРИМЕНТАЛЬНОЇ ЧАСТИНИ ЛАБОРАТОРНОЇ РОБОТИ

5. Ознайомлення з програмою MathCAD

Програма MathCAD є математичним процесором. Ідеологія його використання аналогічна запису людиною дій на листі паперу – людина записує на листку зліва направо, зверху вниз математичні вирази та коментарі до них. В такому ж порядку відбувається обробка програмою записів. Синтаксис записів теж максимально наближений до звичної для людини форми. Наприклад, проста дія знаходження різниці між двома числами в програмі MathCAD виглядає так само як і на листі паперу: 256-47 . Після натискання кнопки «=» отримуєте на екрані результат розрахунку.

Аналогічно можна виконати практично довільної складності вираз з використанням арифметичних, тригонометричних, логічних, логарифмічних чи статистичних функцій. Порядок виконання дій можна регулювати дужками. Для редагування виразу слід встановити курсор в потрібне положення у вирізі (навколо виразу сформується прямокутна рамка) і з клавіатури чи вибором в меню внести (чи стерти) потрібний символ, число чи дію. Програма сама слідкує за заповненням всіх позицій у виразі і формально контролює синтаксис. Помилки у виразах підсвічуються червоним кольором.

Якщо є потреба використовувати власні змінні у виразах, то їх попередньо (тобто вище або лівіше від виразу) слід явно задати з допомогою кнопки «:». Тому порядок дій такий – задаємо ім’я змінної , натискаємо кнопку «:» і відразу вписуємо значення. Виводимо курсор за межі виразу. Наприклад, задамо змінні А та F , використаємо їх в рівнянні для розрахунку змінної С та відобразимо на екрані результат розрахунку.

Слід зауважити, що назви змінних, набрані великими і малими літерами не тотожні.

5

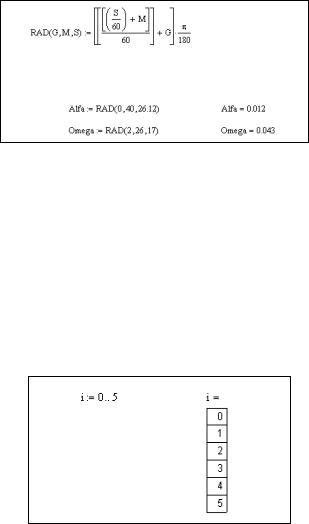
Практично за таким само принципом задаються матриці – задається і’мя, тиснемо кнопку «:», тиснемо кнопку , вибираємо розмір матриці та послідовно вводимо значення в кожну її позицію. Для стандартних дій над матрицями, таких як транспонування, обертання, знаходження визначників слід скористатись кнопками на панелі інструментів «Матриці».

Крім стандартних функцій, користувач може створювати і в довільному порядку використовувати й власні функції. Єдина умова – запис функції має передувати зверненням до неї. Наприклад, враховуючи, що програма працює з кутами, заданими в радіанах, а користувачу більш зручно задавати кути в градусній мірі, напишемо функцію, що переводить значення кута з градусів, мінут та секунд в радіани. Звертатись до цієї функції можна далі в програмі за її іменем і вказуючи формальні параметри:

Процесор MathCAD не має прямих можливостей для формування в програмі циклічних структур. Якщо виникає потреба організувати кількаразове звернення до якоїсь з частин програми при зміні параметрів її виконання (наприклад, виконати одну й ту ж дію з різними змінними), слід скористатись рядом. Тут «ряд» – це іменований список цілих значень, заданих в певному інтервалі з кроком 1. Наприклад, задамо ряд з іменем «і» в діапазоні від 0 до 5. Для цього слід скористатись кнопкою «;» при вказанні діапазону значень. Тому натискаємо: i , кнопка «:» , 0, кнопка «;», 5 . Результат видрукуємо кнопкою

«=»

Ім’я ряду можна використовувати як робочу змінну циклу або як індекс при звертанні до елементів рядів та матриць. Для того, щоб вказати індекс при змінній, скористайтесь кнопкою «[».

6

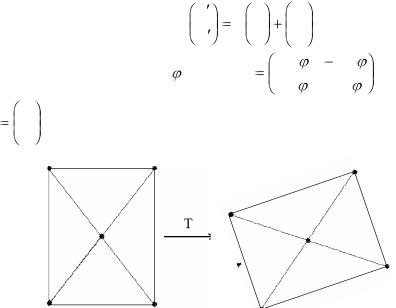
Лінійні перетворення можуть бути різного типу - починаючи від загального випадку довільних елементів матриці T і до спеціальних випадків, коли на елементи матриці накладаються ті чи інші обмеження. Слід відразу зазначити, що кожному лінійному перетворенню (чи руху) на площині завжди знайдеться обернене, що переводить точки в початкове положення, і будь-яким двом послідовно виконаним перетворенням точок площини відповідає деяке третє перетворення, здійснююче аналогічну за результатом операцію. Прийнято говорити, що множина всіх лінійних перетворень формує загальну лінійну групу. Серед множини загальних лінійних перетворень нас цікавлять лиш деякі підгрупи. Перш за все, ми розглянемо матриці перетворення, пов’язані з найбільш важливими підгрупами загальної лінійної (чи проективної) групи, а саме евклідову підгрупу, а також підгрупи подібності і афінну.

6.1. Евклідові перетворення

Сцену іноді можна розглядати як тверде тіло, коли взаємні деформації елементів сцени в тривимірному просторі не допускаються. Аналогічно і площину іноді можна вважати жорсткою (такою, що не деформується). Жорстким рухам площини відповідає евклідова підгрупа геометричних перетворень, яка містить лиш перетворення зсуву і повороту (рис.A.1), математично записуваних у векторно-матричній формі так:

Рис.A.1. Дія евклідового перетворення на п’ять точок площини (зсув, поворот).

відмітимо далі, що два послідовно проведені рухи площини можуть бути представлені єдиним рухом. Комбінація двох послідовних обертань R1 та R2

8

очевидно зводиться до обертання R1 R2 . Крім того, вибором обертання

та зсуву таке (друге) переміщення переводить точки площини в початкове положення. Матриці обертання R самі по собі формують так звану ортогональну підгрупу з важливою властивістю Rt R I , де І- одинична матриця.

Завдання 3: На основі програми з п.5 виконати пряме та обернене евклідове перетворення площини зображення. Привести аналіз дії програми на власний тестовий приклад.

6.2. Афінні перетворення

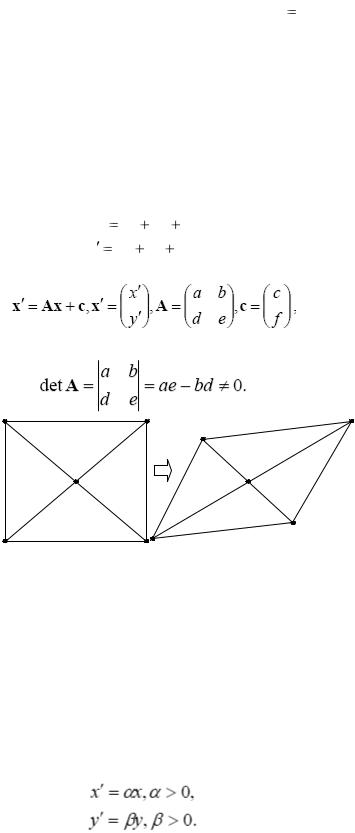
Якщо матрицю обертання в (A.2) замінити загальною невиродженою матрицею А , то отримаємо перетворення

x ax by c

або, в матричному виді

(A.6)

Зауважимо, що визначник матриці перетворення не дорівнює нулю:

Рис.A.2. Вхідне зображення (зліва) і його афінно-перетворена копія (праворуч). Параметри афінного перетворення: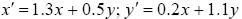

Рівняння (A.5),(A.6) визначають загальну форму запису афінного перетворення рис.А.2). До будь-якого афінного перетворення існує зворотнє, яке також є афінним. Добуток прямого і зворотнього перетворень дає одиничне перетворення, яке залишає все на місці.

В афінних перетвореннях площини особливу роль відіграють декілька важливих часткових випадків, які мають простий і наглядний геометричний зміст.

1.Розтягування (зтискання) вздовж координатних осей, задане у виді:

9

Розтягуванню вздовж відповідної осі відповідає значення масштабного множника, більшого за одиницю.

2.Поворот довкола початкової точки на кут , описується формулою:

3.Перенос, який задається простими співвідношеннями:

4.Відображення (відносно якоїсь з осей, наприклад осі абсцис) задається з допомогою формули:

Будь-яке афінне перетворення (A.5) завжди можна представити у виді композиції послідовно виконуваних простіших перетворень означеного виду. Афінні перетворення утворюють афінну групу. Зокрема, підгрупою афінної групи перетворень є група подібності (містить перетворення зсуву, повороту і зміни масштабу):

Знаючи параметри афінного перетворення, можна розрахувати безпосередньо і параметри оберненого перетворення

розв’язавши систему рівнянь (5.5) відносно (x, y) :

Якщо параметри такі, що (1 a)(1 e) bd то дане афінне перетворення має нерухому точку (X 0 ,Y0 ) :

Зауважимо, що при x Ax, c 0 початок координат і буде цією нерухомою точкою.

10