Добавил:

Justeeeek100500 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный университет Львовская политехника

Предмет:

Вища геодезія

Файл:

mtg_theme 5.pdf

Скачиваний:

Добавлен:

28.06.2022

Размер:

420.31 Кб

Скачать

☆

<<< < Предыдущая 12 / 52 3 4 5 > Следующая >>>

A0 1.5704606433 10 7 ,

A2 2.5184637 10 3 ,

A4 3.7002 10 6 ,

A6 7.4 10 9 ,

а коефіцієнти рядів (5.20) будуть тоді функціями широти Bx .

Перейдемо до визначення коефіцієнтів в рядах (5.20). Підставимо в рівняння (5.7) часткові похідні рядів (5.20), де замість аргументу x будем брати аргумент X . Тоді отримаємо

d a 2

y 2

d a4

d a6

y6 ...

N cos B

(

1 3

3 y 2 5

5 y4

7 y 7 ...),

N cos B db

db3

db5

2a 2 y

4a4 y

6a6 y

...

... .

Із порівняння між собою в цих рівностях коефіцієнтів при однакових степенях y , знайдемо

N cos B dX

3N cos B dX

....

a 2 N cos B db1 , 2M dX

a4 N cos B db3 , 4 M dX

Для знаходження всіх необхідних коефіцієнтів застосовуємо послідовне диференціювання по довжині дуги меридіана X , враховуючи при цьому, що

dB	M 1 ,	df (B)	df (B)	dB	.
		dX
dX			dB dX

Остаточні значення коефіцієнтів рядів (5.20) мають наступний вигляд

			1
b1			1						,


				N x cos Bx
						1 tgBx				2		2
a 2						1 tgBx		(1 e'		2	cos	2	Bx ),

						2 N x 2								(5.21)
						2 N x 2								(5.21)
		3			1			1		(1 2tg 2 Bx				e'2 cos2 Bx ),
	b				1			1
	b				6 N x		3 cos Bx
					6 N x		3 cos Bx

126

			1					tgBx							2				2			2					2		2		2			4		4				2		4		4
a 4			1					tgBx			(5 3tg				2	Bx 6e'			2	cos		2	Bx 6tg				2	Bx e'	2	cos	2	Bx	3e'	4	cos	4	Bx	9tg		2	Bx e'	4	cos	4	Bx ),

					24 N x				4
					24 N x				4
		5		1							1			(5 28tg 2 Bx							24tg 4 Bx					6e'2 cos2					Bx		8tg 2 Bx e'2 cos2						Bx ),
	b			1							1
	b
			120 N x							5 cos Bx
							1 tgBx										2							4
a6							1 tgBx						(61 90tg				2	Bx	45tg					4	Bx ).

						720 N x						6
						720 N x						6

Обчислені таким чином геодезичні координати будуть виражені в радіанній мірі. Точність цих формул така, що вони забезпечують 0.0001"в координатах B,l при розміщені точки на краю шестиградусної зони.

5.5.2. Формули для обчислення зближення меридіанів

Для визначення зближення меридіанів скористаємось другою формулою (5.4)

(5.22)

часткові похідні в якій знайдемо на основі формул (5.15). Отримаємо

2 l 4a4 l 3

6a6l5 ...,

(5.22’)

3b l 2 5b l 4 ....

Підставивши значення похідних у (5.22), отримаємо

l 4a

l 3 6a

(5.23)

b 3b l 2 5b l 4

Значення коефіцієнтів a2 , a4 , a6 ,b1 ,b3 ,b5

даються виразами (5.16), підставивши які в

(5.23) і виконавши елементарні математичні перетворення, остаточно отримаємо

tg sin Bl

sin B

1 tg 2 B 3e'2 cos2 B l 3

sin B

2 4tg 2 B 2tg 4 B l 5 .

(5.24)

3 cos2

15 cos4 B

Аналогічним чином можна знайти вираз для обчислення зближення меридіанів за плоскими прямокутними координатами, тільки при цьому за вихідну беруть другу формулу

(5.8)

B		L
tg M		: N cos B		.

	y		y

Приведемо остаточну формулу для зближення меридіанів у функції плоских прямокутних координат

127

tg		tgBx			y	tgBx		(1 tg 2 Bx e'2 cos2	Bx )y3

			N x			3N x	3		(5.25)
	tgBx
				(2 5tg 2 Bx				3tg4 Bx 2e'2 cos2	Bx tg 2 Bx e'2 cos2 Bx )y5 .
	15N x		5

У формулах (5.24) і (5.25) не враховано члени з e'4 . Точність приведених формул забезпечує обчислення в 0.001".

Знак зближення меридіанів співпадає зі знаком різниці довгот l або знаком y , тобто для точок, які розташовані на схід від осьового меридіану, зближення меридіанів завжди буде додатнім, а на захід від нього - від’ємним.

5.5.3. Формули для обчислення масштабу проекції

Для знаходження формули масштабу зображення скористаємось формулою (5.5), яку представимо у вигляді

	2	x	2	y	2			1
m	2	x		y				1			.	(5.26)


		L		L		N	2	cos	2	B
		L		L		N		cos		B

Вирази для часткових похідних нами вже отримано - ф-ли (5.22’). Підставивши квадрати цих виразів у (5.26) і додавши їх, отримаємо

m2	b 2	(4a	2	6b b	)l 2 (16a	2	a	4	9b	3	2 5b b )l 4
	1		2	1 3		2		4		3	1 5	.
					N 2 cos2 B							.
					N 2 cos2 B

В цій формулі збережено члени порядку l 4 . З врахуванням виразів для a					2	, a	4	,b ,b ,b (без
					2		4	1	3	5
сфероїдних членів при l 4 ) та простих алгебраїчних перетворень остаточно знаходимо
m 1	1	cos2 B(1 e'2 cos2 B)l 2	1	cos4 B(5 4tg 2 B)l 4 .						(5.27)
m 1		cos2 B(1 e'2 cos2 B)l 2	24	cos4 B(5 4tg 2 B)l 4 .						(5.27)
2			24

Як видно із даної формули, при l 0 , тобто на осьовому меридіані, масштаб проекції рівний одиниці. При віддалені від осьового меридіана на схід і на захід значення масштабу швидко зростає.

Для отримання формули масштабу зображення у функції плоских прямокутних координат скористаємось другою формулою (5.19), яку, з прийнятими вище обмеженнями, запишемо

	1		3		3		2
y Nl cos B		Nl		cos		B(1 tg		B).
y Nl cos B	6	Nl		cos		B(1 tg		B).
	6

Застосовуючи формули обертання ряду для l cos B , знайдемо

l cos B	y	(1 tg	2	B)	y3	,
	N				6N 3

128

звідки з прийнятою точністю

cos

(1 tg

N 2

3N 4

l 4

cos4

N 4

З врахуванням останніх двох виразів формулу (5.27) можна записати у наступному вигляді

			1		(1 e' 2 cos2					Bx )			2		1 ( 5 4tg 2 Bx		)		4
	m 1										y							y		.	(5.28)
	m 1							N x			y					N x 4		y		.	(5.28)
			2					N x	2					24		N x 4
	Оскільки
1 e' 2 cos 2 Bx				1			,
	N x						,
	N x	2				R 2
де R - середній радіус кривини еліпсоїда, то остаточно отримаємо
			m	1				y 2		y4		.									(5.29)
			m	1				2R 2		24R4		.									(5.29)
								2R 2		24R4
	В останньому члені формули (5.29) замість																N 4 приведено				R4 , що викличе похибку

порядку e4 на сфероїдні члени, якими знехтувано у членах порядку l 4 .

Масштаб зображення є дуже важливою характеристикою конформної проекції. Згідно формули (5.28) або (5.29) можна встановити величини і розподіл лінійних спотворень при

переході з еліпсоїда на площину. Так легко замітити, що із збільшенням ординати			y лінійні
спотворення зростають пропорційно y 2 ;		постійному значенню ординати	y const
відповідає практично постійна величина масштабу m const . Величина радіуса

R	a	1 e2
R
1 e2 sin 2 B

із зміною широти змінюється звісно, але досить незначно. Тому лінії рівних спотворень довжин в проекції Гаусса-Крюгера розташовуються практично паралельно осі абсцис на всій смузі проекції від екватора до полюса, а звідси виходить, що проекцію Гаусса-Крюгера найбільш оптимально застосовувати для зображення смуги, яка витягнута на еліпсоїді з півдня на північ. Межами такої смуги служать лінії рівних спотворень довжин m const .

129

5.5.4. Формули для редукування напрямів і відстаней

Під редукуванням напрямів і відстаней розуміють перехід від напрямів і довжин геодезичних ліній на еліпсоїді до відповідних їм величин на площині. Редукція напрямів полягає у визначенні поправки за кривину зображення геодезичної лінії на площині, а редукція відстаней - знаходженні різниці довжини геодезичної лінії та хорди зображення геодезичної лінії. Після введення цих редукцій у виміряні величини, які приведені на поверхню еліпсоїда, ми отримаємо геодезичну мережу, редуковану з еліпсоїда на площину.

На практиці редукування мережі 1–го класу на площину проводиться тільки в окремих випадках і не має широкого розповсюдження, тому при виводі формул будемо орієнтуватися на мережі нижчих (2-4) класів.

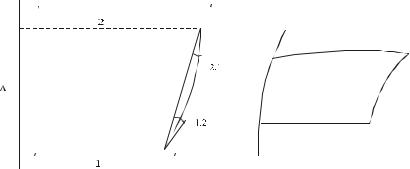
Для редукування напрямів вважатимемо, що AB є геодезичною лінією на поверхні еліпсоїда в складі деякої замкнутої геодезичної фігури ABDC (рис. 5.5.б).

		D		y	B
	x					D	B


					a
						C	A
						C	A
		C		y	A

				а)	Рис.5.5		б)
					Рис.5.5
Нехай геодезична лінія AB зображена на площині в виді кривої A' aB' (рис. 5.5.а). Кути
в точках A' і B'		між дотичними до кривої і хордою					A' B' позначимо через	12 і 21 .
Координати точок		A'	і B' позначимо через x1 , y1			і x2 , y2 . Нехай точки C' і D'		є основами
ординат точок A'		і	B'	відповідно.	Із-за конформності проекції фігури ABCD і A’B’C’D’

будуть подібними, а відповідні кути у них рівними. Суми внутрішніх кутів складуть:

на еліпсоїді A B C D 360o ;

на площині A' B' C' D' 360o ( 12 21 ) .

Значить, 12 21 , тобто сферичний надлишок рівний сумі поправок взаємообернених напрямів. Як відомо (див. розділ 3), сферичний надлишок визначається формулою

							P	,
							R 2	,
							R 2
де P - площа фігури A’B’C’D’; P				y1 y2	(x	2	x1 ) ym x .
де P - площа фігури A’B’C’D’; P					(x	2	x1 ) ym x .
Тоді			2
Тоді
12	21	ym	x.
12	21	R2	x.
		R2

Приймаючи наближено, 12 21 , отримуємо

130

x	ym	.	(5.30)

	2R 2

На практиці потрібно знати не тільки величину кута для даного напряму, але і як ввести його в цей напрям, щоб перейти на площині від кривих ліній до їхніх хорд. Оскільки відрахування кутів ведеться за ходом годинникової стрілки, то із рис. 5.5.а) легко видно, що для переходу від напряму A' aB' до хорди A' B' кут при точці A' потрібно відняти від напряму A' aB' , а при точці B' - додати до напряму B' aA'. Отже, поправки 12 і 21 у взаємні напрями мають протилежні знаки:


	"	"		(x			x )y		m	,
12	"			(x		2	x )y			,
12		2R2				2		1
		2R2										(5.31)
			"									(5.31)
	"		"		(x			x )y			m	.
21	"				(x		2	x )y				.
21			2R2				2	1
			2R2

Формулами (5.31) користуються для редукування напрямів в тріангуляції 3 класу і

нижче.

Поправки за редукцію алгебраїчно віднімаються від виміряних напрямів.

Значення редукованих плоских кутів A’,B’ і C’ за виміряними на фізичній поверхні і приведеними на еліпсоїд кутами A,B і C трикутника ABC отримують наступним чином

A' A ( AC AB ) A A ;

B' B ( BA BC ) B B ;

C' C ( CB CA ) C C .

Сума поправок за редукцію кутів трикутника рівна його сферичному надлишку з оберненим знаком, що служить контролем обчислення та . Справді,

A' B' C' A B C ( A B C ),

A B C A' B' C' ,

( A B C ) .

В тріангуляції 2-го класу для обчислення поправок за кривину зображення геодезичних ліній застосовують більш точні формули, які приведемо без доведення

			x		( 2y		y		);
	12							2
		6Rm 2			1
									(5.32)
				x
21						( 2y2 y1 ),
				6Rm	2

де Rm - середній радіус кривини, обчислений за широтою середньої точки заданої

геодезичної лінії.

Як видно з наведених формул, для обчислення редукцій повинні бути відомі плоскі прямокутні координати початкового і кінцевого пунктів. Визначимо необхідну точність цих

131

<<< < Предыдущая 12 / 52 3 4 5 > Следующая >>>

Соседние файлы в предмете Вища геодезія

#
28.06.2022829.03 Кб3journal-lab-p1.pdf
#
28.06.2022459.29 Кб2mtg_theme 1.pdf
#
28.06.2022325.88 Кб1mtg_theme 2.pdf
#
28.06.2022251.9 Кб3mtg_theme 3.pdf
#
28.06.2022539.81 Кб6mtg_theme 4.pdf
#
28.06.2022420.31 Кб1mtg_theme 5.pdf
#
28.06.2022372.82 Кб1mtg_theme 6.pdf
#
28.06.2022240.33 Кб1mtg_theme 7.pdf
#
28.06.2022164.8 Кб1mtg_theme 8.pdf
#
28.06.2022206.31 Кб3mtg_theme 9.pdf
#
28.06.202223.3 Mб9Закатов Вища геодезія 1.pdf