
mtg_theme 3
.pdf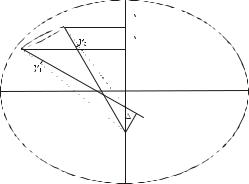
Тема 3. Криві на поверхні еліпсоїда
РОЗДІЛ 3
КРИВІ НА ПОВЕРХНІ ЕЛІПСОЇДА
3.1. Нормальні перерізи на поверхні еліпсоїда
Із множини кривих, які можна провести через дану точку поверхні еліпсоїда, особливу зацікавленість представляють плоскі перерізи, які утворюються від перетину поверхні еліпсоїда площиною, що проходить через нормаль до даної поверхні.
Слід відзначити, що в загальному випадку плоский переріз еліпсоїда є еліпс. Якщо нормальний переріз перпендикулярний площині екватора, то він перетворюються в меридіанний еліпс, а нормальний переріз в заданій точці, що проходить під азимутом 90° є першим вертикалом цієї точки. Перерізи, утворені площинами,
паралельними площині екватора, будуть колами і називаються паралелями, а перерізи, які утворені площинами,
що проходять через центр еліпсоїда називаються центральними перерізами.
В сфероїдній геодезії нормальні перерізи знаходять широке застосування, тому розглянемо їх детальніше.
Особливістю нормального перерізу є наявність у нього хоча б однієї геодезичної точки - точки, в якій головна нормаль кривої збігається з нормаллю до поверхні еліпсоїда. Через задану точку на поверхні можна провести скільки завгодно нормальних перерізів.
Якщо на поверхні еліпсоїда візьмемо дві точки А і В з широтами В1, та В2 відповідно (рис.3.1), при цьому
B2 B1 , то нормаль до поверхні еліпсоїда, проведена в точці A перетинає малу вісь ближче до центру еліпсоїда ніж нормаль в точці B,
|
|
P |
|
|
B |
B |
|
A |
b |
A |
|
a |
|
||
E 1 |
|
O |
E |
|
n1 n |
||
|
|
|
|
|
|
n2 |
|
|
|
P1 |
|
тобто On1 On2 (а).
Ці нормалі - це дві перехресні в просторі прямі, що не перетинаються (якщо точки A і B не лежать на одному меридіані).
Рис. 3.1. Взаємооберенені нормальні перерізи
Докажемо, що нормальні перерізи між двома точками на еліпсоїді в загальному випадку не збігаються.
Із трикутника AA' n1 (рис.3.1) маємо
n1 A' N1 cos(900 B1 ) N1 sin B1 ,
On1 n1 A' A'O.
або
On N |
1 |
sin B N |
1 |
(1 e2 )sin B |
e2 N |
1 |
sin B . |
(3.1) |
|||
1 |
|
|
1 |
|
1 |
|
1 |
|
|||
Із трикутника BB' n2 (рис.3.1) маємо |
|
|
|
|
|
|
|
|
|
|
|
n2 B' N 2 cos(900 |
B2 ) N 2 sin B2 , |
|
|
|
|||||||
|
|
On2 n2 B' B'O, |
|
|
|
|
|
||||
або |
|
|
|
|
|
|
|
|
|
|
|
On2 N2 |
sin B2 |
N2 (1 e2 )sin B2 |
e2 N2 sin B2 . |
(3.2) |
|||||||

Тема 3. Криві на поверхні еліпсоїда
Отже, при B2 B1 буде виконуватися умова (а); нормальні перерізи (криві АаВ і ВbА) при цьому розташуються так, як показано на рис 3.1, тобто крива ВbА північніше кривої АаВ.
Візьмемо площину, що включає нормаль Аn1 і проходить через точку В. Очевидно, що ця площина є нормальною площиною в точці А, що проходить через точку В. На поверхні еліпсоїда ця площина утворює криву АаВ, що називається прямим нормальним перерізом в точці А на точку В і оберненим нормальним перерізом в точці В на точку А.
Інша площина, що включає нормаль в точці B і проходить через точку А, утворює на поверхні еліпсоїда криву ВbА – прямий нормальний переріз з точки B на точку A , що не збігається з кривою АаВ.
Ці дві криві АаВ і ВbА називаються взаємними нормальними перерізами.
Так, між двома точками еліпсоїда A і В в загальному випадку проходять два нормальних перерізи:
АаВ - називається прямим нормальним перерізом для точки А і оберненим нормальним перерізом для точки В;
ВbА - називається прямим нормальним перерізом для точки В і оберненим нормальним перерізом для точки А.
Знайдемо кут 1 , під яким видно відрізок n1n2 із точки А (див. рис.3.1). Із прямокутного трикутника
nn1n2 , в якому n1n2 є гіпотенузою, знайдемо
nn1 n1n2 sin B1 , |
nn2 n1n2 cos B1. |
|
|||
Тоді кут 1 можна визначити із прямокутного трикутника Ann2 : |
|
||||
tg 1 |
n1n2 |
cos B1 |
. |
(3.3) |
|
N1 n1n2 sin B1 |
|||||
|
|
|
|||
Аналогічним чином можна знайти і кут 2
tg 2 |
|
n1n2 |
cos B2 |
. |
(3.4) |
||
N2 |
n1n2 sin B2 |
||||||
|
|
|
|
||||
З формул (3.1) та (3.2) для відрізка n1n2 отримаємо
n n |
2 |
e2 (N |
2 |
sin B |
2 |
N |
1 |
sin B ) |
(3.5) |
1 |
|
|
|
1 |
|
Вираз для кута між взаємними нормальними перерізами ВbА і АаВ виводиться у чисельних класичних
s
підручниках з вищої геодезії. З точністю до малих величин третього порядку e2 3 , де N m , запишемо
|
1 |
e2 2 cos2 Bm sin 2A. |
(3.6) |
|
4 |
||||
|
|
|
Із формули (3.6) слідує, що величина А переходить в нуль двічі: при А =0 і при А = 90 . Іншими словами,
взаємні нормальні перерізи збігаються, якщо пункти лежать на одному меридіані або на одній паралелі. Цей висновок справедливий лише з тією точністю, з якою виведена формула (3.6).
Крім кута між взаємними нормальними перерізами, розглянемо також лінійну розбіжність між ними, яка,
очевидно, буде максимальною для середніх точок дуг АаВ та ВbА (рис. 3.2).
Формула для обчислення найбільшої лінійної розбіжності між перерізами АаВ і ВbА буде наступною

Тема 3. Криві на поверхні еліпсоїда
q |
|
1 |
N |
|
e2 |
|
|
B |
|
sin 2A |
|
|
max |
|
|
m |
3 |
cos2 |
m |
(3.7) |
|||||
|
||||||||||||
|
16 |
|
|
|
|
|
|
|
||||
|
P |
|
b |
B |
|
|
||
|
a |
|
q |
||
|
|
Рис. 3.2. До питання про лінійне розходження |
Nm |
взаємних нормальних перерізів. |
A |
|
n1
n2
Таблиця 3.1 дає представлення про числові значення величин та q.
Таблиця 3.1. Кутові та лінійні розходження між взаємними нормальними перерізами
A , |
B , |
s,км |
" |
q, мм |
45 |
50 |
30 |
0.003 |
0.1 |
|
|
|
|
|
45 |
50 |
100 |
0.031 |
3.7 |
|
|
|
|
|
45 |
50 |
150 |
0.056 |
12.8 |
|
|
|
|
|
Значення та q показують, що для типових довжин сторін класичних геодезичних мереж, які створювались переважно методом тріангуляції, в 20-25 км подвійним характером нормальних перерізів можна не рахуватися. При опрацюванні першокласних тріангуляцій остаточні значення азимутів виводяться із сотими долями секунди, тобто похибки окремих обчислювальних процедур, при передачі азимута не повинні перевищувати ± 0.002-0.003". Тому очевидно, що при високоточній передачі азимутів, коли сторони можуть перевищувати 30км приходиться рахуватися із кутовою різницею між взаємними нормальними перерізами.
Уявімо собі, що в точці A встановлений кутомірний прилад таким чином, що його вертикальна вісь збігається з нормаллю Ana (рис.3.3); тоді при наведені на точку B площина візування збігається з площиною,
що проходить через точки A, na , B , або, як вище було зазначено, з площиною прямого нормального перерізу із точки А на точку В. Перетином цієї площини з поверхнею еліпсоїда буде крива AaB .
P
a B
A |
a C |
|
 na
na
При аналогічному наведені на точку C
площина перетне поверхню еліпсоїда по деякій кривій яка буде прямим нормальним перерізом із точки А на точку
С. Горизонтальний кут в точці А між напрямами на точки В і С буде мірою двогранного кута BAna C між нормальними площинами в А, що проходять через точки В і С .
Рис. 3.3. Горизонтальні кути на поверхні еліпсоїда.
Тема 3. Криві на поверхні еліпсоїда
Отже, вимірювані в тріангуляції горизонтальні кути на поверхні еліпсоїда є кутами між прямими нормальними перерізами в даній точці.
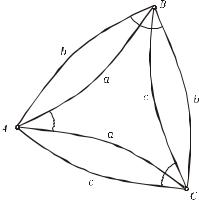
Якщо взяти трикутник, у вершинах якого виміряні кути, то внаслідок неспівпадання прямих і обернених нормальних перерізів, отримана із вимірювань фігура буде мати шість сторін (рис.3.4).
Очевидно, що неспівпадання прямих і обернених нормальних перерізів приводить до того, що на поверхні еліпсоїда виміряні горизонтальні кути не утворюють замкнутого трикутника (виміряні кути на кожному пункті показані дугою).
Рис. 3.4. Розходження взаємних нормальних перерізів у трикутнику
Щоб не мати справи з подвійним характером нормальних перерізів, геометричні фігури на поверхні еліпсоїда можна утворювати або хордами нормальних перерізів, або геодезичними лініями.
Застосування хорд еліпсоїда хоча і в деяких часткових випадках приводить до виразів в замкнутій формі
(замість нескінченних рядів), проте хорда не володіє таким узагальненням як геодезична лінія для розв'язування задач сфероїдної геодезії.
Отже, подвійний характер нормальних перерізів послужив однією із головних причин для утворення фігур на поверхні еліпсоїда із геодезичних ліній.
3.2. Геодезичиа лінія
Геодезичні лінії мають велике значення в сфероїдній геодезії. Якщо на площині розв'язування геодезичних задач проводиться з відрізками прямих та прямолінійними фігурами, а на сфері задачі розв'язуються з лініями великих кіл, то на еліпсоїді мають справу з геодезичними лініями та фігурами, що ними утворені.
Теорія геодезичних ліній розвинулась в зв'язку з широким застосуванням градусних вимірювань, значну роль в яких грали геодезичні трикутники. Дослідження, проведені з цього питання Клеро, Лежандром, Гауссом та іншими вченими, виявили властивості геодезичних ліній на різних поверхнях, в тому числі і на поверхні еліпсоїда обертання. Геодезична лінія на поверхні в межах деякої обмеженої області володіє наступними властивостями, аналогічними властивостям відрізку прямої на площині:
Геодезична лінія є найкоротшою відстанню між двома точками.
Через дві точки поверхні можна провести тільки одну геодезичну лінію.
Через задану точку поверхні в заданому напрямі проходить тільки одна геодезична лінія.
На гладкій поверхні матеріальна точка рухається за інерцією вздовж геодезичної лінії; натягнута на такій поверхні нитка розташовується по дузі геодезичної лінії.
Авзагалі, якщо стична площина в будь-якій точці лінії буде нормальна до поверхні, то така лінія і буде для даної поверхні геодезичною.
Площину, що вміщує дотичну до кривої в даній точці і точку на кривій, нескінченно близьку до точки
дотику, називають стичною площиною (див. рис.1.8).

Тема 3. Криві на поверхні еліпсоїда
Геодезичну лінію на поверхні еліпсоїда можна побудувати наступним способом. Сумістивши в даній точці А (див. рис.3.5) вертикальну вісь кутомірного приладу з нормаллю до поверхні еліпсоїда, з допомогою візирної труби відмічають на цій поверхні в заданому напрямі точку a1 . Перемістивши прилад в точку а1 та сумістивши його вертикальну вісь з нормаллю до поверхні еліпсоїда в цій точці, направляють візирну вісь на попередню точку А. Після цього, повернувши трубу на 180 відмічають наступну точку a2. Потім переносять прилад в точку a2, візують на точку а1 і відмічають на 180 від неї положення точки а3. Послідовно переходячи в точки а3, a4 і т.д., відмічають точки а4, a5… Зменшуючи відстані між суміжними точками (в границі до нескінченно малої величини), отримаємо лінію, яка і буде геодезичною лінією заданого напряму.
Дійсно, площина, що проходить через будь-які три суміжні точки аi-l, ai, ai+l буде стичною площиною, яка проходить через нормаль еліпсоїда в точці аi тобто будь-яка точка, що побудована таким чином буде геодезичною.
В розглянутому методі побудови геодезичної лінії кожна наступна точка визначається двома їй попередніми при умові прямування до нуля відстані між кожними двома суміжними точками.
Рис. 3.5. Геометрична побудова геодезичної лінії (1 спосіб)
Існує інший спосіб побудови геодезичної лінії між точками А і В. Нехай AaB - прямий нормальний переріз в точці А, а BbA - в точці В (див. рис. 3.6). З’єднаємо точки А і В хордою; проведемо нормаль із середини даної хорди до поверхні еліпсоїда і позначимо точку перетину цієї нормалі з поверхнею еліпсоїда через С.
B
|
b |
|
b |
J |
|
|
bH |
E |
|
|
|
c |
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
C |
|
|
c |
G |
a |
|
|
|
|
|
F  D a d
D a d a
a
A
Рис. 3.6. Геометрична побудова геодезичної лінії (2 спосіб)

Тема 3. Криві на поверхні еліпсоїда
Через точку А та нормаль в точці С проведемо площину. Поскільки в цій площині буде лежати хорда АВ,
то площина пройде через В. На рис. 3.6 переріз цією площиною поверхні еліпсоїда показано кривою AcCcB .
Очевидно, ця площина буде площиною прямого нормального перерізу із точки С на точки А і В. Оскільки точка
С розташована на північ від А, то прямий нормальний переріз в А, що з’єднує цю точку з С , зобразиться
кривою AaC , яка буде розташовуватись на поверхні еліпсоїда південіше, ніж обернений переріз CcA .
Аналогічно, оскільки точка В розташована на північ від С, то прямий нормальний переріз в В, що з’єднує точки
В і С, зобразиться кривою BbC , яка буде розташована північніше нормального перерізу CcB . З’єднавши хордами точки А і С та С і В, знайдемо на цих хордах середні точки і в них проведемо нормалі до поверхні еліпсоїда (нехай перетини цих нормалей з поверхнею еліпсоїда будуть відповідно в D і E).
Проведемо нормальну площину в D через А і в той же час через точку С. На поверхні еліпсоїда отримаємо криву AdDdC , що буде мати нормаль в точці D. Аналогічно отримаємо криву CcEeB , що має нормаль в точці E. Очевидно, прямий нормальний переріз в А, що з’єднує цю точку з D, зобразиться кривою
AaD ; прямий нормальний переріз в С, що з’єднує цю точку з D, зобразиться кривою CcD ; прямий нормальний переріз в В, що з’єднує цю точку з Е, зобразиться кривою BbE , а прямий нормальний переріз в С,
що з’єднує цю точку з Е, зобразиться кривою CcE . З’єднавши послідовно хордами А і D, D і С, C і E, E і B,
проводимо нормалі до поверхні еліпсоїда в серединах цих хорд і відмічаємо точки F, G, H, J перетину цих нормалей з поверхнею еліпсоїда. Подальші дії аналогічні вище наведеному.
Якщо представити собі продовження цього процесу до нескінченності, то в границі нього ми прийдемо до елементарних хорд, кінці яких дадуть на поверхні еліпсоїда неперервну криву, що розташована між точками
А і В . При цьому площина, що проходить через нормаль до еліпсоїда, яка проведена із середини деякої елементарної хорди і через саму хорду, перетвориться в стичну площину отриманої кривої в точці, що відповідає середині даної хорди. Тому побудовані точки утворять неперервну криву AFDGCHEJB , яка і буде геодезичною лінією між А і В , оскільки виконана умова, що визначає геодезичну лінію: в кожній точці її нормаль до поверхні буде лежати в стичній площині кривої.
З достатньою точністю можна прийняти, що при азимутах, не близьких до 90 або 2700 , нормальний переріз, що проходить через нормаль до поверхні еліпсоїда, яка проведена із середини хорди А і В, ділить кути між взаємними нормальними перерізами навпіл. Оскільки переріз AcCcB (рис. 3.6) ділить навпіл кути при А і В між кривими AaB і BbA , переріз AdDdC ділить навпіл кути при А і С між кривими AaC і AcC , то скористаємось вказаною властивістю кривих на поверхні еліпсоїда для виводу кута між геодезичною лінією і прямим нормальним перерізом. Якщо - кут між взаємними нормальними перерізами в точці А, тобто між кривими AaB і BbA , то - кут першого елемента геодезичної лінії в А з прямим нормальним перерізом на В,
тобто з кривою AaB (рис. 3.7).
B
b
Рис. 3.7. Кути між нормальними перерізами та геодезичною лінією.
a
A
Будемо мати такі кути між кривими:

Тема 3. Криві на поверхні еліпсоїда
AcC |
i |
AaB |
|
|
|
|
|
||||||||||||
|
|
|
|
|
, |
|
|||||||||||||
2 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
AcC |
|
|
AaC |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
, |
|
|||||||||||
|
|
4 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
AdD |
|
i |
AaC |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
, |
|
|||||||||||||
|
8 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
AdD |
i |
AaB ..................... |
|
|
|
|
|
|
|
|
, |
||||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
2 |
|
8 |
|
|||||||||||||
AdD |
|
i |
AaD |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
, |
|
|||||||||||||
|
16 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
AdD |
|
i |
AfD |
|
|
|
|
|
|
||||||||||
|
|
|
|
, |
|
||||||||||||||
|
|
32 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
AfD i |
AaB |
|
|
|
|
|
|
||||||||||||
..................... |
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
8 |
|
|
32 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
тощо.
По аналогії з вище наведеним процесом утворення кутів між кривими, в границі кут між кривою AaB та першим елементом геодезичної лінії в А буде:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
..., |
||||||||||
|
|
|
8 |
32 |
128 |
512 |
|||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
1 |
|
|
1 |
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... . |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
2 |
4 |
|
|
16 |
|
|
|
|
64 |
|
|
|
256 |
|
|
||||||||||||||||||||||
Або |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
1 |
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... . |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
2 |
|
|
4 |
16 |
|
|
|
|
64 |
|
|
|
256 |
|
|
||||||||||||||||||||||||
Сума членів геометричної прогресії, що стоїть в круглих дужках, буде |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Відповідно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
3 |
|
|
|
|
|
|
|
||||||||||||||||
або, з врахуванням (3.6) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
e2 2 cos2 |
Bm sin 2A, |
(3.8) |
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Отже, кут між геодезичною лінією, що з’єднує точки А і В, та прямим нормальним перерізом в кожній з |
|||||||||||||||||||||||||||||||||||||||
1
цих точок дорівнює кута між прямим і оберненим нормальними перерізами в даній точці.
3
Розташування геодезичної лінії відносно взаємних нормальних перерізів в загальному випадку показано на рис.3.7; пунктирними лініями позначені продовження дуг нормальних перерізів.
В цілому геодезична лінія на всьому своєму проміжку між заданими пунктами завжди ближче розташовується до прямого нормального перерізу. Якщо азимути геодезичної лінії близькі до 0 і 90°,
розташування геодезичної лінії у відношенні нормальних перерізів дещо інше. Розглянемо окремо ці два випадки розташування геодезичної лінії відносно взаємних нормальних перерізів:

Тема 3. Криві на поверхні еліпсоїда
якщо азимут A12 0 або 1800 , то тоді кут буде рівний нулю (3.8), тобто прямий і обернений перерізи та геодезична лінія між двома точками, що знаходяться на одному меридіані, збігаються;
якщо дві точки знаходяться на одній паралелі, то геодезична лінія в цьому випадку або проходить поза фігурою, утвореною нормальними перерізами, або ж перетинає ці перерізи. Проте в цих випадках кут ,
що складає геодезична лінія з нормальними перерізами досить малий і тому ним нехтують.
Диференційне рівняння геодезичної лінії є рівнянням Ейлера для варіаційної проблеми найкоротшої відстані між двома точками на довільній поверхні і було виведене ним на основі законів механіки. Вивід рівняння геодезичної лінії із геометричного її визначення належить Лагранжу. Подальші дослідження цього
питання проведені Гауссом та Бесселем.
Детальний вивід диференційного рівняння геодезичної лінії можна знайти в літературі. Кінцевий вигляд цього рівняння наступний
dA |
sin A |
|
||
|
|
|
sin B. |
(3.9) |
|
|
|||
ds |
N cosB |
|
||
Рівняння (3.9) має важливе значення для дослідження геодезичної лінії, а разом з рівняннями (2.47) та
(2.48) є вихідним для розв'язування прямої та оберненої геодезичних задач на поверхні еліпсоїда. Із рівнянь
(3.9) та (2.47) знайдемо
|
dA |
M sin B |
||
|
|
|
|
tgA. |
|
|
|
||
|
dB |
N cos B |
||
Приймаючи до уваги, що |
|
|
||
|
|
|
r N cosB a cosu, |
|
|
|
|
|
|||||
|
|
|
cosu |
|
|
|
cosB |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 e2 sin2 B |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
отримаємо |
|
|
|
|
|
|
|
|
|
|
|
||
|
dA |
a sin udu |
|
d (a cosu) |
|
|
dr |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
tgA |
a cosu |
a cosu |
|
r |
|
|||||||
Після інтегрування |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
ln sin A ln r ln c . |
|
|||||||||
Або |
|
|
|
|
|
|
|
|
|
|
|
||
r sin A a cosu sin A N cosB sin A c const |
(3.10) |
||||||||||||
де с- постійна інтегрування. Рівняння (2.83) називають рівнянням Клеро. Із цього рівняння слідує, що на поверхні еліпсоїда добуток радіуса паралелі на синус азимута геодезичної лінії постійний для всіх точок геодезичної лінії. Постійну с можна знайти за широтою u , та азимутом А, в початковій точці геодезичної лінії,
тобто
c cosu1 sin A1 . |
(3.11) |
3.2.1. Різниці азимутів і довжин дуг геодезичної лінії та нормального перерізу
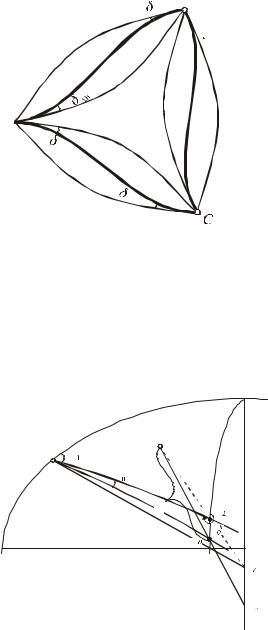
На рис. 3.4 зображено фігуру, утворену кутами між прямими нормальними перерізами. Якщо провести між вершинами геодезичні лінії, то отримаємо замкнутий трикутник, що утворений цими лініями, як показано на рис.3.8.
Для переходу до такої фігури достатньо в кожен напрям прямого нормального перерізу ввести поправкуза формулою (2.81), в результаті чого отримаємо кути трикутника, утвореного геодезичними лініями. Цю
Тема 3. Криві на поверхні еліпсоїда
поправку називають поправкою за різницю азимутів прямого нормального перерізу геодезичної лінії. Величина цієї поправки є незначною. Так при відстані між пунктами в 200км в найгіршому випадку (Ві =0 і А=45°)
величина складає 0.12", а при відстанях до З0км вона є меншою 0.001". Тому дана поправка, в звичайних за розмірах трикутниках тріангуляції, для одиночних передач азимутів, переважно, не вводиться. Але при послідовному обчисленні азимутів сторін тріангуляції по ланці неврахування цієї поправки може привести до систематичної похибки в азимуті сторони останнього трикутника ланки тріангуляції. Отже, поправку слід враховувати при математичному опрацюванні результатів кутових вимірювань в державних мережах 1 класу,
що створюються методом тріангуляції.
B
BA

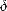 BC
BC
Рис. 3.8. Геометричне трактування поправки за перехід від прямих нормальних перерізів до геодезичних ліній.
A
AC
 CB
CB
CA
Двоїстість нормальних перерізів викликає необхідність також у виправленні виміряних напрямів поправкою за висоту пункту, що спостерігається. Приведемо геометричний зміст даної поправки.
Нехай на рис.3.9 A і B - два суміжних пункти тріангуляції. Якщо вертикальна вісь кутомірного приладу направлена вздовж нормалі до еліпсоїда, то висота пункту A над еліпсоїдом не вплине на величину вимірюваного кута.
|
|
P |
|
B |
|
A |
A |
|
|
d |
|
|
H |
A |
|
|
B |
|
|
B |
|
|
n |
|
|
n |
Рис. 3.9. Геометричне трактування поправки за висоту пункту спостереження.
Проте, напрям AB на точку B , яка розташована на висоті H 2 |
над еліпсоїдом, і напрям |
AB0 на |
||
проекцію цієї точки не співпадають. |
|
|
|
|
Напрям AB буде лежати в площині прямого нормального перерізу |
An B |
' , а напрям між проекціями |
||
|
|
1 |
0 |
|
точок A і B буде знаходитись в площині прямого нормального перерізу An1B0 . Поправку |
за висоту |
|||
пункту спостереження можна знайти із трикутника AB ' B |
, який вважатимемо плоским. Кути при вершинах |
|||
0 |
0 |
|
|
|
Тема 3. Криві на поверхні еліпсоїда
B0 і B0' цього трикутника можна прийняти за A2 1800 ( A2 - азимут оберненого напряму), а довжини AB0 і
AB ' - s , тоді |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
0 |
B |
' |
|
sin A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
|
|
|
|
|
|
|
0 |
|
|
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Відрізок B |
0 |
B |
' можна рахувати таким, що дорівнює дузі, яку стягує кут B |
' |
BB |
|
, тобто кут |
2 |
(див. рис. |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|||
3.1), а BB0 H 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Тоді, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
|
2 H 2 |
|
sin A . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Значення |
кута 2 підставимо із формули (3.4). При цьому врахуємо, що різниця широт для пунктів 1-го |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
класу не перевищує 20-30 |
(в радіанній мірі це буде |
|
|
|
1 |
|
), тобто величини |
n n |
2 |
, |
1 |
, |
2 |
- малі величини |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
120 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
другого порядку, тому в них можна N1 |
і N2 |
|
замінити через Nm - радіус кривини першого вертикала для точки |
||||||||||||||||||||||||||||||||||||||||||||||||||||
з середньою широтою Bm , а (sin B2 sin B1 ) B cos Bm . Тоді отримаємо |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
e2 B cos B |
m |
cos B |
2 |
|
|
|
e2 B cos |
2 B |
m |
|
e |
2 |
cos A cos2 B |
m |
. |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
(1 e2 B cos Bm sin |
|
B2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Оскільки |
|
|
2 -мала |
|
величина |
|
другого |
|
|
|
|
порядку, |
|
то |
|
можна |
|
прийняти |
|
|
sin A2 sin A1 , |
||||||||||||||||||||||||||||||||||
cos2 B |
m |
cos2 |
|
B |
|
. Тоді остаточно, поправка за висоту пункту спостереження, буде мати наступний вид |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
|
e2 |
|
H |
2 |
|
|
cos2 B sin 2A . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.12) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
a |
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
У формулі (3.12) |
H 2 |
|
є геодезична висота точки B , тобто висота, що відраховується не від рівня моря, а |
||||||||||||||||||||||||||||||||||||||||||||||||||||
від поверхні прийнятого еліпсоїда. При висоті H |
2 |
|
, що дорівнює 1000 м і при B 450 , |
|
A 450 |
, величина |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||
H складає 0.05" . Дана поправка вводиться у виміряні напрями тріангуляції 1-го класу, а деколи (особливо у |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
гірських районах) і тріангуляції 2-го класу. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Якщо поставити вимогу, щоб H |
0.001" , |
то з тими ж значеннями широти та азимута |
H 30 м, |
||||||||||||||||||||||||||||||||||||||||||||||||||||
тобто поправку H |
треба враховувати у першокласних геодезичних мережах вже при H 30 м. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
Знайдемо ще різницю довжин дуг геодезичної лінії s та нормального перерізу . Диференційна зміна |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
довжини дуги нормального перерізу буде визначатися на основі наступного співвідношення |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e4 s4 |
|
|
cos4 B sin2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
d ds |
1 |
|
|
|
|
|
|
|
|
|
2A |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
72N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Інтеграл цього диференціального рівняння буде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
e4 s5 |
|
cos4 B sin2 2A. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.13) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
360N 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
