Ряд Фурье с периодом .

Пусть определена на и удовлетворяет на отрезке . Разложим её в ряд Фурье. Положим и рассмотрим функцию . Разложим на в ряд Фурье: , где .

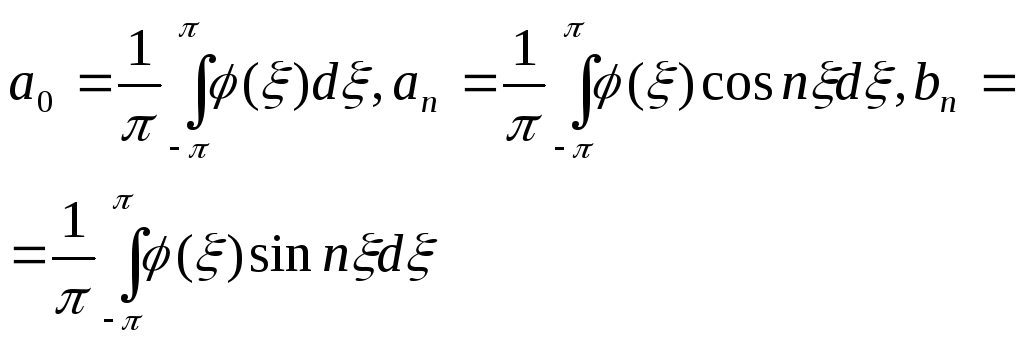П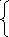ерейдем к примеру (4)примет вид:

,

.

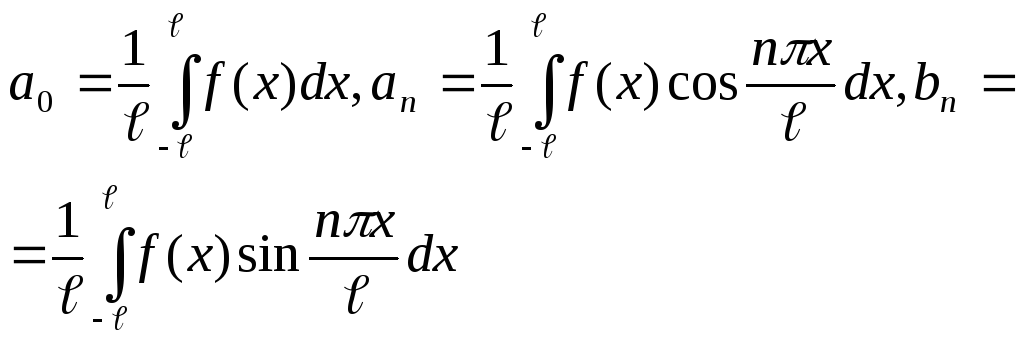№10. Линейные обыкновенные дифференциальные уравнения и их системы. Фундаментальная система решений. Определитель Вронского.

Опр1 Обыкновенным диф-ым уравн-м называется рав-во, содержащее независимую переменную х, независимую функцию у и ее производные у′,у′′,…,у⁽ⁿ⁾: F(x,y, у′,у′′,…,у⁽ⁿ⁾)=0 (1), F, если не оговорено предполагают действительной функцией.

Опр2. Диф-ое уравн-ие 1го порядка называется линейным, если его можно записать в виде у′+p(x)y=g(x),где p(x) и g(x) заданные функции, в частности постоянные. Линейным диф-м ур-м 2го порядка назыв-ся уравнение вида a(x) у′′+b(x) у′+c(x)y=f(x), где a(x)≠0,b(x),c(x),f(x)функции непрерывные на инт (а,b).Уравнение вида у⁽ⁿ⁾+a_n-1y^(n-1)+a₁y′+a₀y=0, где a_0, a_1,…, a_n-1=const(числа ≠0) назыв-ся линейным однородным уравнением n-го порядка.

Опр3 Пусть у₁=у₁(х),у₂=у₂(х) два каких-либо частных решения однородного диф-го уравн-я 2го порядка. Определитель вида W(x)=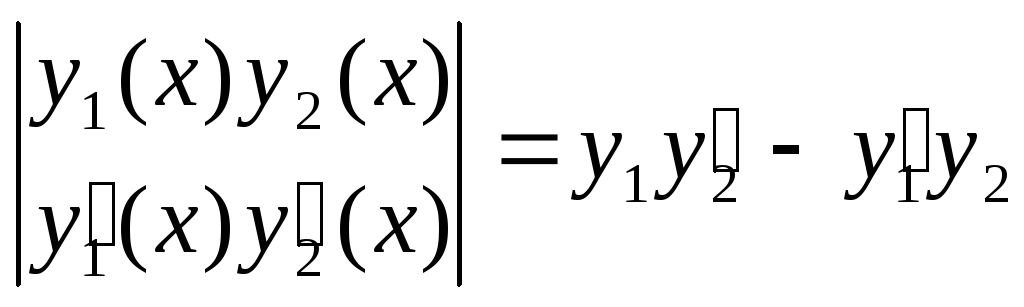 наз-ся определителем Вронского или вронскианом для у₁ и у_2.

Если опред-ль Вронского в точке х₀=0, то он =0 на всем интерв (a,b).Если опред Вронск в точке х₀≠0, то он ≠0 ни в одной точке инт-ла (a,b).

Опр4 Система частных решений у₁=у₁(х),у₂=у₂(х) однородного диф-го уравн-я 2го порядка наз-ся фундаментальной системой решения этого уравнения,если W(x) ≠0 на (a,b).

Опр5 Системой дифференциальных уравнений наз-ся система вида:

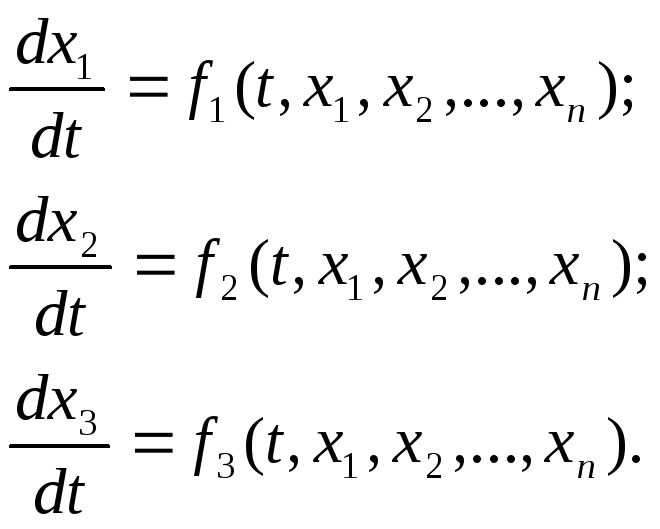
Опр6Система вида ==…=

наз-ся системой диф-ых ур-й в симметричной форме(?).

О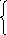пр7 Система диф-ых ур-й наз-ся линейной,если она линейна относительно неизвестных функций и их производных. Система n-линейных ур-ий 1го порядка, записанная в: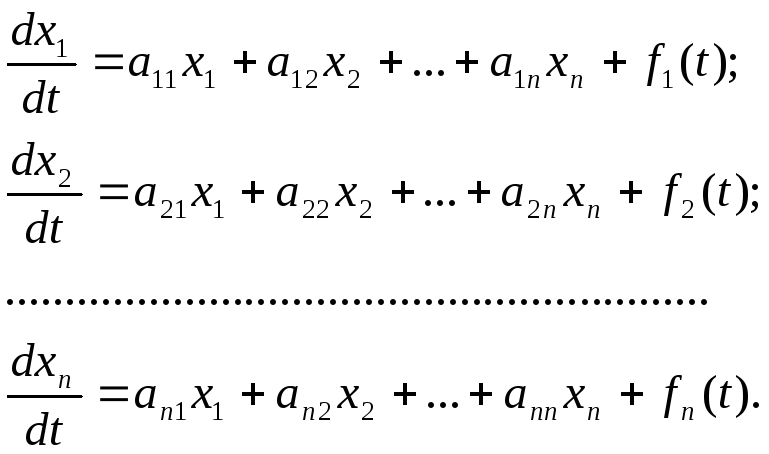или в матричной векторной форме

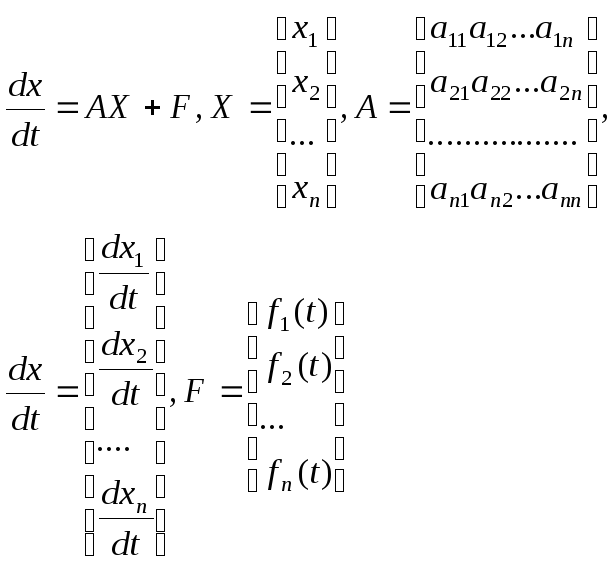
Опр8 Система n линейно независимых решений системы наз-ся ее фундаментальной системой решений,здесь A=A(t)-квадратная матрица разм. nn,элементы кот a_ij(t),ij=1,2,…,n непрерывные функции на I.

№11 Опр1 Интегр-м уравн-м наз-т ур-ие,которое сод-т некотор искомую функцию под знаком интегр.

Опр2 Ур-ие вида K(t,τ)y(τ)dτ+f(t), где y(t)-искомая функция,а f(t)- задан на интерв (a,b) функция наз-ся ур-ем Фредгольма 2го рода. Уравнение вида K(t,τ)y(τ)dτ=f(t) наз-ся ур-ем Фредгольма 1го рода, где K(t,τ)-ядро этих интегр-х уравнений, f(t)-свободный член.

Опр3 Ядро интегр-го ур-ия K(t,τ),которое можно представить в виде

K(t,τ)= наз-ся вырожденным ядром.

Уравнение Фредгольма с вырожденным ядром выглядит так: ,

λ-параметр.

12. Вероятностное пространство. Случайные величины. Закон больших чисел в форме Чебышева.

Опр. Набор трёх объектов , где -произвольное непустое множество, -алгебра подмножеств , - мера на и , наз. Вероятностным пространством.

Пусть дано вероятностное пространство и под случайной величиной понимаем некоторую функцию.

Опр. Числовая функция от элементарного события называется случайной величиной, если для любого числа x справедливо: .

Смысл определения: т.к. не любое подмножество является событием и все события составляют -алгебру подмножеств , то естественно рассмотреть такие , для которых имеет смысл говорить о вероятности попадания в достаточно простые числовые множества .

Известно, что нельзя заранее предвидеть, какие из возможных значений примет случайная величина в результате испытания, но при некоторых широких условиях суммарное поведение достаточно большого числа случ. Величин утрачивает случайный характер и становится закономерным. Эти условия указывают в теоремах под общим названием закон больших чисел.

Теорема ( нер-во Чебышева). Для любого >0 имеют место неравенства:

и .

Теорема (Чебышева). Если последовательно независимые случ. Величины и существует и для любого справедливо .