В.8. Степенные ряды в действительной и комплексной области. Радиус сходимости.

Опр.: Ряд вида (1) называется степенным рядом.

Т.(Абеля). Если степенной ряд (1) сх-ся при , то он сх-ся, и притом абсолютно, для всех , удовлетворяющих условию ; если ряд (1) расходится для всех , удовлетворяющих условию .

Т. Если ряд сходится при всех значениях и не только при x=0, то существует число R>0, такое что ряд абсолютно сх-ся при и рас-ся при .

Интервал (-R,R) называется интервалом сходимости степенного ряда. Число R называется радиусом сходимости.

Для ряда - радиус сходимости, - область сходимости.

Т. Если предел , то радиус сходимости ряда равен

Т. (интегрирование и дифференцирование степенных рядов)

Если функцию можно разложить в окрестности точки в степенной ряд с радиусом сходимости R>0, то:

1) Функция имеет на промежутке (-R,R) производные от всех порядков, которые м.б. найдены из (1) почленным дифференцированием (2);

2) Для справедливо тождество: (3);

3) ряды (1),(2),(3) имеют одинаковые радиусы сходимости.

Т. (выражение коэффициентов в степенные ряды ч/з его сумму)

Если функция раскладывается в некоторый окрестности в степенной ряд , то

.

Т.Если функцияна интервале (-R,R) разлагается в степенной ряд , то это разложение единственно.

Ряд вида называется рядом Маклорена функции.

Разложение в ряд Маклорена некоторых элементарных функций.

.

Ряд вида (4), где z – комплексная переменная; и - комплексные числа, называется степенным рядом.

Т.1) Если степенной ряд (5) сходится при , то он сх-ся и притом абсолютно, для всех z, удовлетворяющих условию ; 2) если ряд (5) расх-ся при , то он расх-ся для всех z, удовл. условию .

Т. Если ряд (5) сх-ся не при всех значениях z и не только при z=0, то существует число R>0 такое, что ряд сходится абсолютно при и расходится при

В.9. Ряд Фурье по ортогональной системе функций. Неравенство Бесселя, равенство Парсеваля, сходимость ряда Фурье.

Опр.: Пусть дана посл-ть, элементами кот-й явл-ся ф-ции (1) и определены в некоторой области . Такая посл-ть называется функциональной.

Опр.: Функциональный ряд вида (2) наз-ся тригонометрическим рядом.

Каждый член тригонометрического ряда – это ф-ция с периодом . Поэтому, если ряд (2) будет сходится, то его сумма будет периодическая с периодом .

Опр. Система функций называется ортогональной ситемой на , если выполняются 2 условия:

1) 2)

Т. Система функций является ортогональной системой на промежутке .

Любой бесконечно дифференцируемой функции соответствует ряд Тейлора.

Возьмём функцию , определённую на и сотавим с её помощью числа 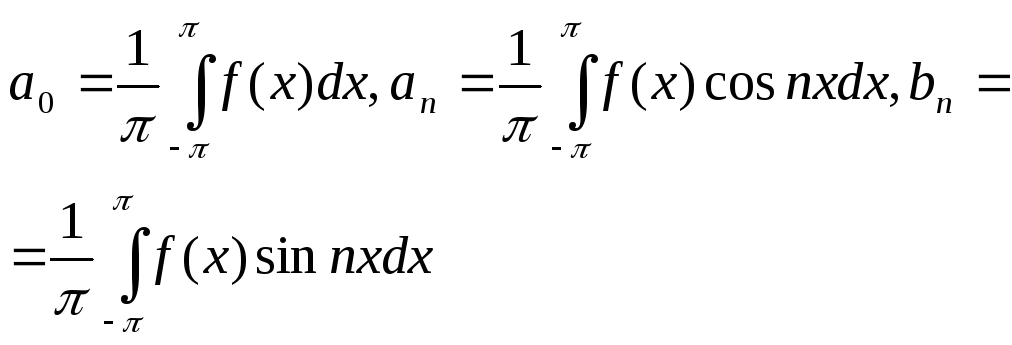(3)

Опр. Тригонометрический ряд, коэффициентами кот. служат числа (3) наз-ся рядом Фурье функции, а сами коэффициенты наз-ся коэф-ми Фурье функции .

Чтобы можно было вычислить коэф-ты Фурье, нужно предположить, чтобы функция была интегрируема на , след. каждой такой функции можно поставить в соответствие ряд Фурье. е

Утв. Если функциональный ряд сх-ся на и некоторая ограниченная на функция, то ряд также будет равномерно сходится на .

Т. Если функция разлагается на в равномерно сходящийся тригонометрический ряд есть её ряд Фурье.

Ряд Фурье четной и нечетной функции.

Пусть функция определена на и является четной: . Тогда её коэффициенты Фурье , .

Пусть определенная на - нечетная, т.е. . Тогда, , .

Сходимость ряда Фурье.

Будем говорить , что функция , определённая на всей числовой прямой и периодическая с периодом , является периодическим продолжением функции ; если на . Если на ряд Фурье сх-ся к функции , то он сх-ся на всей числовой прямой к её периодическому продолжению.

Т.Пусть функция и её производная - непрерывные функции на или же имеют на нём конечное число точек разрыва 1-го рода. Тогда ряд Фурье функции сх-ся на всей числовой прямой, причем в каждой точке , в которой непрерывна, сумма ряда равна , а в каждой точке разрыва функции сумма ряда равна , где и . На концах отрезка сумма равна . В любой точке сумма ряда Фурье равна , если x – точка непрерывности , и равна , если x – точка разрыва , где - периодическое продолжение функции .