
- •В.1.Предел и непрерывность функции одной и нескольких переменных. Свойства функций, непрерывных на отрезке.
- •Функции нескольких переменных.
- •1) Пусть дана последовательность, элементами которой являются функции (1) и определены в некоторой области . Такая последовательность называется функциональной.
- •2)Пусть . Рассмотрим посл-ть .
- •В.7. Производная функции комплексного переменного. Геометрический смысл аргумента и модуля производной. Условия Коши – Римана. Аналитическая функция.
- •В.8. Степенные ряды в действительной и комплексной области. Радиус сходимости.
- •В.9. Ряд Фурье по ортогональной системе функций. Неравенство Бесселя, равенство Парсеваля, сходимость ряда Фурье.
- •Ряд Фурье с периодом .
- •12. Вероятностное пространство. Случайные величины. Закон больших чисел в форме Чебышева.
- •В.13. Задача Коши для уравнения колебания струны. Формула Даламбера.
- •В.14. Постановка краевых задач для уравнения теплопроводности. Метод разделения переменных для решения первой краевой задачи.
В.1.Предел и непрерывность функции одной и нескольких переменных. Свойства функций, непрерывных на отрезке.
Пусть функция
![]() задана на множестве X
за исключением б.м. точки
задана на множестве X
за исключением б.м. точки
![]() .
Возьмем на множестве X
последовательность точек, отличных от
.
Возьмем на множестве X
последовательность точек, отличных от
![]() .
.
![]() (1).
Значения функций в этих точках также
образуют посл-ть:
(1).
Значения функций в этих точках также
образуют посл-ть:
![]() (2)
(2)
Опр.1:
Число A
называется пределом
функции
![]() в
точке
в
точке
![]() если для любой посл-ти точек (1) из X,
отличных от
если для любой посл-ти точек (1) из X,
отличных от
![]() и
сходящихся к
и
сходящихся к
![]() ,
посл-ть соот-их значений функции (2) сх-ся
к числу A.
,
посл-ть соот-их значений функции (2) сх-ся
к числу A.
![]() .
.
Опр.1.1:
Число A
называется пределом
функции
![]() в
точке
в
точке
![]() ,
если для любого
,
если для любого
![]() существует
существует
![]() из
нер-ва
из
нер-ва
![]()
![]() из
из
![]()
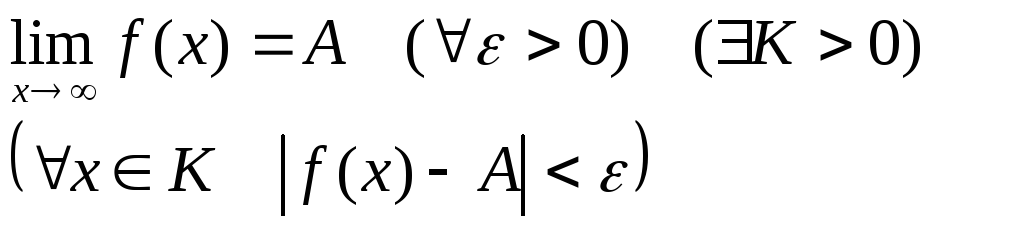
Опр.2.:Функция
![]() называется
непрерывной в точке
называется
непрерывной в точке
![]() ,если
выполняется тождество
,если
выполняется тождество
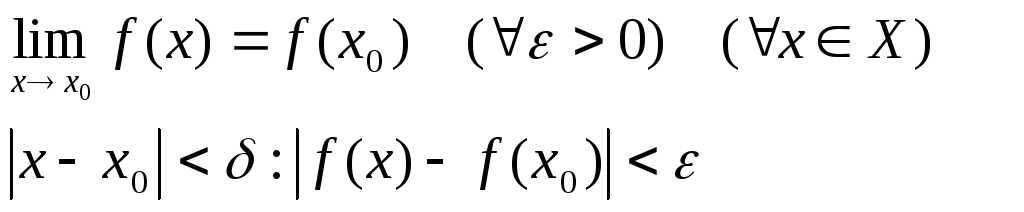
Рассмотрим
последовательномть точек
![]() .
Обозначается
.
Обозначается
![]() .
.
Пусть функция
![]() определена на некотором множестве
определена на некотором множестве
![]() и точка
и точка
![]() или
или
![]() ,
но обладает тем свойством, что в
,
но обладает тем свойством, что в
![]() окрестности этой точки содержится хотя
бы одна точка множества
окрестности этой точки содержится хотя
бы одна точка множества
![]() ,
отличная от
,
отличная от
![]() .
.
Опр.3.:Число
A
называется пределом
функции
![]() в
точке
в
точке
![]() ,
если для любой последовательности точек
,
если для любой последовательности точек
![]() соответствующая последовательность
значений функции
соответствующая последовательность
значений функции
![]() сх-ся к A.
сх-ся к A.
![]()
Опр.4.:
Функция
![]() называется непрерывной в точке
называется непрерывной в точке
![]() ,
если предел функции в этой точке сущ-ет
и равен значению функции в этой точке,
т.е.
,
если предел функции в этой точке сущ-ет
и равен значению функции в этой точке,
т.е.
![]() или
или
![]() .
.
Свойства функций непрерывных на отрезке.
1)Т.
Больцано – Коши.
Пусть на отрезке
![]() задана непрерывная функция
задана непрерывная функция
![]() .
Причем на концах отрезка она имеет
значения разных знаков. Тогда на
.
Причем на концах отрезка она имеет
значения разных знаков. Тогда на
![]() существует по крайней мере одна точка
существует по крайней мере одна точка
![]() .
.
2) 2-я
Т. Больцано – Коши.
Пусть на
![]() определена непрерывная функция
определена непрерывная функция
![]() ,
принимающая на концах отрезка различные
значения
,
принимающая на концах отрезка различные
значения
![]() тогда какое бы число C
находящееся между A
и B
мы ни взяли, на
тогда какое бы число C
находящееся между A
и B
мы ни взяли, на
![]() найдется такое число c,
что
найдется такое число c,
что
![]() .
.
3) Т.
Вейерштрасса.
Если функция
![]() непрерывна на
непрерывна на
![]() ,
то она ограничена на
,
то она ограничена на
![]() ,
т.е. существует
,
т.е. существует
![]() и
и
![]() .
.
4) 2-я
Т. Вейерштрасса.
Пусть функция
![]() непрерывна
на
непрерывна
на
![]() .
Тогда среди всех значений есть наибольшее
и наименьшее значение.
.
Тогда среди всех значений есть наибольшее
и наименьшее значение.
Замечательные
пределы:
![]()
![]()
![]()
В.2. Производная и дифференциал функции одной и нескольких переменных. Необходимые и достаточные условия дифференцируемости.
Пусть функция
![]() определена в промежутке X.
Исходя из некоторого значения
определена в промежутке X.
Исходя из некоторого значения
![]() независимой
переменной, придадим ему приращение
независимой
переменной, придадим ему приращение
![]() ,
не выводящее его из промежутка X,
так что и новое значение
,
не выводящее его из промежутка X,
так что и новое значение
![]() .
Тогда
.
Тогда
![]() заменится новым значением
заменится новым значением
![]() ,
т.е.
,
т.е.
![]() .
.
Опр.:
Если существует предел отношения
приращения функции
![]() к вызвавшему его приращению независимой
переменной
к вызвавшему его приращению независимой
переменной
![]() ,
при стремлении
,
при стремлении
![]() к 0,т.е.
к 0,т.е.
![]() ,
то он называется производной
функции
,
то он называется производной
функции
![]() по независимой переменной x
при данном её значении (или в данной
точке)
по независимой переменной x
при данном её значении (или в данной
точке)
![]() .
.
Пусть имеем функцию
![]() ,
определённую на X
и непр. в точке
,
определённую на X
и непр. в точке
![]() .
Тогда приращению
.
Тогда приращению
![]() аргумента отвечает приращение
аргумента отвечает приращение
![]() ,
беск. малое вместе с
,
беск. малое вместе с
![]() .
При А=0 наличие равенства
.
При А=0 наличие равенства
![]() (1) показывает, что беск. малая
(1) показывает, что беск. малая
![]() (линейная
относительно
(линейная
относительно
![]() беск. малая,
беск. малая,
![]() ) эквивалентна беск.малой
) эквивалентна беск.малой
![]() и значит служит для последней её главной
частью, если за основную беск.малую
взять
и значит служит для последней её главной
частью, если за основную беск.малую
взять
![]() .
.
Опр.:
Дифференциалом
функции
![]() в точке
в точке
![]() называется главная линейная относительно
называется главная линейная относительно
![]() часть приращения функции в этой точке:
часть приращения функции в этой точке:
![]() .
.
Формула Лейбница
для n-ой
производной произведения 2-х функций:
![]()
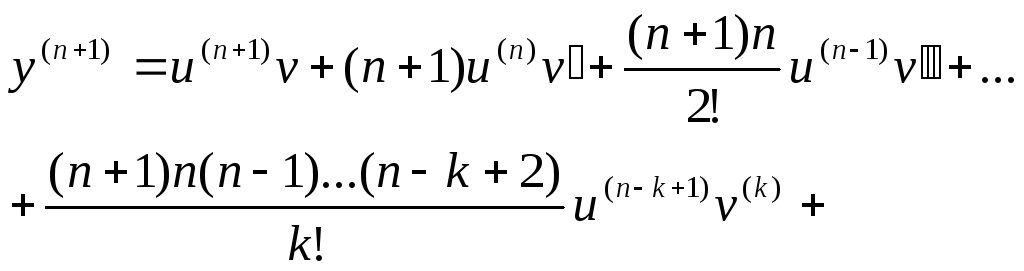
…![]()
![]() Для
n-го
дифференциала функции справедлива
формула
Для
n-го
дифференциала функции справедлива
формула
![]() .
.
Утверждение: Для
того чтобы функция
![]() в точке
в точке
![]() была дифференцируема , Н. и Д., чтобы для
неё в этой точке существовала конечная
производная
была дифференцируема , Н. и Д., чтобы для
неё в этой точке существовала конечная
производная
![]() .
При выполнении этого условия равенство
(1) имеет место при значении постоянной
A,
равной именно этой производной:
.
При выполнении этого условия равенство
(1) имеет место при значении постоянной
A,
равной именно этой производной:
![]()
