Теория вероятностей и математическая статистика
Лекция 6
1 курс. 4 зач.ед.
144 часа (36 час. лекц., 36 час. практич. зан.,
72 час. самост. раб.). Экзамен.
1
Теория вероятностей и математическая статистика
5. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ. 5.1. Случайная величина
Случайной величиной называется величина, которая в результате испытания может принимать то или иное заранее неизвестное значение из множества ее возможных значений.
2
Теория вероятностей и математическая статистика
5. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ. 5.1. Случайная величина
Случайной величиной называется величина, которая в результате испытания может принимать то или иное заранее неизвестное значение из множества ее возможных значений.
3
Теория вероятностей и математическая статистика
Случайные величины обозначают прописными буквами X, У, Z, а их возможные значения — соответствующими строчными буквами х, у, z.
Например, если случайная величина X имеет три возможных значения, то они будут обозначены так: х1, х2,
х3.
4
Теория вероятностей и математическая статистика
Различают случайные величины, принимающие лишь отдельные, изолированные значения, и случайные величины, возможные значения которых сплошь заполняют некоторый промежуток.
5
Теория вероятностей и математическая статистика
Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями.
Число возможных значений дискретной случайной величины может быть конечным или бесконечным.
6
Теория вероятностей и математическая статистика
Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями.
Число возможных значений дискретной случайной величины может быть конечным или бесконечным.
7
Теория вероятностей и математическая статистика
Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями.
Число возможных значений дискретной случайной величины может быть конечным или бесконечным.
8
Теория вероятностей и математическая статистика
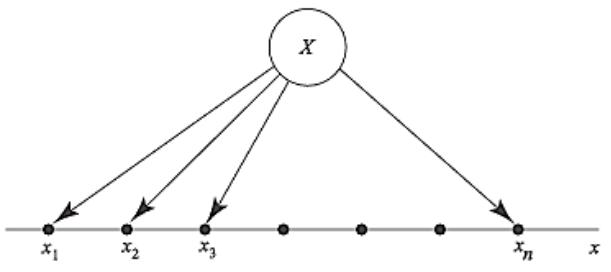
Пример дискретной случайной величины
Число очков, выпадающих при однократном бросании игральной кости, - случайная величина Х.
Множество ее возможных значений: х1, х2, х3, х4, х5, х6.
Дискретная случайная величина
9
Теория вероятностей и математическая статистика
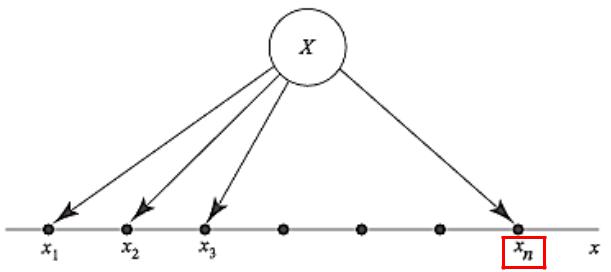
Пример дискретной случайной величины
Число очков, выпадающих при однократном бросании игральной кости, - случайная величина Х.
Множество ее возможных значений: х1, х2, х3, х4, х5, х6.
Дискретная случайная величина
10