Добавил:

SGUPSik Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирский Государственный Университет Путей Сообщения

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

шпаргалка по интегралам

.pdf

Скачиваний:

Добавлен:

16.06.2022

Размер:

213.1 Кб

Скачать

☆

Неопределенный интеграл

№

Новое понятие

Содержание

п/п

совокупность всех первообразных F(x) для функции f(x) на промежутке (a; b),

неопределённый интеграл

f (x)dx F (x) C , где

— знак неопределённого интеграла, функция f(x) —

от функции f (x)

подынтегральная функция, выражение f (x) dx — подынтегральное выражение,

С — произвольная постоянная

0 du C ;

[1]

du u C ;

[2]

u n du

u n 1

C, n 1;

[3]

n 1

ln|u| C ;

[4]

au du

C,a 0,a 1;

[5]

lnа

eu du eu

C ;

[6]

sinu du cosu C ;

[7]

таблица простейших

cosu du sinu C ;

[8]

интегралов

ctg u C ;

[9]

sin

tg u C ;

[10]

cos

arcsin u

a u a, a 0;

[11]

ln|u

u 2 a 2| C ;

[12]

u a

a 0;

[13]

u a

1 arctg u

a 0;

[14]

Основные методы интегрирования

метод непосредственного

интеграл путём тождественных преобразований подынтегральной функции

(или выражения) и применения свойств неопределённого интеграла

интегрирования

приводится к одному или нескольким табличным интегралам

подведение под знак

f (x) (x)

dx f (t) dt

дифференциала

правило поправочного

f (a x

b) dx

F (a x

b) C (a, b — const)

коэффициента

- 1 -

		u и v — две функции аргумента х, имеющие производные u						и v
			u dv u v v du

		вид интеграла			u
		P(x) a bx	dx ; P(x) sin kx dx ;	u=P(x)
		P(x) coskx dx		u=P(x)
		P(x) coskx dx

		P(x) ln Q(x) dx ;
	интегрирование	P(x) arcsin(mx) dx ;		ln(Q(x));
3	интегрирование
3	по частям
	по частям	P(x) arccos(mx) dx ;		u= arcsin(mx); arccos(mx);
		P(x) arctg(mx) dx ;		arctg(mx); arcctg(mx);

		P(x) arcctg(mx) dx

		возвратные		sin( x );		или u=e kx
		e kx sin( x ) dx ; e kx cos( x ) dx		u=	).	или u=e kx
			a x 2 dx	cos( x	).
			a x 2 dx	u	a x		2
				u	a x

1.Определить вид дроби, для интегрирования простейших дробей

воспользоваться соответствующей формулой:

	dx	ln \| x a \| C	или		dx		(x a) k 1	C
	x a				(x a)k		k 1

2.Если числитель является дифференциалом знаменателя, то воспользоваться способом подведения под дифференциал;

3.Если дробь неправильная, то представить её в виде суммы многочлена и правильной дроби (выделить целую часть);

4.Если дробь правильная, то, разложив знаменатель правильной рациональной дроби на множители; представить дробь в виде суммы простейших рациональных дробей;

вид множителя

вид слагаемого

х – а

x a

(x a)k

...

(x a)k

x-a (x a)2

p x q

C x D

x2 p x q

интегрирование рациональных

p x q)

M1x

...

M k x Nk

x2 px q

px q k

дробей

Если

дробь

Cx D

то в

знаменателе

выделить полный

x2 px q

квадрат

сделать

замену

t x

перейти к

сумме

двух

интегралов, т.е.

Cx D

ln | x2

px q |

arctg

px q

Mx N

Если

дробь

px q k

то

воспользоваться

формулой:

Mx N

t dt

dx =M

x2 px q

(t 2

a 2 )k

2 a 2 )k

I k ,

где

a 2

p 2

2(1 k)(t 2

a 2

)k 1

2k 3

(t 2 a 2 )k

2 (k

(t 2 a 2

)k 1

a 2

2k 2

k 1

- 2 -

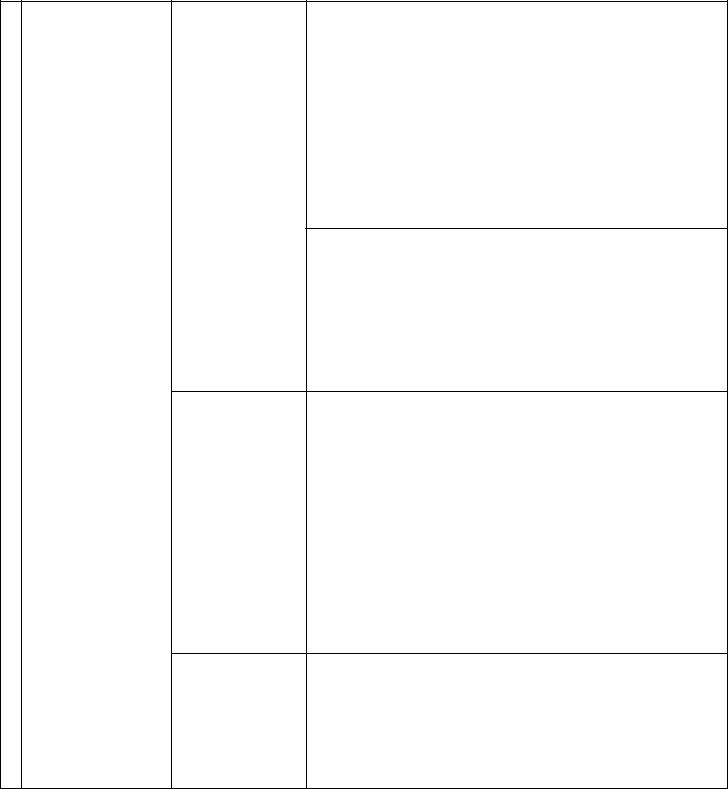
интегрирование 3 тригонометрических

функций

sin x cos x

sin( )x sin( )x ;

sin x cos x dx ;

cos x cos x dx ;

cos x cos x

cos( )x cos( )x ;

sin x sin x dx

где

sin x sin x

cos( )x cos( )x .

универсальная тригонометрическая подстановка

t tg

; x 2arctg t;

2 dt

;

1 t 2

sin x =

; cos x

t 2

если R (– sin x; cos x) = – R(sin x; cos x) – нечётна

R(sin x;cos x) dx	относительно sin x, то
	t = cos x, dt = – sin x dx; sin2 x 1 t 2 ,	cos2x 2t 2	1;

если R (sin x; – cos x) = –R (sin x; cos x) – нечётна относительно cos x, то

t = sin x, dt = cos x dx; cos2 x 1 t 2 ;

если R (–sin x; – cos x) = R (sin x; cos x) – чётная функция, то

t = tg x; x=arctg x; dx	dt	; sin2 x	t 2	; cos2 x	1
	t 2		t 2		1 t 2
1		1

k, n — хотя бы одно число нечётное

отделить от нечётной степени один множитель и подвести его под знак дифференциала;

k, n — чётные положительные

воспользоваться формулами понижения степени:

	sin x cos x	1	sin 2x ; sin2	x	1 cos2x	;	cos2 x	1 cos2x	;
								2
	2			2
sink x cosn x dx	k, n — нечётные положительные
	отделить от наименьшей степени один множитель и подвести его под
	знак дифференциала;

n — целое положительное число

применить подстановку t = sin x;

k — целое положительное нечётное число

применить подстановку t = cos x;

n+k — чётное отрицательное целое число

применить подстановку t = tg x

	если n = 1, то tgx dx	ln \| cos x \|			C , ctgx dx		ln \| sin x \| C
	если n >1, то tg2 x	1		1;	ctg 2 x	1		1, т.е. понизить
tgn x dx ,		cos2				sin2
			x				x
ctg n x dx	степень тангенса или	котангенса непосредственно, отделяя один
	множитель и подводя его под знак дифференциала

- 3 -

вид интеграла

подстановка (формула)

1. если числитель есть производная подкоренного

трёхчлена,

то

следует

сделать

замену

t ax2

bx c , что приводит исходный интеграл к

виду dt 2

t C ;

2. если числитель не зависит от х, т.е. М = 0, то под

знаком радикала выделим полный квадрат из

квадратного трёхчлена, в результате чего получим

Mx N

квадратный

двучлен, в

зависимости

от

знака а

исходный интеграл

сводится

одной

из

формул:

bx c

arcsin a C

[11]

или

a 2 u 2

ln|u

u 2

a 2| C [12];

2 a 2

если

M 0, то

под

знаком

радикала

выделив

полный квадрат, сделать подстановку t x

b , при

этом исходный интеграл разбивается на сумму двух

интегрирование

интегралов

иррациональных функций

m ax b

ax b

ax b t

т.е. t

R x,

,...,

cx d

m — наименьшее общее кратное чисел q,…,t

где R — рациональная функция;

p, q, …,s, t — целые числа

x a sin t;

dx a cost dt

R x,

a 2

x 2

или

x a cost;

dx a sin t dt

x a tgt;

dx a dt

R x,

cos2 t

a 2

x 2

или

x a ctgt;

a dt

sin2

; dx a sint dt

R x,

a2 dx

cost

cos2 t

или

;

a cost dt

sin t

sin2

sin

cos

ctg

sin

1 sin2

sin

связь между

cos

1 cos2

cos

1 cos2

cos

1 cos2

тригонометрическими

функциями

1 tg 2

1 tg

ctg

1 ctg 2

ctg

- 4 -

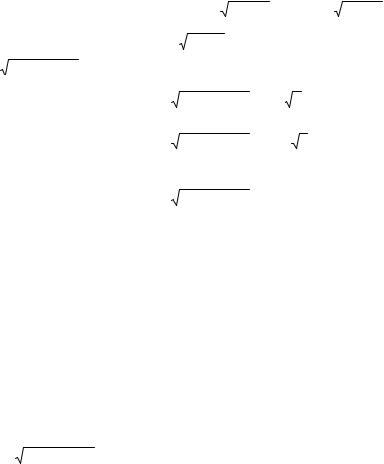
выделив под радикалом полный квадрат и

сделав

подстановку

t x

интегралы

указанного вида приводятся к интегралам вида:

R x, a2 x2

dx , R x,

a2 x2 dx ,

R x,

x2 a2 dx

R(x; ax

bx c )dx

Подстановки Эйлера

если

a>0,

подстановка

ax 2 bx c t a x ;

если

с>0,

подстановка

ax 2 bx c xt c ;

если

ах2+bx+c

имеет

различные

действительные

корни

х1

х2,

подстановка

ax 2 bx c t(x x1 )

р — целое число,

подстановка

x t k , где k

— наименьшее общее

кратное дробей m и n;

m 1

— целое число,

x m (a bx n )p dx

подстановка

a bx n t s , где s — знаменатель дроби

m 1

p — целое число,

подстановка

a bx n

x n t s ,

где

—

знаменатель

дроби р

(Mx N ) dx

подстановка x

; dx

t 2

(x )

ax 2 bx c

- 5 -

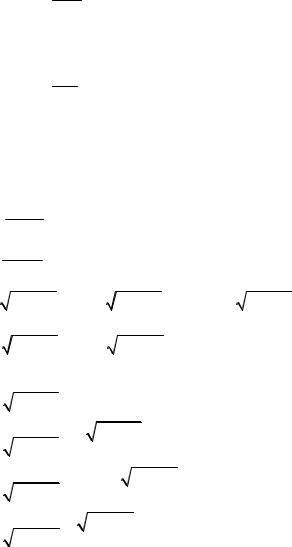
0 du C ;

du u C ;

un 1

undu n 1 C ; n R /{ 1}

duu ln|u | C ;

au du au C ; lnà

eu du eu C ;

sinu du cosu C ;

cosu du sinu C ;

sindu2 u ctg u C ;

cosdu2 u tg u C ;

u2 a2 du u

u2 a2 a2

u u2 a2

a2 u

du u

a2 u2 a2

arcsin u

C ;

arcsin u

C ;

u du

a2 u2 C ;

ln|u u2 a2 | C ;

u du

a2 C ;

u a

C ;

u2 a2

u a

u du

2ln|u

| C ;

u2 a2

a arctg a

C ;

a2 u2

u du

2ln|a

| C ;

a2 u2

tg u du sinu du ln|cosu | C ;

cosu

ctg u du cosu du ln|sinu | C ;

sinu

C ;

sinu

C ;

cosu

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

- 6 -

функции

производная

дифференциал

(u v) u v

d (u v) du dv

[1]

u v u v

u v

C u

d (u v) v du u dv

[2]

Основные

арифметические

операции

u v u v

vdu

udv

[3]

C v

n 1

n un 1d u

[4]

R \{

d u

[5]

2 u

d u

[6]

y au

y au lna u

d au au lna d u

[7]

y eu

y eu u

d eu eu d u

[8]

y loga u

d loga u

d u

[9]

u lna

y lnu

d lnu

d u

y u

[10]

y sinu

y cosu u

d(sinu) cosu d u

[11]

y cosu

y sin u u

d(cosu) sin u du

[12]

y tg u

d u

y cos2u

d(tg u) cos2u

[13]

y ctg u

d u

y sin2 u u

d(ctg u) sin2 u

[14]

y arcsinu

d(arcsinu)

d u

[15]

1 u2

y arccosu

d(arccosu)

d u

[16]

1 u2

y arctg u

d u

y 1 u2

d(arctg u)

1 u2

[17]

y arcctg u

d u

y 1 u2 u

d(arcctg u) 1 u2

[18]

- 7 -

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
24.01.202251.89 Кб30РЕФЕРАТ ПО ИСТОРИИ.docx
#
24.01.202243.01 Кб16РЕФЕРАТ ПО РУССКОМУ.docx
#
24.01.202256.95 Кб27РЕФЕРАТ ПО ФИЛОСОФИИ.docx
#
24.06.202216.44 Mб20термех ЭКЗ ВОПРОСЫ.docx
#
19.12.20241.62 Mб5транспортный бизнес лекции+тест.pdf
#
16.06.2022213.1 Кб29шпаргалка по интегралам.pdf
#
28.02.20251.25 Mб0экз ауэр.pdf
#
28.02.20258.12 Mб1экз нтп.pdf
#
28.02.2025521.14 Кб1экз экология.pdf