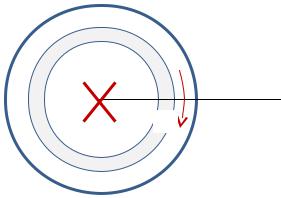
Flux linkage of a thin current layer
Consider a thin cylinder with the radius of r and the thickness of dr
The current inside this layer is
di |
i |
2 r dr |
2irdr |
|
R2 |
R2 |
|||
|
|
i |
dr R |
|
r |
||
|
The flux linkage per unit length:
R |
R |
i r |
|
|
|
|
|
|
|
|
int (r) B(r) dr |
|
|
dr |
|
|
|
|
|
||
|
|
2 |
|
|
|
|
|
|||
|
|
2 R |
|
|
|
|
|
|
||
r |
r |
|
|
|
|
|
|
|
||
|
|
|
|
(r) i |
|
r |
2 |
|
||
After integration: |
|
|
|
1 |
|
|
|
|||
|
int |
|
|
2 |
||||||
|
|
|
4 |
|
R |
|
||||
|
|
|
|
|
|
|
|
|||
21
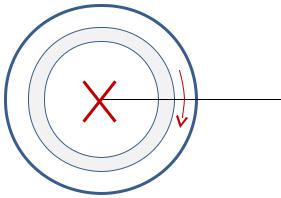
Flux linkage of a thin current layer
The flux linkage of a thin layer:
d di |
|
|
di i |
|
r |
2 |
|
||
|
|
1 |
|
|
|
||||
int |
|
|
2 |
||||||
int |
i |
|
4 i |
|
R |
|
|||
|
|
|
|
|
|
||||
Total internal flux linkage:
|
R |
|
|
R |
r |
2 |
|
2ir dr |
||
d |
1 |
|
|
|
||||||
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
int |
|
int |
4 |
|
R |
2 |
|
R |
2 |
|
|
0 |
|
||||||||
|
0 |
|
|
|
||||||
dr |
r |
|
B |
|
|
|
i |
R |
r |
2 |
|
i |
R |
|
i |
R |
r3dr |
||||||
|
|
|
|
1 |
|
|
rdr |
|
|
rdr |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
or: |
int |
|
2 R |
2 |
|
R |
2 |
2 R |
2 |
|
2 R |
4 |
|
||||||
|
|
|
|
|
|||||||||||||||
|
|
|
|
0 |
|
|
0 |
|
|
0 |
|
||||||||
22
Internal inductance of a thin conductor
Transformation of the last integral:
|
|
|
i |
R rdr |
i |
R r3dr |
|
|
i |
1 r2 |
|
|
|
1 |
|
|
r 4 |
R |
|
||||||||||||
|
2 |
4 |
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|||||||||||||||||
int |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
2 R 0 |
|
|
2 R 0 |
|
|
|
2 R 2 |
|
|
|
|
4R |
|
|
|
0 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
Taking into account the limits: |
|
|
|
i |
|
1 |
|
R2 |
|
|
|
1 |
R4 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||||||||||||||||
|
|
int |
|
2 R |
2 |
|
2 |
|
|
|
|
|
4R |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Final expression: |
|
|
|
|
|
|
|
int |
i |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Internal inductance: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
int |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Lint |
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
i |
|
|
|
|
|
|
|
int |
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
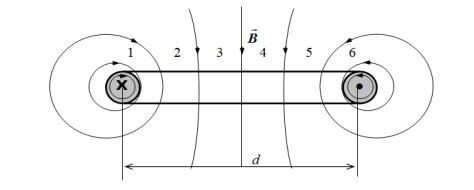
External inductance of two-wire transmission line
Flux density induced be a wire:
B(r) i 0
2 r
External flux:
1ext |
i 0 |
d dr |
|
i 0 |
ln |
d |
R – radius of the wire; R << d |
|
2 |
R r |
2 |
R |
|||||
|
|
|
|
Similar flux is induced by the second wire.
The total external flux: |
ext i 0 |
ln |
d |
|
R |
||||
|
|
|
24
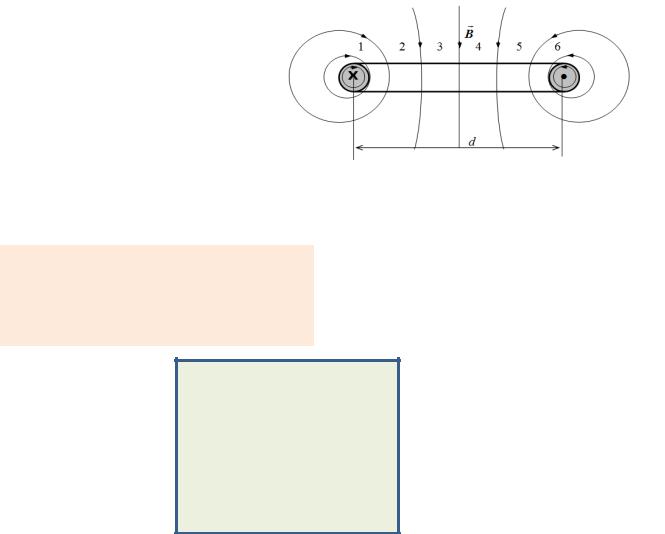
Inductance of a two-wire transmission line
Flux linkage:
|
1 |
|
d |
|
r |
|
ext 2 int i 0 |
|
ln |
|
|
|
|
|
R |
|
||||
|
|
|
4 |
|||
|
|
1 |
ln |
d |
|
r |
|
Inductance: |
L 0 |
|
|
|
|
|
|
|
R |
|
|||||
|
|
|
|
4 |
|||
Internal inductance: |
Lint |
|
|
|
|
||
4 |
|
|
d |
||||
|
|
|
|
|
|||
External inductance: |
L |
0 |
|
ln |
|||
|
|
||||||
ext |
|
|
|
R |
|||
|
|
|
|
|
|||
25