Vector magnetic potential
Main equations:
divB 0 |
B H |
curl H J |
|
|
Consider a vector A satisfying a relation: |
|
|||
|
|
|
|
|
|
|
B curl A |
|
|
|
|
|
div curl A 0 |
|
The equation for the flux density will be |
||||
satisfied |
automatically : |
|
|
|
div B 0
A- Vector magnetic potential
11
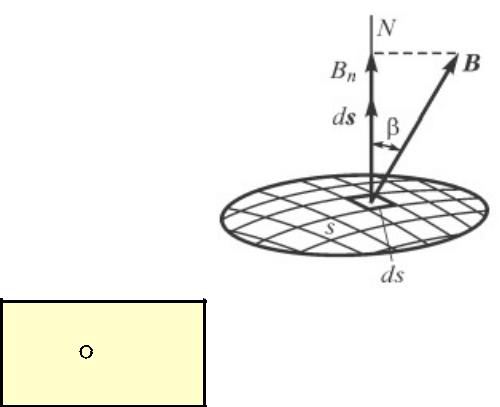
Magnetic flux
Definition of the flux
|
|
|
B ds |
|
|
S |
|
|
curlA |
||
ds |
||
S |
(Stokes theorem) |
|
|
Adl
l
12
Differential equation for the
Vector magnetic potential
Ampere’s Law: |
curl H J |
|
|
|
1 |
|
|||
|
|
|
|
|
|||||
Magnetic field intensity and flux density are related by: |
|
H |
|
|
B |
||||
|
|||||||||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
Taking into account B curl A , |
|
|
1 |
|
|
|
|
|
|
we get: |
curl |
|
curlA J |
|
|||||
|
|
||||||||
For the constant magnetic permeability: |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|||
curl curlA J |
|
|
|
|
|
|
|
||
Identical transformation: |
curl curlA grad divA 2 A |
||||||||
grad divA 2 A J
13
Gauging of the vector magnetic potential
The vector potential defined by the relation B curl A is not unique
.
Adding a term of F grad to the value of the vector potential does not change the flux density, because
curl grad 0
The choice of the exact adding is called gauging
The most often ‘Coulomb gauging’ is used
divA 0
14
Integral presentation of the vector magnetic potential
For the Coulomb gauging of the vector |
grad divA 2 A J |
|
potential we get |
|
|
|
|
|
|
2 A J |
|
|
|
|
In Cartesian coordinate system this vector equation results in 3 scalar ones:
Ax J x |
A J |
y |
Az J z |
y |
|
compare: |
U |
|
|
|
|||
|
|||
|
|
15
Integral presentation of the vector magnetic potential
Each scalar equation has an integral solution of:
Ax |
0 |
|
J xdV |
Ay |
0 |
|
J y dV |
A |
|
|
0 |
|
J |
dV |
|
|
|
|
|
|
|
z |
|
||||||
4 |
|
4 |
|
|
|
|||||||||
|
|
4 |
|
|
||||||||||
|
r |
|
r |
z |
|
r |
||||||||
compare:
We can unite these expressions into one vector formula:
U |
1 |
|
dV |
4 |
|
||
|
r |
||
|
0 |
JdV |
A |
||
|
|
r |
|
4 |
16
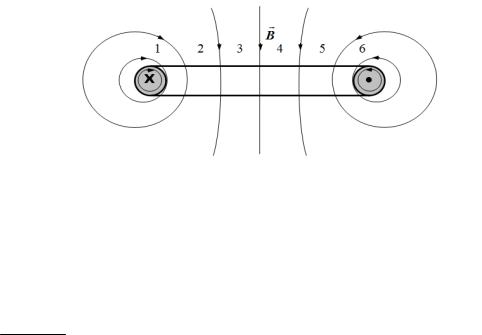
Inductance.
Inductance is a coefficient between the current and the flux linkage.
L i
Units: Henry [Hn]
The magnetic energy stored in a coil is derived as
Wm L i2
2
17
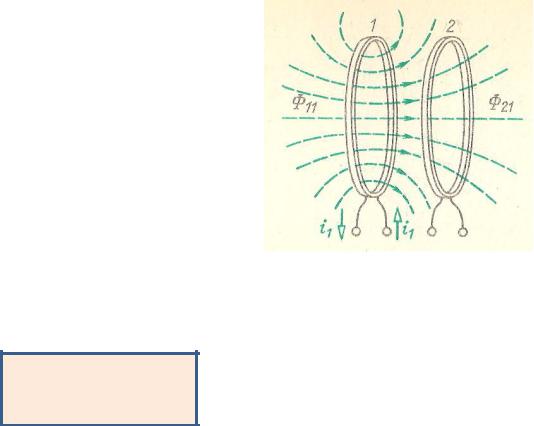
Mutual inductance.
A coefficient between the current in one coil and a flux (flux coupling) in another coil is called a ‘mutual inductance’
21 M 21 i1
Reciprocity principle |
(принцип взаимности): |
M12 M 21
18
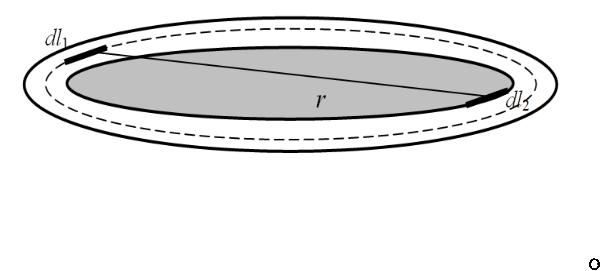
Inductance of thin contours
The inductance may be split in two parts – external and internal
External flux definition: |
ext ext A2dl2 |
|
l2 |
19
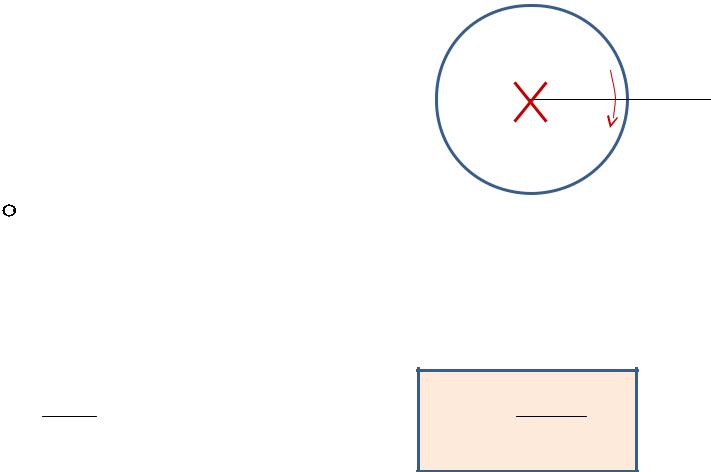
Field intensity inside a cylindrical conductor
Infinitely long cylindrical wire with the radius of R, and the
current of i
The field intensity inside the conductor at the point |
i |
r |
||||
H |
||||||
|
||||||
with the radius of |
r |
satisfies |
the Ampere Law |
|
||
|
Hdl i |
|
|
|
||
Directions of the intensity vector and dl vector are he same. |
|
|
||||
|
|
H 2 r J r 2 |
|
|
||
Current density: |
J |
i |
Field intensity: |
H i r |
||
|
|
R2 |
|
|
2 R2 |
|
20