Матмод-экзамен

Обозначим pi(t) — вероятность того, что в момент t система S будет находиться в состоянии Si (i= 1, ..., n). Очевидно, для любого момента t сумма вероятностей состояний равна единице:

(0-5)

так как события, состоящие в том, что в момент t система находится в состояниях S1, S2,, ..., Sn , несовместны.

Необходимо определить для любого t вероятности состояний:

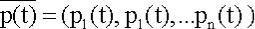(0-6)

Для того чтобы найти эти вероятности, необходимо знать характеристики процесса, аналогичные переходным вероятностям для Марковской цепи. В случае процесса с непрерывным временем вместо переходных вероятностей Pij рассматриваются плотности вероятностей (или интенсивности) перехода λij (поскольку вероятность перехода системы из состояния в состояние точно в момент t будет равна нулю, так же, как вероятность любого отдельного значения непрерывной случайной величины).

Выходными характеристиками марковского процесса с дискретным множеством состояний и непрерывным временем являются:

нестационарное распределение вероятностей ;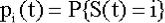

стационарное распределение вероятностей ;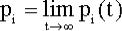

среднее время пребывания в фиксированном множестве состояний;

интенсивности перехода из одного множества состояний в другое.

Марковская последовательность называется стационарной, если она однородна и все состояния хi имеют одну и ту же безусловную ПРВ w(х).

10. Марковская модель процесса восстановления работоспособности техники связи

Полумарковский процесс или, как его иногда называют, процесс марковского восстановления сочетает в себе свойства марковских процессов и процессов восстановления. Полумарковский процесс – это такой случайный процесс, который переходит из одного состояния в другое в соответствии с заданными распределениями вероятностей, а время пребывания процесса в каком-либо состоянии является случайной величиной, распределение которой зависит как от этого состояния, так и от состояния, в которое будет осуществлен следующий переход процесса.

Процесс восстановления, цепь Маркова с дискретным временем и однородный Марковский процесс с непрерывным временем являются частными случаями полумарковского процесса. Так, процесс восстановления – полумарковский процесс с одним состоянием. Марковская цепь с дискретным временем

– полумарковский процесс, у которого длительности пребываний в каждом из состояний равны единице, а однородный Марковский процесс с непрерывным временем есть полумарковский процесс, у которого время пребывания в каждом состоянии имеет показательное распределение, зависящее лишь от номера этого состояния.

Причём, распределения P{ 0 0} 1 , pi P{ 0 i} 0 , pi 1.

i E

Марковская цепь задаётся переходными вероятностями, которые называются полумарковским

ядром:

P{ n 1 j, n 1 t n i, n } P{ n 1 j, n 1 t n i} Qij (t) .

Будем предполагать, что эта переходная вероятность не зависит от n (номера шага), это означает однородность марковской цепи.

Полумарковское ядро - вероятность того, что полумарковский процесс перейдёт в состояние j и время до этого перехода не превзойдёт t при условии, что процесс пребывает в состоянии i.

5)Qij (t) является неубывающей функцией, аналогично Fij (t) .

6)p 1, i E {1,2,..., N} .

j E ij

Вероятности переходов в моменты скачков определяются стохастической N N матрицей P pij

, которая задаёт вложенную цепь Маркова, где pij - вероятность перехода из состояния i в состояние j . Если процесс из состояния i перейдёт в состояние j , то время пребывания процесса в состоянии i не превосходит t и из состояния i процесс переходит в состояние j .

Последовательность построения полумарковского процесса:

1.Определение Марковских моментов.

2.Определение состояний процесса.

3.Вычисление полумарковского ядра Qij (t) .

4.Проверка свойств полумарковского ядра.

11.Стохастические сети и их элементы. Понятие эквивалентной функции

Стохастическая сеть – совокупность взаимоувязанных узлов (вершин) и ветвей, соединение которых соответствует алгоритму.

Как следует из определения, стохастическая сеть состоит из вершин (узлов) и ветвей. Вершина стохастической сети характеризуется вероятностью ее реализации и может быть интерпретирована как

состояние системы. Поскольку стохастическая сеть является двухполюсной, то ее вершины подразделяются на входную, выходную и промежуточные (внутренние). Каждая промежуточная вершина сети состоит из входной (приемной) и выходной (распределительной) частей, отображающих те, или иные логические операции. В настоящее время используются 3 вида входных («И», «ИЛИ» и «Иск. ИЛИ») и 2 выходных («детерминированный» и «вероятностный») частей вершин. Графическое представление различных типов вершин показано в таблице

Входная часть вершины определяет условие (логическую операцию), при котором она может быть выполнена.

Выходная часть определяет совокупность условий, определяющих возможность выполнения данной вершины. Другими словами, выходная функция показывает, все ли исходящие из вершины ветви должны быть выполнены, или только одна из них.

Рассмотрим указанные типы вершин более подробно:

«Исключающее ИЛИ» - предусматривает реализацию вершины при выполнении любой ветви, входящей в данную вершину. При этом, одна и только одна ветвь может быть реализована в заданный момент времени.

«Включающее ИЛИ» – реализация любой ветви, входящей в вершину приводит к ее реализации. Временем ее реализации является минимальное время свершения подпроцессов, соответствующих любой из входящих ветвей.

«И» – данная вершина будет реализована только тогда, когда все входящие в нее ветви реализуются. Время реализации такой вершины соответствует максимальному времени свершения подпроцессов, соответствующих всем входящим ветвям.

«Детерминированный выход» - в случае реализации вершины, используются все исходящие из нее ветви. Все ветви, начинающиеся от этой вершины, реализуются с вероятностью равной единице.

«Вероятностный выход» - при реализации вершины, в лучшем случае используется одна исходящая ветвь.

Эквивалентная функция – полученная с использованием уравнения Мейсона преобразования Лапласа случайного закона времени реализации стахостической сети.

Понятие эквивалентной функции стохастической сети

Рассмотрим сеть G = (N,A). Вершины данной сети образуют множество N, а ветви - множество A. Пусть время реализации ветви aij, соединяющей i и j вершины есть случайная величина tij. Понятно, что ветвь aij может быть реализована только в том случае, если будет выполнена вершина i. Следовательно, необходимо знать условную вероятность (в дискретном случае) или плотность распределения (в непрерывном случае) случайной величины tij при условии, что вершина i выполнена.

Положим fij(t) - условная вероятность или плотность распределения времени реализации ветви aij , а преобразование Лапласа, совпадающее с характеристической функцией случайной величины tij определяется как [16,17]

Обозначим pij – вероятность того, что ветвь aij будет реализована при условии выполнении вергшины i. Тогда для представленного стохастической сетью случайного процесса эквивалентная функция Qij(s) определяется по формуле:

(15)

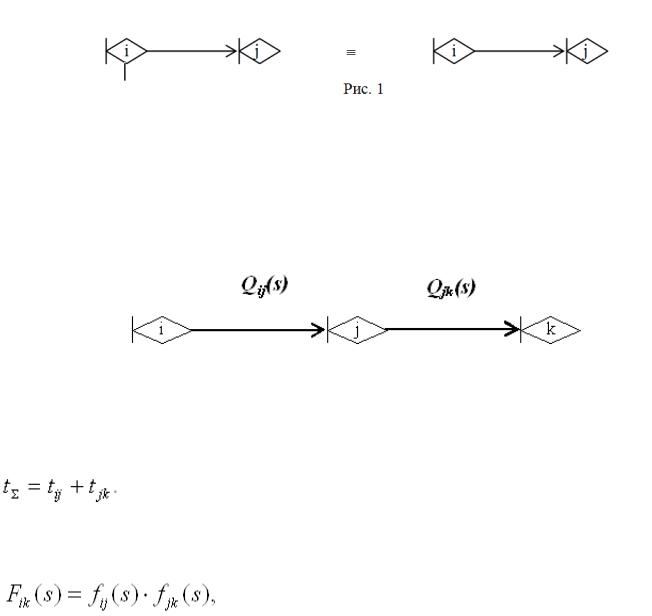
То есть ф(15) ставит в соответствие исходной стохастической сети G эквивалентную ей сеть G ‘, которая характеризуется всего одним параметром – эквивалентной функцией Qij(s), (рис.1).

12. Последовательное соединение ветвей стохастической сети

Последовательное соединение ветвей стохастической сети на примере фрагмента стохастической сети, изображённой на рисунке, ветви которой характеризуются эквивалентными функциями Qij(s) и Qjk(s).

По существу, фрагмент соответствует случайному процессу, состоящему из двух последовательно протекающих подпроцессов, каждый из которых реализуется за некоторое случайное время. Пусть времена реализации равны tij и tjk. Тогда, суммарное время реализации будет равно

В свою очередь, преобразование Лапласа функции плотности вероятностей времени tå равно произведению преобразований соответствующих функций плотности, т.е. [6,7]

а вероятность совместной реализации этих двух подпроцессов pik=pij·pjk.

Отсюда Qå(s)=Qik(s)=pij•fij(s)•pjk•fjk(s)=Qij(s)•Qjk(s). То есть, последовательное соединенные ветви сохраняют связность входной и выходной вершин сети. Поэтому последовательное соединение ветвей топологически эквивалентно одной ветви, а «след» от их объединения остается в формуле эквивалентной функции. Это справедливо и для n последовательно соединенных ветвей.

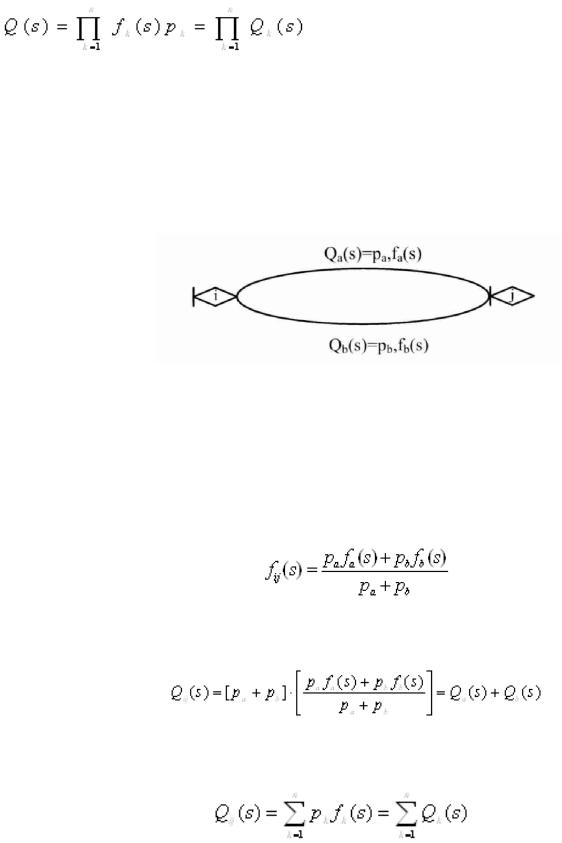
Несложно видеть, что стохастическая сеть, состоящая из n последовательно соединенных ветвей имеет эквивалентную функцию вида

13. Параллельное соединение ветвей стохастической сети

Рассмотрим стохастическую сеть (рис.3), состоящую из двух параллельных ветвей, характеризующихся вероятностями их выбора paи pb, а также преобразованиями Лапласа функций

плотности fa(s) и fb(s) вероятностей времен их реализации.

Рис. 3

Определим эквивалентную функцию Qij(s) этой стохастической сети.

По определению эквивалентной функции Qij(s) = pijfij(s).

При этом, pij = pa+pbи

.

Поэтому

.

Следовательно, если стохастическая сеть состоит из n параллельно соединенных ветвей, то

. (17)

Таким образом, эквивалентная функция стохастической сети, состоящей из параллельно

соединенных ветвей равна сумме эквивалентных функций этих ветвей.

14. Виды стохастических сетей и их типовые структуры. Простые стохастические сети

Простые стохастические сети.

Стохастическая сеть, состоящая из ветвей описывающих элементарные физические процессы и логических узлов (вершин) одного типа называется простой стохастической сетью.

Как следует из определения, данный вид сетей является достаточно широким.

Однако на практике наибольшее применение нашли сети, содержащие логические вероятностные вершины «Исключающее ИЛИ». Это обусловлено тем, что в этом случае стохастическая сеть точно совпадает с определением алгоритма, в котором ветви соответствуют операторам действия, а промежуточные вершины условным операторам.

Использование узлов других типов в простых стохастических сетях весьма ограниченно, так как моделирование реального случайного процесса при помощи только логического «И» или «Включающего ИЛИ» затруднительно и приводит, как правило, к сетям, содержащим одновременно несколько типов вершин и не соответствующим данному выше определению.

Очевидно, что целью моделирования процесса функционирования системы связи или ее элементов является получение аналитических выражений для вычисления значений показателей качества и эффективности. Это становится возможным только после определения эквивалентной функции, имеющей физический смысл вероятности реализации исследуемого процесса за время меньшее некоторого времени наступления катастрофы в системе. Под катастрофой понимается такое событие, что система перестает отвечать требованиям к качеству (эффективности) реализуемого ею целевого процесса. При этом поток наступления катастроф является пуассоновским (см. производящие и характеристические функции). Так как целевым процессом, при моделировании систем связи является процесс передачи (доставки) потоков сообщений, то катастрофой в этом случае является факт старения сообщений за время их передачи (доставки) по системе связи.

Понятно, что если сеть состоит из малого числа ветвей и в целом может быть преобразована к одной из базовых структур, то задача определения эквивалентной функции не вызывает никаких трудностей.

Однако на практике приходится иметь дело с сетями, сведение которых к базовым достаточно сложно. Примером такой сети является простая стохастическая сеть, содержащая множество контуров (составных петель). Для изучения сетей данного типа введем понятия замкнутой стохастической сети и пели k-го порядка.

Предварительно заметим, что петлей первого порядка принято называть петли, не содержащие других петель и позволяющие достичь каждый узел петли из любого другого.

Петлей k-го порядка называется множество k не связанных между собой петель первого порядка.

Эквивалентная функция петли k-го порядка определяется как

,

где Qi(s) – эквивалентная функция i-й петли первого порядка, определяемая как произведение эквивалентных функций ветвей, входящих в эту петлю.

Замкнутой стохастической сетью называется сеть, в которой каждая ветвь принадлежит, по крайней мере, одной петле.

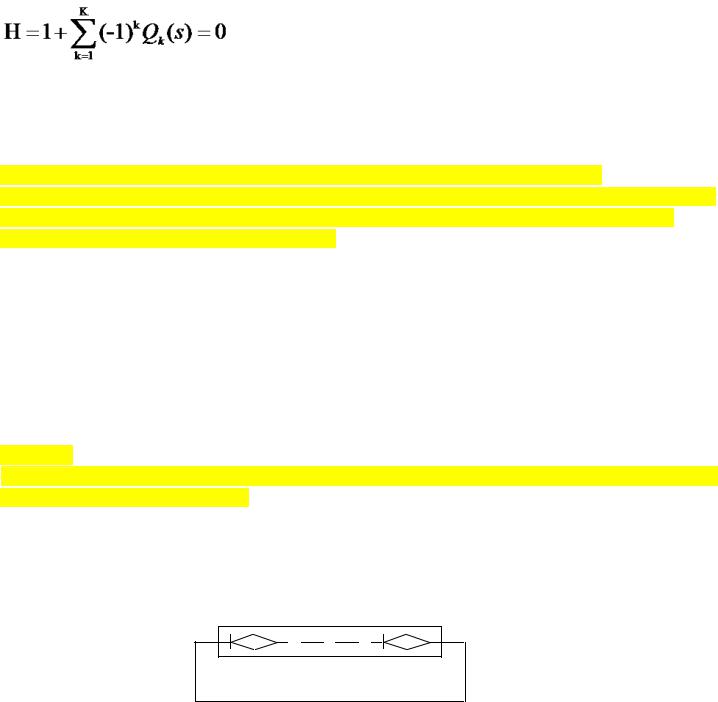
Определение эквивалентной функции стохастической сети, по сути, преобразует исходную сеть в замкнутую. Это позволяет использовать для определения эквивалентной функции исходной сети топологическое уравнение Мейсона для замкнутых графов

(19)

здесь K – максимальный порядок петель, входящих в стохастическую сеть.

Анализ уравнения показывает, что в него входит и эквивалентная функция исходной стохастической сети, как замыкающая ветвь, образующая петлю первого порядка.

Таким образом, если имеется простая стохастическая сеть, состоящая из параллельных, последовательных цепей и петель, то при помощи топологического уравнения и использования базовых структур она может быть преобразована в эквивалентную сеть, содержащую единственную ветвь, характеризуемую эквивалентной функцией сети.

15. Определение вероятностно – временных характеристик стохастической сети

Прежде чем перейти к рассмотрению способов определения вероятностно-временных характеристик представленного стохастической сетью случайного процесса, докажем существенное свойство эквивалентной функции.

Теорема 1

Стохастическая сеть, соответствующая стационарному случайному процессу имеет эквивалентную функцию, голоморфную при Re s >0.

Доказательство.

Рассмотрим стохастическую сеть произвольной структуры (рис.11).

Qэ(s)

Qa(s)

Рис. 11

На рис.11 Qэ(s) - эквивалентная функция стохастической сети; Qa(s)=1/Qэ(s) - дополнительная дуга, соединяющая сток j c источником i.

Функция Qэ(s) определяется из топологического уравнения Мейсона

где Wm(s) - эквивалентные функции петель m-го порядка, определяемые как произведение эквивалентных функций wi(s) m не связанных между собой петель первого порядка, то есть

m

Wm (s) wi (s) ;

i 1

n

wi (s) fi (s) ; -

j 1

- эквивалентная функция i-й петли первого порядка;

fi (s) e st fi (t)dt ,

0

- преобразование Лапласа функции плотности вероятностей времени свершения i-го элементарного процесса. Исходя из свойств преобразований Лапласа функция fi(s) является голоморфной.

С учетом (21), эквивалентная функция Qэ(s) для сети произвольной структуры имеет вид:

l 1

где k – количество функций fi(s) в прямой цепи стохастической сети; M – максимальный порядок петель данной стохастической сети.

Несложно видеть, что производная функции (22)

существует в окрестности каждого полюса s0 и не изменяет своего знака в области определения, а значит Qэ(s) является голоморфной. Теорема доказана.

Доказанное свойство голоморфности эквивалентной функции обусловливает правомочность следующих двух основных подходов к определению вероятностно-временных характеристик представленного стохастической сетью случайного процесса.

16. Метод двухмоментной аппроксимации [11, 13, 14]

Особенностями этого метода является:

1.Придание вероятностного смысла эквивалентной функции стохастической сети: Q(s) – вероятность того, что процесс передачи сообщений по системе связи будет завершен успешно до случайного момента времени старения этих сообщений.

2.Принятие ограничений на вид функции распределения времени старения передаваемой информации Z(t).

Вобщем случае, вероятность того, что случайное время передачи tП, распределенное по закону H(t), будет меньше случайного времени старения информации tc, распределенное по закону Z(t) равна

Таким образом, реальная функция распределения времени передачи была аппроксимирована неполной гамма - функцией, с параметрами, определяемыми из эквивалентной функции стохастической сети, что и дало название этому методу. Следует заметить, что если исследователю априорно известен закон распределения, наиболее полно характеризующий исследуемый процесс, то аналогичным образом можно выполнить аппроксимацию этим законом реальной функции распределения.

17.Метод обращения [14, 15]

Вотличии от первого, второй подход к определению вероятностно-временных характеристик систем связи не предусматривает ограничений на вид закона распределения времени старения передаваемой информации. Поэтому, эквивалентная функция стохастической сети рассматривается не как вероятность своевременной передачи, а как изображение исследуемого процесса доставки сообщений по Лапласу. Действительно, функция

является классическим представлением интегрального преобразования Лапласа функции–оригинала f(tП) - функции плотности вероятностей времени tП. В свою очередь, определение изображений подпроцессов исследуемого процесса передачи и сам алгоритм формирования эквивалентной функции является типичным для операционного исчисления методом, широко применяемым для исследования сложных функций. Что касается параметра s, то в данном случае он представляет собой не интенсивность старения передаваемой информации, а является комплексной переменной:

s = + jy, - < y < + .

Таким образом, интеграл (26) является преобразованием Лапласа, ставящим в соответствие каждой функции (оригиналу) f(tП), tП > 0, единственную функцию Q(s) (изображение) комплексной переменной, причем для существования изображений необходима сходимость этого интеграла. Отсюда вытекает первый важный шаг анализа – проверка сходимости интеграла Лапласа. Напомним, что признаком абсолютной и равномерной сходимости (26) является существование предела [4, 5]

и аналитичность функции Q(s), при Re(s) = 0 Точная нижняя грань a действительных чисел 0, для которых выполняется это условие называется абсциссой абсолютной сходимости преобразования Лапласа. При этом в полуплоскости Re(s) 0 изображение Q(s), определяемое из стохастической сети с использованием уравнения Мейсона, как было доказано выше, является голоморфной (однозначной аналитической) функцией. Областью определения функции Q(s) является полная s-плоскость, за исключением особых точек, расположенных слева от прямой = a.

Достаточными условиями существования обратного преобразования являются:

Если Q(s) аналитична для a и имеет порядок меньше –1, то обратное преобразование Лапласа L-

1[Q(s)] существует; оно непрерывно для всех t>0 и f(t) асимптотически сходится к функции exp[ at] при t с абсцисой абсолютной сходимости a, а при t 0 L-1[Q(s)] 0;

Если Q(s)= [Qi(s), i=1,n], при (si, i=1,n) аналитичной относительно каждого si, равна нулю при si=0, i=1,n и Qi(s) = L[fi(t)] ( ai,i=1,n), то L-1[Q(s)] существует и соответствующее преобразование Лапласа имеет абсциссу абсолютной сходимости.

Задача определения оригинала f(t), соответствующего эквивалентной функции стохастической сети Q(s) является достаточно сложной и для ее решения используются способ контурного интегрирования и методы разложения Q(s) (с целью упрощения ее вида), с последующим почленным переходом в пространство оригиналов.

Способ контурного интегрирования подразумевает полное определение функции Q(s) для всех значений комплексной переменной s = + jy, - < y < + , а поэтому его использование зачастую весьма трудоемко и на практике применяется достаточно редко.