Отчеты / ЛАБ8

2

1 Введение

Цель работы: изучение совместно применения устройства средней степени интеграции.

Задание:

1)Разработать обобщённую функциональную схему устройства;

2)Описать составные части схемы;

3)Составить таблицы функционирования операционного блока;

4)Организовать приём и выдачу данных согласно варианту, используя встроенные блоки регистров и счётчиков;

5)Создать схему реализации вычислительного блока, выполняющего заданные операции и осуществляющего приём входных данных и выдачу результата согласно варианту;

6)Составить план моделирования в виде двух столбцов таблицы: входные данные, выходные данные. Использовать для каждой операции по два различных набора данных;

7)Промоделировать работу схемы в двух режимах. Провести анализ результатов моделирования разных режимов;

8)Сверить результаты моделирования с составленными таблицами истинности;

9)Повторить п. 4 – 8, только для описания устройств вместо схем на холстах .bdf используйте заданный вариантом HDL;

10) Написать выводы о проделанной работе.

Задание по варианту:

1)Прием: Е – , L P, R s;

2)Выдача: E +, U L, RD 1;

3)Операции: задача 8, OP1 ∩ , OP2 A+B;

4)HDL: SystemVerilog.

3

2 Ход работы

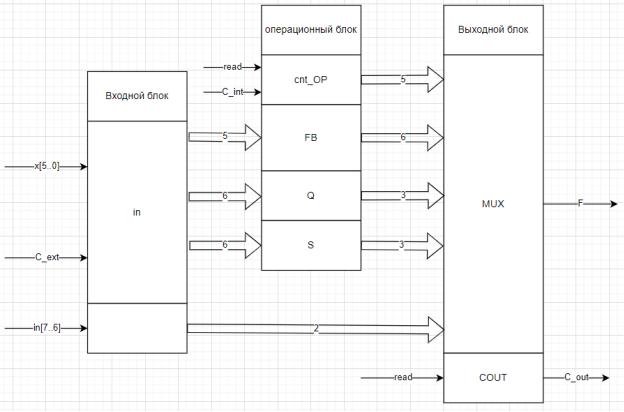
Была построена функциональная схема. На рисунке 1 представлена схема.

Рисунок 1 – Функциональная схема.

Также были построены таблицы истинности для 3 операций.

При вводе кода «01» согласно варианту выполняется задача №8 – «Разработать схему декодирования Commodore GCR-кода в двоичное число. При несовпадении входного символа с таблицей установить выход FB=1».

Таблица истинности для задачи представлена ниже.

4

Таблица 1 – Таблица истинности для задачи №8

При вводе кода «10» согласно варианту выполняется операция конъюнкции слов А и инверсного В. Таблица истинности для данной задачи представлена ниже.

Таблица 2 – Таблица истинности для конъюнкции.

5

При вводе кода «11» согласно варианту выполняется операция сложения слов А и В. Таблица истинности для данной задачи представлена ниже.

Таблица 3 – Таблица истинности для суммы.

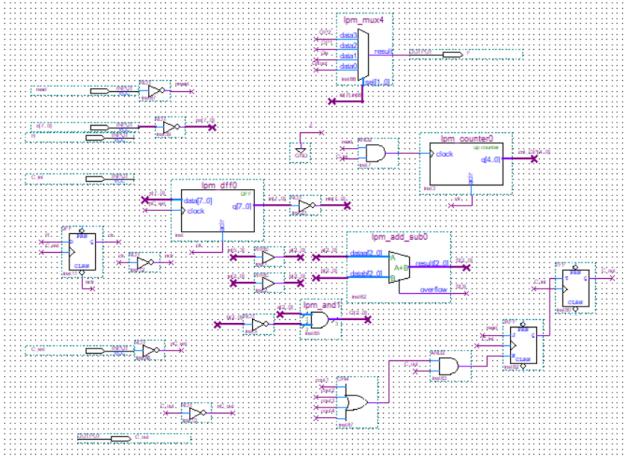
Также была построена схема. Схема представлена на рисунках 2 – 4.

Рисунок 2 –Первая часть схемы.

6

Рисунок 3 – Вторая часть схемы.

Рисунок 4 – Третья часть схемы.

Ниже в таблице 4 представлен план моделирования.

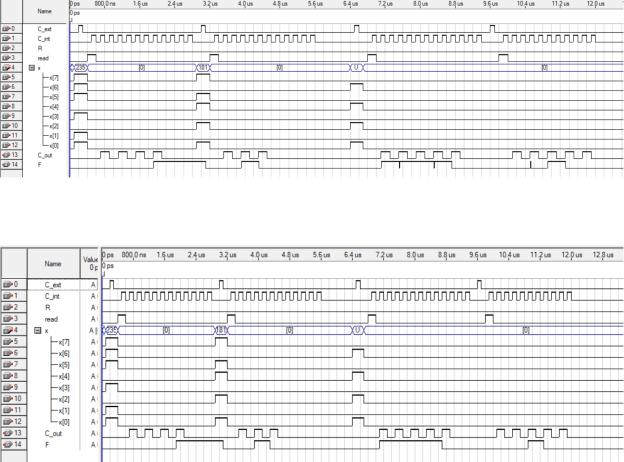
После построения схемы было проведено моделирование в двух режимах timing и functional. Результаты моделирования представлены на рисунках 5 и 6.

На первом временном промежутке 0 – 2100нс изображён результат выполнения операции 11 (сигнал 6). Было произведено сложение сигналов 101 + 011. Результатом данной суммы является 1000, что и изображено на моделировании.

На втором временном промежутке 2900 – 4500нс показан результат выполнения операции 10 (сигнал 4). Была произведена функция 110 ∩ 101 .

Результатом функции является сигнал 010. Результат сходится с моделированием.

На третьем временном промежутке 6400 – 8900нс изображён результат выполнения операции 01 (сигнал 2). Были поданы следующие входные данные: x4 =1, x3 =0, x2 =1, x1 =0, x0 =1. Из таблицы 1 сигнал FB при этих

8

входных данных должен принимать значение 1. Результат сходится с моделированием

На четвёртом временном промежутке 9800 – 11900нс показан результат операции 00. На данном промежутке выводиться количество проделанных операций. На моделировании выведено 5 проделанных операций (4 операции с входными данными и 5-ая операция была засчитана как операция с счётчиком).

Рисунок 5 - Результат моделирования в режиме timing.

Рисунок 6 – Результат моделирования в режиме functional.

Для данного вычислительного блока был написан код на System Verilog. Весь код написан ниже:

module Finalsv (

input logic C_int, C_ext, RD, R,

9

input logic [7:0] x, output logic F,C_out );

logic [3:0] y,S; logic [2:0] Q; logic [4:0] cntOP; logic [7:0] in; logic FB;

reg [3:0] state;

assign nC_ext = ~C_ext; always_ff @(posedge nC_ext) if (R)

in[7:0] <= 8'b0; else in <= x;

always_ff @(posedge C_int) begin

{S[3],S[2:0]} <= in[5:3] + in[2:0]; Q[2:0] <= in[5:3] & ~in[2:0];

if (R) begin S <=4'b0; Q <= 3'b0;

F<= 1'b0;

10

end

else case (state) 0: begin

if (RD) state <= 1; C_out <= 1'b0; end

1: begin C_out <= 1'b1;

if (~in[7] & ~in[6]) F<= cntOP[0]; else if (~in[7] & in[6]) F <= y[0]; else if (in[7] & ~in[6])

F<=Q[0];

else F <= S[0]; state <=2; end

2:begin C_out <= 1'b0; state <=3;

end

3:begin C_out <= 1'b1; if (~in[7] & ~in[6]) F<= cntOP[1];

else if (~in[7] & in[6])