3. Алгоритм аппроксимации функции методом наименьших квадратов

Схема алгоритма, аппроксимации функции по методу наименьших квадратов (МНК) приведена на рис. 2.4-1.

МНК[3] является одним из наиболее распространенных методов аппроксимации функции. В этом методе параметры a₀, a₁, ..., a_n определяются из условия минимума суммы квадратов отклонений значений аппроксимирующей функции от табличных данных.

Вектор коэффициентов a^T определяют из условия минимизации

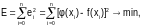
где (n+1) – количество узловых точек.

φ(x)=a₀φ₀(x)+a₁φ₁(x)+...+a_mφ_m(x) – аппроксимирующая функция степениm

Для получения искомых значений параметров a₀, a₁,…a_mследует составить и решить систему (m+1) линейных уравнений

В качестве меры уклонения заданных значений функции y₀, y₁, ..., y_n от многочлена степени m -, принимается величина

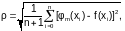
Поскольку МНК требует решения системы линейных уравнений (СЛУ), на рис. 2.4-2 приведена схема алгоритма решения СЛУ методом Гаусса [1]. Метод сводится к последовательному исключению из всех уравнений, начиная со второго, затем - начиная с третьего и т.д. Это позволяет получить эквивалентную систему, имеющую треугольную матрицу (прямой ход), а затем, действуя в противоположной последовательности, получают решение (обратный ход).

Рис. 2.3-1.Алгоритм метода наименьших квадратов

Рис. 2.3-2. Формирование матрицы Грама

Рис. 2.3-3. Вычисление элемента матрицы Грама

Рис. 2.3-4. Вычисление элемента правой части системы нормальных уравнений

Рис. 2.3-5.Решение системы линейных уравнений методом Гаусса

Рис. 2.3-6.Вычисление значения аппроксимирующей функции в заданных точках

Рис. 2.3-7. Вычисление невязки

4. Алгоритмы методов численного интегрирования

В основу всех методов численного интегрирования положена замена подынтегральной функцию f(x) приближенной функцией, которая может быть проинтегрирована в аналитическим виде. В качестве такой функции обычно используют полином Р_n(х) с узлами интерполяции в точках х₀, х₁, …,х_n. Для получения простых формул на элементарных отрезках интегрирования используют полиномы нулевой, первой и второй степени и соответственно получают формулы численного интегрирования: прямоугольников, трапеций и Симпсона.

Во всех алгоритмах оценка погрешности проводится с использованием метода двойного просчета [3], который основан на двукратном вычислении значения интеграла вначале с шагом h(где h=(b-a)/n), а затем с шагом h/2. Значения интегралов I_hи I_h/2 могут быть применены для оценки погрешности интегрирования по формуле Рунге:

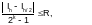
где: k - порядок точности метода.

1. Метод средних прямоугольников

Схема алгоритма процедуры для вычисления определенного интеграла методом средних прямоугольников представлена на рис. 2.4-1. Эта схема требует дополнения процедуры-функции f(x), в которой вычисляется значение подынтегральной функции.

Алгоритм метода основан на замене подынтегральной функции f(x) в пределах элементарного отрезка [x_i;x_i+1] интерполяционным многочленом нулевой степени, равным значению функции в середине отрезка [3]. Вычисление интеграла проводится с использованием формулы:

Оценка погрешности проводится с использованием метода двойного просчета, где в формуле Рунге k=2.

Рис. 2.4-1. Метод средних прямоугольников