2. Алгоритмы численных методов

   1. Алгоритмы методов решения нелинейных уравнений

      1. Метод половинного деления

Решение нелинейного уравнения методом половинного деления с использованием процедуры, схема алгоритма которой представлена на рис. 2.1-1, требует дополнения процедуры-функции f(x), в которой вычисляется левая часть уравнения. Корень уравнения f(x)=0 должен быть предварительно отделен на отрезке [a;b].

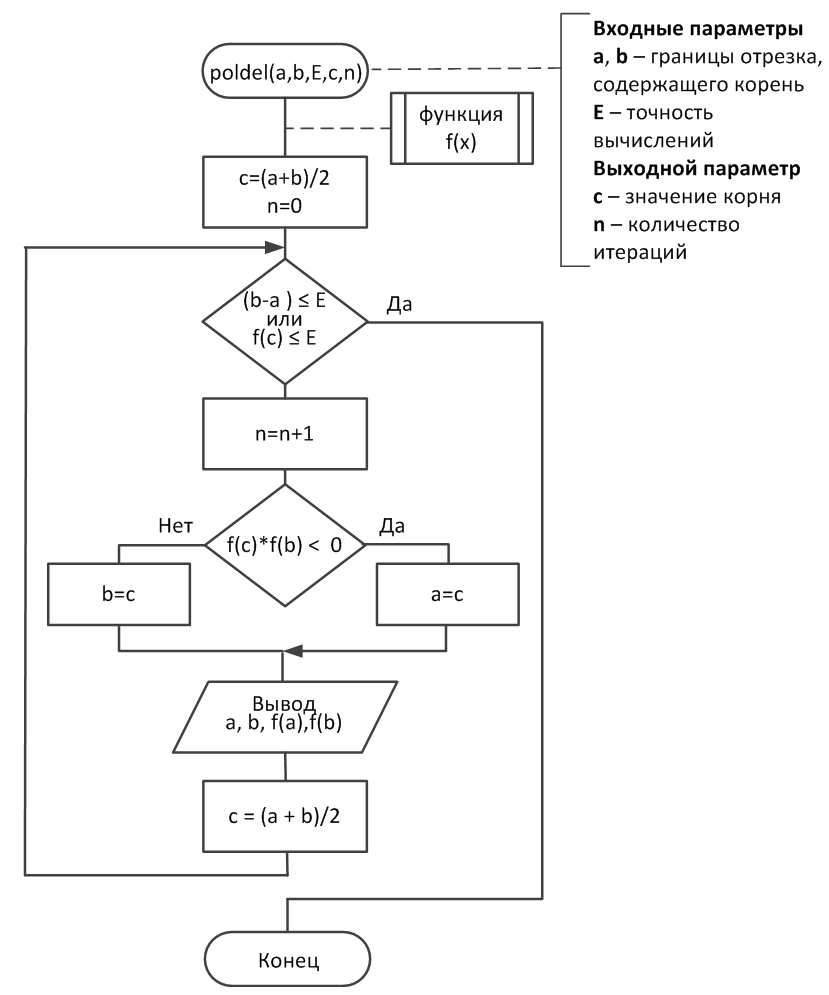
Рис. 2.1-1. Алгоритм метода половинного деления

Суть метода половинного деления [3]заключается в получении последовательности вложенных друг в друга отрезков [a₁;b₁], [a₂;b₂], …,[a_i;b_i],…, [a_n;b_n], таких что f(a_i).f(b_i) <0, где i=1,2,…,n. При этом длина каждого последующего отрезка вдвое меньше длины предыдущего. Тогда последовательное сужение отрезка вокруг неизвестного значения корня ξнанекотором шаге nобеспечивает выполнение неравенства |b_n - a_n|<e, которое и является условием выхода из цикла.Очевидно, что с точностью любое может быть принято за приближенное значение корня. Обычно выбирают середину отрезка

2. Метод итераций

Алгоритм процедуры, реализующей решение нелинейного уравнения методом итераций, представлен на рис. 2.1-2. Его использование требует дополнения двух процедур-функций: fi(x)–итерирующая функция и f(x)– левая часть исходного уравнения.

Рис.2.1-3. Алгоритм метода итераций

Метод итераций предполагает замену уравнения f(x)=0 равносильным уравнением x=j(x) [3].Функция j(x) называется итерирующей функцией. Если корень уравнения отделен на отрезке [a;b], то исходя из начального приближения x₀Î[a;b], получают последовательность приближений к корню:

x₁ = j(x₀), x₂ = j(x₁), …, x_n= j(x_n-1).

Условие сходимости метода итераций определяется теоремой:

Если все члены последовательности x_n=j(x_n-1)Î [a;b]и существует такое q (0<q<1), что для всех хÎ [a; b] выполняется условие |j’(x)| = q<1,то эта последовательность является сходящейся, а процесс итерации сходится к корню уравнения независимо от выбора начального приближения.

3. Метод Ньютона

Алгоритм процедуры, реализующей решение нелинейного уравнения методом Ньютона, представлен на рис. 2.1-3. Корень нелинейного уравнения должен быть отделен на отрезке [a;b], причем первая и вторая производные ( и ) непрерывны и знакопостоянны при хÎ [a;b].

Использование алгоритма требует двух процедур-функций: f(x)–левая часть исходного уравнения и f1(x)– производная от f(x).

Все последующие приближения к корню получаются с использованием итерационной формулы [3]

где i = 0, 1, …n-1.

В качестве начального приближения к корню выбирают точку х₀Î[a;b], где .

Процесс вычислений прекращается, если

,

где ε - заданная точность;

- наименьшее значение при

- наибольшее значение при

Для оценки полгрешности также используются следующих выражений:

Рис.2.1-3. Алгоритм метода Ньютона

4. Метод хорд

Схема алгоритма процедуры, реализующей метод хорд, представленная на рис. 2.1.4.-1, требует дополнения процедуры-функции f(x), в которой вычисляется левая часть уравнения.

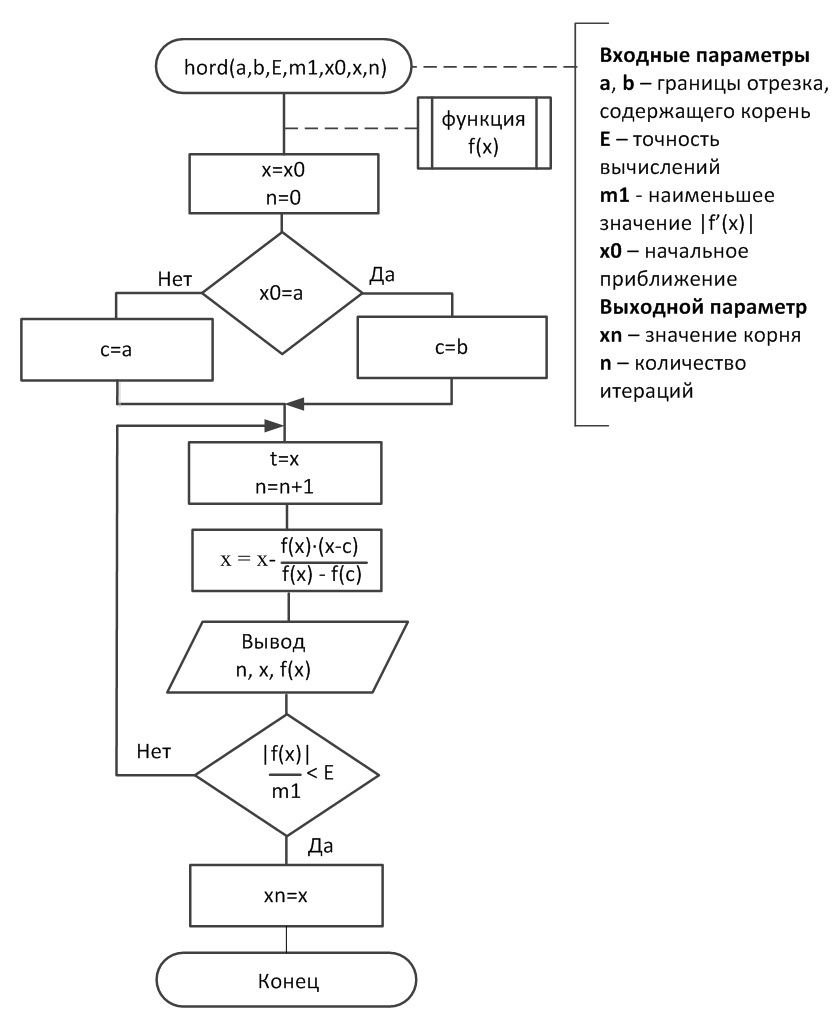
Рис.2.1-4. Алгоритм метода хорд

Корень нелинейного уравнения должен быть отделен на отрезке [a;b], причем первая и вторая производные ( и ) непрерывны и знакопостоянны при хÎ [a;b].

Рекурентная формула метода хорд [3]:

где - неподвижная точка.

Неподвижен тот конец отрезка [a;b], для которого знак функции f(x) совпадает со знаком ее второй производной. Тогда второй конец отрезка можно принять за начальное приближение к корню, то есть точку х₀.

Оценка погрешности метода хорд можно определить одним из выражениями:

где m₁и M₁ – соответственно, наименьшее и наибольшее значения при .

В случае, если M₁<2m₁, то для оценки погрешности метода может быть использована формула

| x_n-x_n-1|£e.