Учебники 80361

где величины с индексами х, у, z обозначают составляющие векторов поля по координатным осям.

В цилиндрической системе координат (рис.4) дивергенция и ротор выражается соотношениями

Рис.4

23

На основании (1.13)÷(1.16), (1.27) и (1.28) уравнения Максвелла в цилиндрической системе координат можно представить следующим образом:

составляющие векторов поля по осям (рис.4).

Скалярная форма уравнений Максвелла на практике используется также и в сферической системе координат.

1.2.5.Материальные уравнения среды

Ни в одной из рассмотренных выше форм уравнения Максвелла не образуют полной замкнутой системы, позволяющей рассчитывать электромагнитные процессы при наличии материальной среды. Поэтому их дополняют

соотношениями, связывающими векторы E , H , Д , B и пр ,

24

которые не являются независимыми. Связь между этими векторами определяется свойствами среды и ее состоянием,

Соотношения (1.37) принято называть материальными уравнениями, или уравнениями состояния среды, поскольку они описывают ее электромагнитные свойства, которые

В зависимости от свойств этих параметров различают линейные и нелинейные среды. Линейные среды, в свою очередь, делятся на однородные и неоднородные, изотропные и анизотропные.

Линейными называют среды, свойства которых не зависят от величины поля. Среды, параметры которых a , a

и б являются функциями напряженностей электрического и магнитного полей, будут нелинейными. К однородным относятся среды, обладающие одинаковыми свойствами во всех точках. Если значения электродинамических параметров (хотя бы одного из них) зависят от координат точки наблюдения, то среда считается неоднородной. Изотропной называется среда, свойства которой не зависят от направления

векторов E и H . В противном случае среда будет анизотропной [1]. Обычно анизотропия проявляется либо для электрического, либо для магнитного поля. Так например, кварц анизотропен к электрическому полю, а ферриты – к магнитному.

Уравнения состояния в общем случае очень сложны,

так как векторы Д , B , и пр в данной точке пространства в

данный момент времени могут зависеть от E и H во всех точках среды во все предшествующие моменты времени. В некоторых средах (сегнетоэлектрики и ферромагнетики)

25

векторы Д и B могут быть отличными от нуля при E =0 и

H =0.

Однако для большинства изотропных сред, вплоть до весьма значительных полей, материальные уравнения имеют простую линейную форму

где ст – плотность так называемых сторонних токов, т.е.

токов, поддерживаемых любыми силами, кроме сил электрического поля (например, магнитным полем, диффузией и т.д.). К сторонним, в частности, относят токи в передающих антеннах, считая при этом, что они не зависят от возбуждаемого ими электромагнитного поля.

В случае анизотропной среды зависимость между Д и

E будет иметь по форме такой же вид, что и для изотропной среды:

azx azy azz

Векторное уравнение (1.39) можно представить в виде трех скалярных уравнений:

Дx axx Ex axy Ey 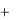axz Ez ,

Дy ayx Ex ayy Ey ayz Ez ,

Дz azx Ex azy Ey azz Ez ,

из которых следует, что каждая составляющая вектора Д

зависит от всех составляющих вектора E , в связи с чем между

Д и E может нарушаться коллинеарность.

Соотношения, аналогичные приведенным для Д ,

могут быть записаны и для B .

26

Уравнения Максвелла в скалярной форме (1.19)÷(1.26) и (1.29)÷(1.36) в случае линейной изотропной среды приводятся к виду:

а) в прямоугольной системе координат: