Учебники 80361

1.2.Описание электромагнитных полей с помощью уравнений Максвелла

1.2.1.Общая характеристика уравнений

В своей работе ''Трактат об электричестве и магнетизме'', изданной в 1873 году, Джеймс Клерк Максвелл обобщил теоретические и экспериментальные исследования, проведенные такими учеными как Ом, Кулон, Лаплас, Ампер, Ленц, Фарадей и др., и показал, что самые разнообразные электромагнитные явления могут быть описаны с точки зрения теории поля небольшим числом уравнений, которые и принято называть уравнениями Максвелла. Эти уравнения относят к фундаментальным аналитическим соотношениям классической макроскопической электродинамики, поскольку они описывают электромагнитные процессы в произвольной среде.

Уравнения Максвелла связывают величины, характеризующие электромагнитное поле, с его источниками, т.е. с распределением в пространстве электрических зарядов и токов.

Уравнения Максвелла позволяют определить основные

характеристики поля ( E, H, Д и B ) в каждой точке среды в любой момент времени, если известны источники поля 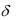и

как функции координат и времени (здесь - плотность токов, а - объемная плотность зарядов).

Современная форма записи уравнений Максвелла дана немецким физиком Г.Герцем и английским физиком О.Хевисайдом. Уравнения Максвелла записывают в интегральной, дифференциальной, скалярной и других формах.

1.2.2.Интегральная форма

Уравнения Максвелла в интегральной форме определяют по

заданным зарядам и токам не сами векторы поля E , H , Д , B

13

в отдельных точках пространства, а некоторые интегральные величины, зависящие от распределения этих характеристик

поля: циркуляцию векторов E и H вдоль произвольных

замкнутых контуров и потоки векторов B и Д через

произвольные замкнутые поверхности. Указанное обстоятельство является недостатком уравнений.

Первое уравнение Максвелла представляет собой обобщение на переменные поля эмпирического закона Ампера о возбуждении магнитного поля электрическими токами. Максвелл высказал гипотезу о том, что магнитное поле порождается не только токами в проводниках, но и переменными электрическими полями в диэлектриках или вакууме. Величина, пропорциональная скорости изменения электрического поля во времени, была названа Максвеллом током смещения, который возбуждает магнитное поле по тому же закону, что и ток проводимости (это подтвердилось при экспериментальной проверке).

Полный ток, равный сумме тока проводимости и тока смещения, всегда является замкнутым.

Первое уравнение Максвелла записывается в виде

H в каждой точке контура на бесконечно малый отрезок dl контура) определяется полным током iп через произвольную

поверхность S , ограниченную данным контуром. В (1.4) приняты следующие обозначения:

l - замкнутый контур интегрирования, сцепленный с

направленный к ней по нормали;

14

Д - вектор электрического смещения;

t – время.

Соотношение (1.4) называют также уравнением Максвелла-Ампера. В простейшем случае оно принимает вид

l

и известно в электротехнике под названием закона полного тока. Здесь w –число контуров (витков); i –контурный ток. При i=0 возникает неопределенность, т.к. возможны два случая:

1)контур l токи вообще не пронизывают;

2)токи пронизывают контур, но их сумма равна нулю. Это также является недостатком уравнений (1.4) и (1.5)

Второе уравнение Максвелла представляет собой математическую формулировку закона электромагнитной индукции Фарадея и записывается как

BdS

т.е. циркуляция вектора напряженности электрического поля

E вдоль замкнутого контура l (ЭДС индукции) определяется скоростью изменения потока вектора магнитной индукции через поверхность S, ограниченную данным контуром.

Уравнение (1.6) может быть получено из соотношений

где е – ЭДС индукции; Ф - магнитный поток, сцепленный с контуром l .

Второе равенство из (1.7) до Максвелла считалось справедливым только для проводящего контура. Максвелл предположил, что оно справедливо и для случая, когда среда не обладает проводимостью. Физически это означает, что любое изменение во времени магнитного поля приводит (не-

15

зависимо от свойств среды) к возникновению электрического поля.

Третье уравнение Максвелла, обычно называемое теоремой Гаусса, представляет собой обобщение закона взаимодействия неподвижных электрических зарядов – закона Кулона:

т.е. поток вектора электрической индукции Д через произвольную замкнутую поверхность S определяется электрическим зарядом Q, находящимся внутри этой поверхности (в объеме V, ограниченном данной поверхностью).

Формула (1.8) часто используется при расчетах электростатических полей. Максвелл показал, что еѐ можно применять и для расчета полей, изменяющихся во времени.

Четвертое уравнение Максвелла выражает опытные данные об отсутствии магнитных зарядов, аналогичных электрическим (магнитное поле порождается только токами):

S

т.е. поток вектора магнитной индукции B через произвольную замкнутую поверхность S равен нулю.

В (1.9) Ф=0 потому, что число входящих внутрь поверхности S и выходящих из нее магнитных силовых линий будет одинаковым, поскольку они всегда являются замкнутыми. Так как входящие линии считаются отрицательными, а выходящие положительными, то их сумма равна нулю.

1.2.3. Дифференциальная форма

Считая векторы E , H , Д , B непрерывными функциями

координат и рассматривая циркуляцию E и H по бесконечно малым контурам и потоки векторов Д и B через

16

поверхности, ограничивающие бесконечно малые объемы, можно от интегральных соотношений (1.4), (1.6), (1.8)и (1.9) перейти к системе дифференциальных уравнений, справедливых в каждой точке пространства и более удобных для решения различных задач.

Переход от интегральной формы уравнений к дифференциальной можно осуществить с помощью дифференциальных операций векторного анализа: дивергенции и ротора.

Дивергенцией (или расхождением) какого-либо вектора

A принято называть предел отношения его потока через замкнутую поверхность S к объему V, ограниченному этой поверхностью, при условии, что поверхность и объем стягиваются в точку, для которой определяется дивергенция.

В этом случае к нулю будут стремиться S и V. Математически

дивергенция вектора A выражается соотношением

площади S, ограниченной контуром l, при условии, что площадь S и контур l стягиваются в точку, для которой определяется ротор. Сказанное аналитически выражается формулой

S 0 S

В отличие от дивергенции ротор будет векторной величиной.

17

Из (1.4) с учетом (1.11) получим

Так как rotn H n , то можно положить равными и сами векторы, т.е.

rotH

или

Это и есть первое уравнение Максвелла в дифференциальной форме.

Совершенно аналогичным путем получают и второе уравнение Максвелла:

Из (1.8) с учетом (1.10) имеем

18

Здесь также объем V стягивается в точку, для которой определяется дивергенция. Поэтому

Из (1.16) следует, что поле вектора B не имеет истоков. Иначе говоря, магнитные силовые линии всегда замкнуты и не имеют ни начала, ни конца.

1.2.4. Скалярная форма

На практике при решении различных вопросов уравнения электромагнитного поля часто используют в скалярной форме. Они представляют собой зависимости между составляющими векторов поля по различным координатным осям. Вид этих соотношений существенно зависит от системы координат.

Сначала в прямоугольной системе координат выразим ротор и дивергенцию. Выбираем замкнутый контур интегрирования в плоскости ZOУ (рис.2) и вычисляем интеграл (направление обхода контура указано стрелкой)

где S 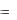y z ; Hx , H y , Hz - составляющие H по координатным

осям.

Следовательно,

19

Рис.2

20

Вычислим поток вектора Е через грани, параллельные плоскости УОZ:

считаются отрицательными, а выходящие - положительными. Различие в количестве силовых линий, входящих и

выходящих через параллельные грани, может быть обусловлено двумя причинами:

1)наличием в объеме V электрических зарядов;2)тем, что силовые линии могут входить и выходить не только через параллельные, но и через взаимно перпендикулярные грани (на рис.3 не показано).

Рис.3

21

Через грани, параллельные плоскостям ХОZ и УОХ, потоки будут равны.

Полный поток вектора Е определяется уравнением

на основании которого находим дивергенцию

Аналогично (1.17)и (1.18) выражают ротор и дивергенцию и для других векторов электромагнитного поля, в связи с чем уравнения Максвелла в скалярной форме для прямоугольной системы координат примут вид

22