Теория автоматического управления. лабораторный практикум. Харченко А.П

Таблица 10

Варианты изменений параметров в Nii число раз K°ii =K*Nii

71

Продолжение табл. 10

Nпос – для последовательного соеденения;

Nпар – для параллельного соединения;

Nвсп – для встречно-параллельного соединения.

72

ЛАБОРАТОРНАЯ РАБОТА № 4

ИССЛЕДОВАНИЕ ТОЧНОСТИ САР СКОРОСТИ

Цель работы: исследование точности статической и астатической системы автоматического регулирования скорости с пропорциональным и интегральным регулятором при различных типовых входных сигналах

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

При проектировании любой системы автоматического управления (САУ) к ней предъявляются, наряду с такими требованиями к качеству регулирования как время регулиро-

вания и перерегулирование, требования к точности воспро-

изведения задающего (входного) воздействия (сигнала). Точность в теории управления оценивается величиной

обратной ошибкой ε.

Технические системы, в зависимости от наличия составляющих ошибки, подразделяются на статические или астатические (системы с астатизмом первого, второго порядков). Рассмотрим показатели качества, характеризующие вынужденную (установившуюся) составляющую ув(t), по которой определяют точность системы. Если входная величина системы - сигнал х(t), то установившаяся ошибка регулирования системы определяется: εв(t)= х(t) - ув(t), где ув(t) вынужденная составляющая регулируемой величины.

При любом плавном входном сигнале ошибка автоматической системы определяется

ε (t) = Со *х(t) + C1 *d х(t) / dt + C2 / 2 *d² х(t) / d²t,

где Со – коэффициент позиционной ошибки; С1 – коэффициент скоростной ошибки; С2 – коэффициент ошибки по ускорению; х(t) – закон изменения входного сигнала.

73

В зависимости от закона изменения входного сигнала

х(t) (единичная ступенчатая функция, линейная функция и нелинейная функция), можно исследовать только позиционную, позиционную и скоростную или все три составляющие ошибки.

Введение в структурную схему различных типов регуляторов скорости делают систему статической или астатической, уменьшая составляющие ошибки. В статических системах присутствуют все составляющие ошибки, в астатических системах с астатизмом первого порядка отсутствует позиционная ошибка. САР скорости с пропорциональным регулятором – статическая система, а САР скорости с интегральным регулятором - система с астатизмом 1-го порядка.

Коэффициенты ошибок Со, С1, С3 определяются из структурной схемы системы.

В статических системах коэффициент Со отличен от нуля. В системах с астатизмом первого порядка Со =0, С1 не равно нулю. В системах с астатизмом второго порядка Со =С1= 0, С2 не равно нулю.Увеличение числа интегрирующих звеньев приводит к повышению порядка астатизма системы, т. е. к нулевым значениям нескольких коэффициентов ошибок, но при этом усложняется обеспечение устойчивости системы.

Если на систему помимо задающего воздействия Х(р) действует и возмущение F(p), то астатизм системы относительно F(p) зависит от места включения интегрирующего звена.

Коэффициент позиционной или статической ошибки САР скорости определяется:

Со = | Wо(p) | p=0 = 1 / (1 + Крс*Ксу*Кд*Кдс),

где Крс – коэффициент передачи регулятора скорости РС; Ксу

– коэффициент передачи системы управления СУ; Кд – коэффициент передачи двигателя Д; Кдс – коэффициент передачи датчика скорости ДС.

74

Скоростная составляющая ошибки определяется как производная от ММ (передаточной функции) САР скорости по аргументу “p”. Скоростная составляющая для САР скорости определяется:

С1 = | d Wо(p)/dt | p=0 = 1 / (Крс*Ксу*Кд*Кдс).

При входном сигнале ступенчатая единичная функция, можно наблюдать в САР скорости позиционную ошибку, а при линейном позиционную и скоростную или скоростную.

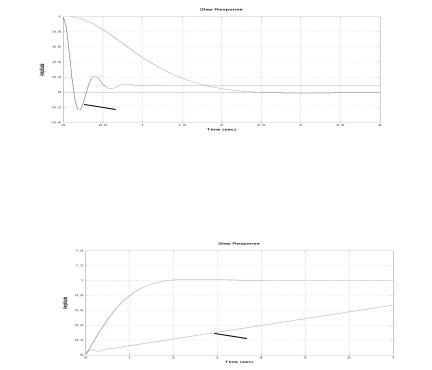
На рис. 29 представлены переходные процессы САР скорости по позиционной ошибке при единичном ступенчатом входном сигнале: 1- с П-регулятором; 2 – с И – регулятором.

2

1

Рис. 29. Переходные процессы САР скорости по ошибке при единичном ступенчатом входном сигнале

На рис. 30 представлены переходные процессы САР скорости по ошибке при линейном входном сигнале: 1- с П- регулятором; 2 – с И – регулятором.

2

1

Рис. 30. Переходные процессы САР скорости по ошибке при линейном входном сигнале.

75

Для статической и астатической автоматической системы можно представить графики зависимости установившейся позиционной ошибки εуст1 при входном сигнале единичная ступенчатая функция и установившейся скоростной ошибки εуст2 при входном сигнале линейная функция от коэффициента передачи регулятора Крег.

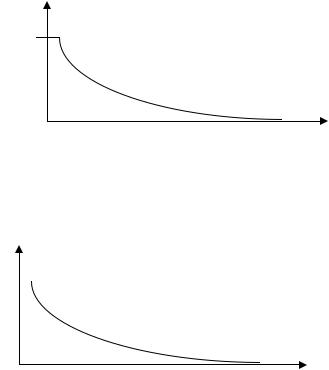
Для статической системы зависимость установившееся значения позиционной ошибки εуст1=1/(1+Краз) при изменении Крег от 0 до ∞ и входном сигнале x(t)=1(t ) представлена на рис. 31.

εуст1

1

Крег

Рис. 31. Зависимость позиционной ошибки

Для астатической системы зависимость установившееся значения скоростной ошибки εуст2=1/Краз при изменении Крег от 0 до ∞ представлена на рис. 32.

εуст2

Крег

Рис. 32. Зависимость скоростной ошибки

76

В качестве регулятора скорости в среде МАТЛАБ используется параллельное соединение П-звена, И-звена и Д-звена, которое реализуется в блоке ПИД - контроллера.

Передаточная функция ПИД - контроллера

Wпид = К1 + К2/р + К3*р,

где К1,К2 и К3 – коэффициенты передачи пропорционального, интегрирующего и дифференцирующего типовых звеньев.

Переходная характеристика ПИДконтроллера

h(t) = К1*1(t) + К2*t + К3*d1(t)/dt.

Импульсная переходная характеристика ПИД - контрол-

лера

dh(t)/dt = К1*d1(t)/dt + К2 + К3*d δ(t) /dt.

Различные комбинации задания коэффициентов К1,К2 и К3 определяют составляющие временных характеристик.

П - регулятор это статический регулятор, который формирует пропорциональный закон регулирования.

При увеличении статического К1 уменьшается установившаяся ошибка, но усиливаются шумы измерения, что приводит к повышению активности исполнительных элементов (работают рывками), механическая часть изнашивается и существенно уменьшается срок службы оборудования.

Для П- регулятора в статической системе существуют недостатки:

неизбежное отклонение регулируемой величины от заданного значения, если объект статический;

замедленная реакция регулятора на возмущающие воздействия в начале переходного процесса.

77

И - регулятор это интегральный регулятор, который существенно улучшает точность регулирования в статике:

установившаяся позиционная ошибка при постоянном входном воздействии равна нулю;

ошибка нечувствительна к изменениям параметров системы.

Для И- регулятора в статической системе существуют недостатки:

повышается астатизм системы на единицу и, как следствие, снижение запасов устойчивости;

увеличивается колебательность переходного процесса, увеличивается инерционность.

При использовании в автоматической системе ПИДрегулятора на низких частотах преобладает интегрирующий эффект, а на высоких – дифференцирующий.

Статическая система при установке ПИД-регулятора становится астатической (статическая ошибка равна нулю), однако в переходном процессе астатизм снимается за счет действия дифференцирующей составляющей, т. е. качество переходного процесса улучшается.

Пропорциональная часть регулятора К1 эффективно повышает быстродействие управления с одновременным увеличением колебательности, а также уменьшает установившуюся ошибку.

Интегральная составляющая регулятора К2 устраняет установившуюся ошибку (обеспечивается астатизм), но, как правило, несколько затягивает переходный процесс.

Дифференциальная составляющая регулятора К3 увеличивает запас устойчивости системы и, как следствие, возможно увеличение коэффициента усиления для повышения точности, уменьшает перерегулирование и повышает быстродействие в замкнутой системе.

78

ПРЕДВАРИТЕЛЬНОЕ ЗАДАНИЕ

Предварительным заданием при исследовании точности системы автоматического регулирования скорости являются математические модели элементов САР скорости, используемые в лабораторной работе №3.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ ЛАБОРАТОРНОЙ РАБОТЫ

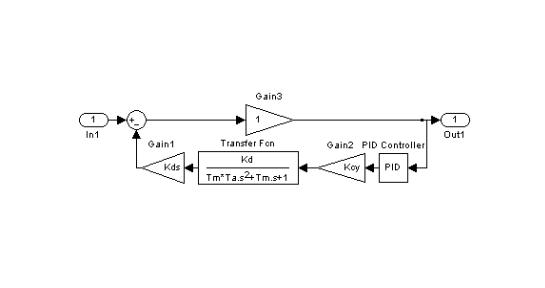
1. Задать схему моделирования САР скорости для выходного сигнала ошибки, представленную на рис. 33.

Рис. 33. Схема моделирования ошибки САР скорости 2. Исследование ошибки САР скорости с пропорцио-

нальным регулятором и ступенчатым входным сигналом.

2.1. Для задания единичного входного сигнала х(t)=К1*1(t)

задать параметры PID контроллера следующими:

Proportional: К1 Integral: 0 Derivat: 0.

2.2. Задать параметры схемы: звено РС – PID - контроллер пропорциональное (Крег=К1), звено СУ – пропорциональное (К=Ксу), звено ДПТ – типовое звено 2-го порядка (К=Kd2 Тм=Тm2, Tэ=Ta2) и звено ДС – пропоциональное (Кдс=Кds).

79

2.3.Получить переходную характеристику по ошибке, задав последовательность команд (см. л.р. 3).

2.4.По переходной характеристике измерить установившееся значение переходной характеристики hуст = εуст1 .

2.5.Задавая несколько значений Крс (не менее 5) повторить п.п. 3.2.2-3.2.3 получить переходные характеристики.

2.6.Построить график зависимости εуст1=F(Крег).

3.Исследование ошибки САР скорости с пропорцио-

нальным регулятором и линейным входным сигналом.

3.1.Задать на входе схемы ннтегрирующее звено.

3.2.Параметры схемы оставить без изменения.

3.3.Получить переходную характеристику по ошибке, задав последовательность команд (см. л.р. 3).

3.4.Задавая два значений Крег = Крс (Крс и 4*Крс) повторить п.п. 3.2.2-3.2.3 и получить два вида переходных характеристик.

3.5.Сделать вывод.

4.Исследование ошибки САР скорости с интегральным

регулятором и ступенчатым входным сигналом.

4.1. Для задания линейного входного сигнала х(t)=К2*t за-

дать параметры PID контроллера следующими:

Proportional: 0

Integral: К2

Derivat: 0.

4.2.Задать параметры схемы моделирования: звено РС

–PID - контроллер интегральное (Крег =К2), интегрирующее звено на входе схемы удалить, остальные звенья оста-

вить без изменения.

4.3.Получить переходную характеристику, задавая два значения Крег = Крс (Крс и 4*Крс). По переходной характеристике измерить установившееся значение hуст = εуст2.

4.4.Сделать вывод.

5. Исследование ошибки САР скорости с интеграль-

ным регулятором и линейным входным сигналом.

5.1. Задать на входе схемы ннтегрирующее звено.

80