Теория автоматического управления. лабораторный практикум. Харченко А.П

УДК 621.313

Харченко А.П. Теория автоматического управления: лабораторный практикум: учеб. пособие [Электронный ресурс]. – Электрон. текстовые и граф. данные (1,2 Мб) / А.П. Харченко. - Воронеж: ФГБОУ ВО «Воронежский государственный технический университет», 2017. – 1 электрон. опт. диск (CD-ROM) : цв. – Систем. требования : ПК 500 и выше ; 256 Мб ОЗУ ; Windows XP ; SVGA с разрешением 1024x768 ; Adobe Acrobat ; CD-ROM дисковод ; мышь. – Загл. с экрана.

В учебном пособии предложены математические модели элементов и систем автоматического управления. Рассмотрены вопросы анализа динамических и статических показателей качества управления.

Издание соответствует требованиям Федерального государственного образовательного стандарта высшего профессионального образования по направлению 15.03.05 “Кон- структорско-технологическое обеспечение машиностроительных производств”, дисциплине “Теория автоматического управления”.

Предназначено для студентов 3 курса.

Табл. 10. Ил. 33. Библиогр.: 3 назв.

Рецензенты: кафедра электроэнергетики Международного

института компьютерных технологий (зав. кафедрой д-р техн. наук, проф. А.Н. Анненков); канд. техн. наук, доц. В.А. Трубецкой

©Харченко А.П., 2017

©Оформление. ФГБОУ ВО

«Воронежский государственный технический университет», 2017

2

ВВЕДЕНИЕ

Теория автоматического управления (ТАУ) – это техническая дисциплина, основанная на использовании математического представления систем и их элементов.

ТАУ используется при проектировании современных технических систем, то есть описывает методы анализа и синтеза технических систем путем математического в настоящее время чаще компьютерного моделирования.

Математическое описание системы начинается с разделения ее на элементы, для которых должны быть составлены уравнения, описывающие их функционирования.

Уравнения составляют на основе анализа физических, механических, электрических и других процессов, протекающих в системе, с помощью законов электротехники, законов сохранения энергии, гидравлики и т.п.

Математической моделью называется система уравнений с достаточной точностью описывающая поведение объекта во времени и пространстве.

Следует отдавать себе отчет, что никакая математическая модель физической системы не является точной.

Необходимо стремится к тому, чтобы модель адекватно отражала поведение физической системы в области ее работоспособности и в тоже время была не слишком сложной, доступной для анализа и численного расчета.

Теория автоматического управления изучает свойства различных в основном технических систем с целью обеспечения наиболее благоприятных условий работы.

Автоматизация процессов заключается в проектировании специальных устройств, а в более широком смысле систем автоматического управления (САУ), которые должны обеспечивать выполнение возложенной задачи с желаемым качеством, двигаться по заданной траектории в пространстве и во времени. Необходимость обеспечения желае-

3

мого закона изменения какой-либо величины возникает в различных отраслях техники.

-металлорежущие станки – обработка детали по заданной программе с высокой точностью;

-робототехника – движение рабочего органа по заданной траектории в пространстве;

-металлургической и бумажной промышленности – поддержание толщины проката в пределах установленного допуска;

-электроснабжение – постоянство частоты и напряжения сети;

-авиации и судовождении – движение самолета или судна по заданному курсу и эффективной их работы в автоматическом режиме, т.е. без вмешательства человекаоператора.

В настоящее время интенсивно разрабатываются микроэлектронные средства автоматических систем, обеспечивающие высокое быстродействие и технологичность.

Одной из основных отличительных особенностей автоматических систем является выявление и практическое использование общих закономерностей, имеющихся в работе систем различной физической природы - механических, пневматических, гидравлических, электрических, электронных.

При проектировании современных технических систем

предлагаются современные методы анализа и синтеза технических систем путем компьютерного моделирования.

Лабораторный практикум предназначается для практической проверки основных положений ТАУ, закрепления у студентов теоретических знаний, получения навыков работы с пакетом прикладных программ для моделирования непрерывных процессов Matlab.

4

ЛАБОРАТОРНАЯ РАБОТА № 1

ИЗУЧЕНИЕ ПРОГРАММЫ MATLAB

Цель работы: Изучение системы инженерных расчетов программы Matlab и исследование временных характеристик редуктора, как пропорционального, интегрирующего и дифференцирующего типовых звеньев при типовых входных сигналах

В качестве инструмента для проведения лабораторных работ применяется пакет визуального моделирования SIMULINK системы инженерных и научных расчетов MATLAB.

Пакет SIMULINK позволяет реализовать математические модели объектов в виде структур и специальных функций для синтеза и анализа этих моделей.

Запуск SIMULINK можно произвести либо нажав кноп-

ку на панели меню командного окна , либо выбрав команду New Model в разделе File главного меню.

БИБЛИОТЕКА БЛОКОВ SIMULINK

Библиотека блоков SIMULINK представляет собой набор визуальных объектов, используя которые можно собирать, как из кубиков, произвольную конструкцию.

Для любого блока можно получать требуемое число копий, каждую из которых можно использовать автономно.

Для удобства работы пользователя библиотека блоков разбита на семь разделов.

Кратко опишем минимум блоков, который необходим для выполнения лабораторных работ по теории автоматического управления линейных непрерывных систем.

5

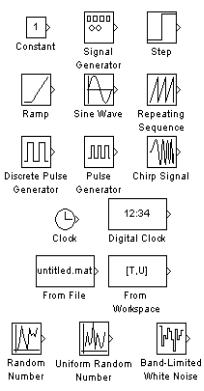
1. Раздел Sources (Источники)

Блоки в этом разделе, предназначены для формирования сигналов, обеспечивающих управление работой.

S–модели в целом или отдельных ее частей. Все блокиисточники, приведенные на рис. 1, имеют по одному выходу и не имеют входов.

Блок Constant формирует постоянную величину (скаляр, вектор или матрицу).

Блок Signal Generator со-

здает непрерывный сигнал произвольной формы.

Блок Step генерирует единичный дискретный сигнал с заданными параметрами.

Блок Ramp создает линейно возрастающий сигнал. Блок Sine Wave – генератор гармонических колебаний.

Блок Clock формирует непрерывный временной сигнал.

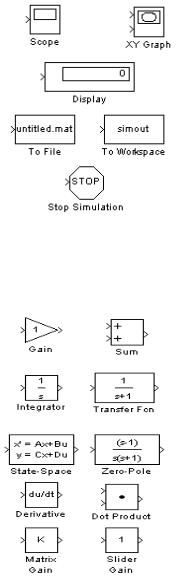
2. Раздел Sinks (Получатели)

Блоки, собранные в этом разделе, представлены на рис. 2. Блок Scope создает график зависимости величины от машинного времени. Блок XYGraph двумерный график в прямоугольной системе координат. Блок Display отображает численные значения величин. Блоки To File и To Workspace сохраняют промежуточные и/или выходные результаты моделирования в M-файл или рабочую область MATLAB соответ-

Рис. 2 ственно. Блок Stop Simulation позволяет прервать моделирование .

3. Раздел Linear (Линейные элементы)

Раздел содержит блоки, приведенные на рис. 3, предназначенные для описания линейных непрерывных систем. Блок Gain представляет собой "линейный усилитель" Блок Sum суммирует входные сигналы. Блок Integrator интегрирует входной сигнал по времени. Блок Transfer Fcn – апериодическое звено первого порядка. Блок Derivative вычисляет производную входного сигнала по времени.Блок Dot Products вычисляет скалярное произведение двух сигналов. Блок Matrix Gain – матричный усилитель (умножитель входного сигнала).

Рис. 3 Блок Slider Gain – позволяет менять коэффициент усиления.

7

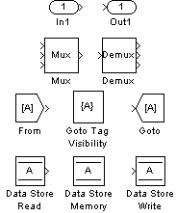
4. Раздел Connections (Соединительные узлы)

Большинство блоков данного раздела (см. рис. 4) предназначены для разработки S-моделей, содержащих модели более низкого уровня. Блоки In (Вход) и Out (Выход) обеспечивают "линейную" связь между подсистемами модели по информации.

Блок Mux объединяет входные величины в один линейный вектор. Блок Demux разделяет входной вектор на заданное число компонентов. Блоки Goto Tag Visibility (признак видимости), From (принять) и Goto (передать) используются совместно и предназначены для обмена данными между различными компонентами S – модели. Блоки Data Store Memory (память данных), Data Store Read (чтение данных) и Data Store Write (запись данных) также используются совместно и обеспечивают хранение данных на интервале моделирования.

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Математическое описание в теории автоматического управления сводится к передаточным функциям.

Передаточная функция находится из уравнения (уравнение элемента в операторной форме, где символ производной d/dt заменен оператором р или переменной s), как отношение выходного сигнала элемента Yвых(p) к входному сигналу Хвх(р).

Передаточные функции типовых динамических звеньев:

8

Пропорционального звена

W(p) = K1.

Интегрирующего звена

W(p) = K2 / р.

Дифференцирующего звена

W(p) = K3*р,

где К1-К3 – значения коэффициента передачи пропорционального, интегрирующего и дифференцирующего звеньев.

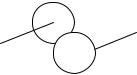
Кинематическая схема представляется единым редуктором с абсолютным жестким соединением.

Математическое описание редуктора при различных входных и выходных сигналах определяется следующим образом.

Рассмотрим условное обозначение редуктора, представленное на рис. 5 с указанием вида входных и выходных сигналов, то есть скорости Ω(t) или перемещения Ψ(t).

Ω1(t)

Ω2(t)

Ψ1(t) Ψ2(t)

Рис. 5. Условное обозначение редуктора

Примером пропорционального звена является редуктор, входной сигнал которого х(t)=Ω1(t) – скорость, выходной сигнала у(t)=Ω2(t) – скорость.

9

Уравнение в операторной форме примет следующий

вид:

Ω2(p)=k*Ω1(p)

Примером интегрирующего звена является редуктор входной сигнал которого х(t)=Ω1(t) – скорость, выходной сигнал у(t)= Ψ2(t) – перемещение.

Уравнение для редуктора, как интегрирующего звена, в операторной форме имеет следующий вид:

Ψ2(p)= К*1/р *Ω1(p).

Примером дифференцирующего звена является редуктор при входном сигнале х(t)=Ψ1(t) – перемещение, выходном сигнале у(t)= Ω2(t) – скорость.

Уравнение для редуктора, как дифференцирующего звена, в операторной форме имеет следующий вид:

Ω2(p)= К*p*Ψ1(p)

Программа Matlab позволяет исследовать временные (переходные и импульсные переходные) характеристики как в области Simulink, так и в рабочей области.

Математические модели элементов исследуемых САУ в подсистеме Simulink можно извлечь из библиотеки Continuous, источники сигналов (излучатели) из библиотеки Sources, индикаторы (приемники) из Sinks.

Временные характеристики математических моделей таких элементов, как дифференцирующее и форсирующее типовые звенья, исследуются только с помощью визуальных

блоков.

Переходная характеристика получается при решении дифференциального уравнения относительно выходного сигнала y(t)=h(t) с учетом закона изменения входного сигнала

х(t)=F(t).

10