Свободные колебания

Рассмотрим свободные колебания как частный случай затухающих колебаний. Предположим, что сопротивление среды настолько мало по сравнению с упругой силой пружины, что им при решении задач можно пренебречь. Тогда , следовательно, . Из (34) получаем уравнение свободных колебаний точки:

. (37)

Общее решение этого уравнения вытекает из (32), если в нем положить :

. (38)

Следовательно, свободные колебания точки являются гармоническими колебаниями. Период свободных колебаний находим из (34):

. (39)

Отсюда следует, что период свободных колебаний меньше периода затухающих колебаний.

Вынужденные колебания

Силы, вызывающие вынужденные колебания, называют возмущающими силами. В большинстве случаев возмущающие силы являются периодическими функциями времени. Ограничимся следующим видом возмущающей силы:

, (40)

где – амплитуда возмущающей силы, – ее частота, – начальная фаза.

Сопротивлением среды пренебрегаем. На точку, таким образом, действуют силы: .

Дифференциальное уравнение движения точки найдем из второго закона Ньютона в проекции на ось :

. (41)

Учитывая, как и раньше, и вводя обозначения ; из (41) получим:

. (42)

Это неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Общее решение таких уравнений складывается из двух решений: общего решения соответствующего однородного уравнения. Общее решение однородного уравнения. Общее решение однородного уравнения определяется из (31) или (32) соответственно при в виде:

или . (43)

Частное решение ищем в виде

. (44)

Дифференцируя (45) дважды по времени и подставляя в (42), находим неизвестный коэффициент , предполагая, что :

.

Следовательно, частное решение уравнения (42) есть

.

Общее решение принимает вид:

. (45)

Постоянные интегрирования определим из начальных условий задачи.

Пусть в начальный момент времени

: , . (46)

Общее решение (45) после удовлетворения начальных условий (46) приобретает вид:

. (47)

На основании данного решения получаем, что движение точки в рассматриваемом случае есть результат наложения трех видов колебаний. Первых два слагаемых определяют свободные колебания. Они зависят от начальных условий и имеют частоту свободных колебаний . Третье слагаемое не зависит от начальных условий, но зависят от возмущающей силы и частоты свободных колебаний. Движения, определяемые этими слагаемыми, называются вынужденными колебаниями, имеющими частоту свободных колебаний. Последнее слагаемое определяет вынужденные колебания. Они не зависят от начальных условий и имеют частоту возмущающей силы.

Перейдем к рассмотрению случая , при котором возникает так называемый резонанс.

Из теории интегрирования дифференциальных уравнений известно, что частное решение уравнения (42) в этом случае нужно искать в виде:

, (48)

где известные постоянные , находятся из (42). Однако можно предложить другой способ нахождения частного решения при резонансе. Т.к. решение (47) справедливо при значениях сколь угодно близких к , то решение при найдем как предельный случай. Применим правило Лопиталя к третьему и четвертому слагаемым в формуле (47), сумма которых при обращается в неопределенность вида :

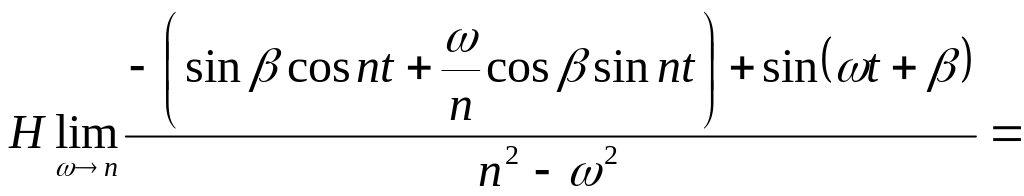
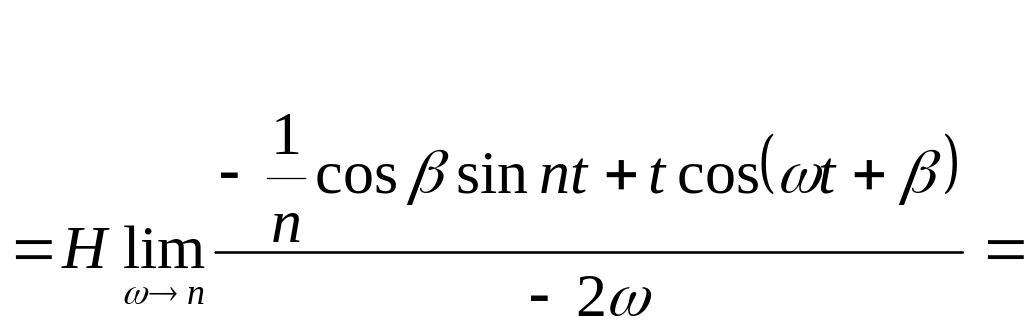
. (49)

Следовательно, движение точки в случае резонанса определяется выражением:

. (50)

Здесь последнее слагаемое определяет вынужденные колебания при резонансе, оно неограниченно возрастает с течением времени. Если рассматривать множитель перед косинусом в последнем числе как амплитуду вынужденных колебаний, то можно утверждать, что амплитуда вынужденных колебаний неограниченно растет пропорционально первой степени времени. График вынужденных колебаний при резонансе показан на рис.9.

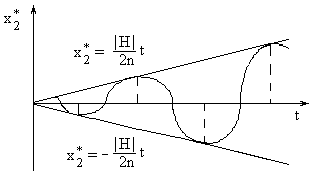
Рис. 9

Размахи колебаний с течением времени возрастают. В различных сооружениях при наступлении резонанса может произойти их разрушение. Здесь резонанс нежелателен. Вспомним, что мы пренебрегали силами сопротивления, которые при резонансе создают стабилизирующее действие и амплитуда вынужденных колебаний при резонансе имеет конечное значение при неограниченном возрастании времени . Однако и при наличии сил сопротивления приближение частоты возмущающих сил к частоте свободных колебаний может стать угрожающим для прочности сооружений. В некоторых областях техники, например, радиотехнике явление резонанса имеет доминирующее значение для работы прибора.