1.7. Элементы теории колебаний материальной точки

Рассмотрим простейшие колебательные движения материальной точки с одной степенью свободы: затухающие, свободные и вынужденные прямолинейные колебания.

Затухающие колебания

П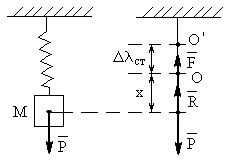 усть нужно определить закон колебания груза , прикрепленного к пружине (рис. 6) при следующих предположениях:

– вес пружины значительно меньше веса груза и им можно пренебречь;

–

Рис. 6

материал пружины подчиняется закону Гука;

– груз движется по прямой, совпадающей с осью пружины;

– груз можно принять за материальную точку;

– сила сопротивления среды, как следует из опытов, при малых скоростях пропорциональна первой степени скорости. Проекция этой силы на ось имеет вид:

, (21)

где коэффициент пропорциональности определяется из эксперимента.

Для решения задачи воспользуемся координатным способом определения движения точки, направляя ось вдоль пружины. Для упрощения решения выберем начало координат в точке, в которой находится движущаяся точка в тот момент времени, когда силы упругости пружины равна весу груза. Эта точка определяет положение статического равновесия точки . Произведем анализ сил, действующих на точку в произвольный момент времени. Кроме сил тяжести , на точку действует сила упругости пружины (восстанавливающая сила) и сила сопротивления среды , которая направлена против движения груза.

Согласно закону Гука, сила упругости пружины пропорциональна ее удлинению. Коэффициент пропорциональности называется жесткостью пружины. Удлинение пружины состоит из статического удлинения и динамического удлинения . Статическое удлинение соответствует переходу точки в положение так называемого статического равновесия из положения , соответствующего нерастянутой пружины. Проекция силы упругости на ось равна

. (22)

Дифференциальное уравнение движения точки имеет вид:

, (23)

где .

Представим (23) в виде:

, (24)

где

, . (25)

Дифференциальное уравнение (24) описывает движение точки в среде с сопротивлением. Это линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Согласно теории интегрирования таких уравнений, составим характеристическое уравнение

. (26)

Его корни

. (27)

Из (27) видно, что возможны три вида корней, а, следовательно, три вида движения точки. Рассмотрим их.

1) (случай большого сопротивления). Корни (27) действительные и различные. Общее решение уравнения (24) имеет вид:

. (28)

Исследуем эту функцию. Из (28) следует, что при , так как

Найдем экстремум этой функции:

,

,

.

Отсюда следует, что если имеют противоположные знаки, то существует один экстремум, а если одинаковые знаки, то экстремума нет. Таким образом, графики этой функции могут быть изображены кривыми, представленными на рис. 7. В этом случае движение точки называется апериодическим.

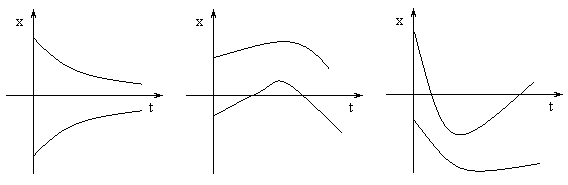
нет экстремума один максимум один минимум

Рис. 7

2) (предельный случай).

Корни характеристического уравнения действительные и равны: . Общий интеграл находится по формуле:

. (29)

Здесь, как и в первом случае, движение апериодическое. Точка с течением времени будет стремиться к положению статического равновесия при любых начальных условиях.

3) (случай малого сопротивления).

Характеристическое уравнение имеет комплексные корни

. (30)

Общее решение уравнения (24) имеет вид:

. (31)

Для придания соотношению (31) удобного для исследования вида, положим , , т.е. вместо постоянных , введем новые постоянные и . Получим

. (32)

Постоянные и определяются из начальных условий и называются амплитудой и начальной фазой колебаний точки.

Д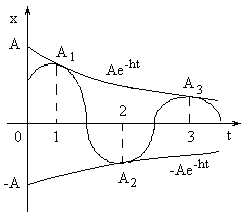 вижение точки, описываемое уравнением (31) или (32) называются затухающими колебаниями. Графически эти колебания можно иллюстрировать затухающей синусоидой, попеременно касающейся кривых и (рис.8).

Р

Рис. 8

асстояние между двумя соседними максимальными отклонениями точки называется размахом. Время , в течение которого точка совершает два размаха, называется периодом колебаний. Размахи колебаний уменьшаются, но отрезки 0-1, 1-2, 2-3, 3-4 и т.д. на оси будут равными величинами, т.к. период не зависит от времени и начальных условий, что будет доказано ниже. Найдем экстремумы функции (32), приравнивая ее первую производную к нулю:

.

Отсюда находим:

,

. (33)

Из (33) следует, что аргументы , двух соседних стационарных значений связаны соотношениями:

или

.

Т.к. представляет собой время одного размаха и является при малом сопротивлении величиной постоянной, то для периода колебаний получаем формулу:

. (34)

Отсюда видно, что при увеличении сопротивления период колебаний увеличивается.

Для амплитуд получаются формулы:

, . (35)

Из (35) находим:

. (36)

Из (36) видно, что величина амплитуд образует убывающую геометрическую прогрессию со знаменателем Величина, обратная , т.е. , называется декрементом затухания. Эта величина характеризует быстроту затухания колебаний, т.е. быстроту убывания координаты со временем. Величина называется логарифмическим декрементом затухания.