Законы сохранения кинетических моментов
Выведем законы сохранения кинетических моментов для системы, рассматривая материальную точку как механическую систему, у которой число точек равно единице. Естественно, что для одной материальной точки все действующие на нее силы являются внешними. Возможны следующие частные случаи теоремы об изменении кинетического момента системы.
1.
Если главный момент внешних сил системы
относительно точки
равен нулю, т. е.
,
то, согласно (109), кинетический момент
системы
относительно той же точки постоянен по
модулю и направлению, т. е.
. (110)
Этот частный случай теоремы об изменении кинетического момента системы называют законом сохранения кинетического момента. В проекциях на прямоугольные декартовы оси координат по этому закону
,
,
,
где
,
,
– постоянные величины.
Соотношения (110') являются первыми интегралами дифференциальных уравнений движения системы (88). Закон сохранения кинетического момента системы показывает, что одни внутренние силы не могут изменить кинетический момент системы, так же как они не изменяют ее количество движения.
2.
Если сумма моментов всех внешних сил
системы относительно оси
равна нулю, т.е.
,
то из (109') следует, что
. (111)
Следовательно, кинетический момент системы относительно какой-либо координатной оси постоянен, если сумма моментов внешних сил относительно этой оси равна нулю, что, в частности, наблюдается, когда внешние силы параллельны оси или пересекают ее. В частном случае для тела или системы тел, которые все вместе могут вращаться вокруг неподвижной оси, и если при этом
,
то
,
или
,
(112)
где
и
– момент инерции системы тел и их угловая
скорость относительно оси вращения в
произвольный момент времени
;
и
– момент инерции тел и их угловая
скорость в момент времени, выбранный
за начальный.
Дифференциальное уравнение вращения твердого тела вокруг неподвижной оси
И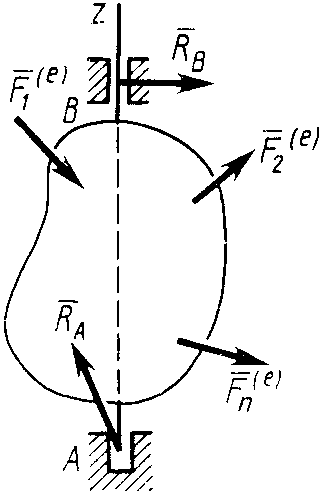
з
теоремы об изменении кинетического
момента (109') получим дифференциальное
уравнение вращения твердого тела вокруг
неподвижной оси
(рис. 39). Имеем
.
Для случая вращения твердого тела вокруг неподвижной оси, согласно (106), имеем
Рис. 39
где
– постоянный для твердого тела момент
инерции относительно неподвижной оси
вращения;
– угловая скорость. Учитывая это,
получаем
.
Если
ввести угол поворота тела
,
то, учитывая, что
,
имеем
.
Это и есть дифференциальное уравнение вращения твердого тела вокруг неподвижной оси. Оно полностью аналогично дифференциальному уравнению поступательного движения твердого тела в проекции на какую-либо ось, например на ось .
В дифференциальное уравнение вращения тела вокруг неподвижной оси вместо координаты входит угол поворота , вместо массы тела – момент инерции относительно оси вращения вместо суммы проекций внешних сил на ось – сумма моментов внешних сил относительно оси вращения или так называемый вращательный момент внешних сил.
Реакции
подшипников
и
оси вращения являются внешними силами,
но их моменты относительно оси вращения
равны нулю, так как они пересекают ось,
если пренебречь силами трения.
В частном случае, когда
,
то
,
т. е. вращение тела происходит с постоянным угловым ускорением.
Если
,
то
,
и
.
Это случай равномерного вращения тела по инерции без действия вращательного момента внешних сил.
Дифференциальное уравнение вращательного движения твердого тела в общем случае позволяет решать две основные задачи: по заданному вращению тела определять вращающий момент внешних сил и по заданному вращательному моменту и начальным условиям находить вращение тела. При решении второй задачи для нахождения угла поворота как функции времени приходится интегрировать дифференциальное уравнение вращательного движения. Методы его интегрирования полностью аналогичны рассмотренным выше методам интегрирования дифференциального уравнения прямолинейного движения точки.
Рассмотрим в качестве примера вращательное движение физического и математического маятников.
Физическим
маятником называется тело произвольной
формы, которое может вращаться вокруг
горизонтальной оси под действием силы
тяжести (рис. 40). Внешние силы здесь: вес
и реакции оси подвеса
.
Вес приложен в центре тяжести маятника.
Главный
момент всех внешних сил равен моменту
силы
,
т.к. моменты сил
равны нулю, поскольку радиус- в
Рис. 40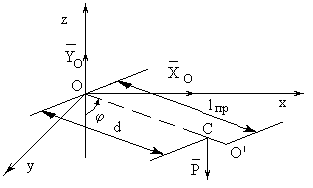
.
Подставляя это значение в дифференциальное уравнение вращения твердого тела вокруг неподвижной оси, получаем
,
или
.
Это
дифференциальное уравнение движения
физического маятника. Ограничения
рассмотренных малых колебаний маятника,
для которых
.
Тогда получим
,
где
.
Таким образом, получаем такое же уравнение, как для свободного колебания точки, рассмотренного в разделе 1.7. Следовательно, решением этого уравнения является
.
Т.е. это гармонические колебания. Здесь – амплитуда колебаний, – начальная фаза, – круговая частота колебаний.
и определяются из начальных условий. Период колебаний, т.е. промежуток времени, протекающий между двумя последовательными прохождениями центра масс маятника через некоторое фиксированное положение на его траектории в определенном фиксированном направлении, определяется по формуле
.
Отсюда следует, что период малых колебаний не зависит от начальных условий. Такие колебания называются изохорными.
Математическим маятником называется материальная точка, подвижная к горизонтальной оси посредством идеальной нити или идеального стержня и движущаяся под действием силы тяжести.
Пусть длина маятника , вес . Положение маятника определяется углом отклонения от вертикали .
Для
математического маятника
.
Соответственно получаем:
,
где теперь
.
Период колебаний
.
Отсюда
следует, что период колебаний физического
маятника совпадает с периодом колебаний
математического маятника, длина которого
,
эта длина называется приведенной длиной
физического маятника. Центром колебаний
физического маятника называется точка
,
лежащая на прямой
(рис. 40) и отстоящая от точки
на расстоянии
.