§ 5. Степенные ряды в приближенных вычислениях

Вычисление значений функции. Пусть дан степенной ряд функции . Задача вычисления значения этой функции заключается в отыскании суммы ряда при заданном значении аргумента. Ограничиваясь определенным числом членов ряда, находим значение функции с точностью, которую можно установить путем оценивания остатка числового ряда либо остаточного члена формул Тейлора или Маклорена. Если данный ряд знакопостоянный, то ряд, составленный из отброшенных членов, сравнивают с бесконечно убывающей геометрической прогрессией. В случае знакочередующегося ряда используется оценка , где - первый из отброшенных членов ряда.

5.1.Оценить погрешность приближенного равенства

Решение. Погрешность этого приближенного равенства

определяется суммой членов, следующих после в разложении :

,

или

Заменив каждый из сомножителей ,… меньшей величиной , получим неравенство

Просуммируем бесконечно убывающую геометрическую прогрессию, получим:

, т.е.

5. 2.Вычислить с точностью до 0,00001.

Решение. Используя разложение в ряд, получаем

.

Определим число так, чтобы погрешность приближенного равенства

не превышала 0,00001. Воспользуемся оценкой погрешности, данной в предыдущем примере. Полагаем , тогда:

т.е. .

Путем подбора определим, при каком значении будет

выполняться неравенство . Пусть , тогда , т.е. . Пусть , тогда , т.е. . Принимаем .

.

Вычисляем каждое слагаемое с точностью до 0,000001, для того чтобы при суммировании не получить погрешность, превышающую 0,00001. Окончательно получаем .

5.3. Вычислить с точностью до 0,00001.

Решение. Имеем

.

Получен знакочередующийся ряд, удовлетворяющий условиям сходимости признака Лейбница, поэтому допускаемая погрешность по абсолютной величине должна быть меньше первого из отброшенных членов ряда. Нетрудно видеть, что , поэтому первый из отброшенных членов равен и . Вычисляем сумму и получаем .

5.4. Пользуясь разложением в ряд, вычислить с точностью до 0,0001 .

Решение. .

Достаточно взять три члена ряда, так как Тогда

5.5. Вычислить с точностью до 0,0001.

Решение. Воспользуемся разложением в ряд, полагая . Имеем

.

Четвертый и следующие за ним члены отбрасываем, так как четвертый член меньше 0,0001. Итак

5.6. Вычислить с точностью до 0,001.

Решение. Так как является ближайшим к числу 130 кубом целого числа, то целесообразно число 130 представить в виде суммы двух слагаемых: . Тогда

Четвертый член меньше , поэтому его и следующие за ним члены можно отбросить. Итак,

, т.е. .

5.7. Вычислить с точностью до 0,0001.

Решение. Воспользуемся разложением в ряд:

,

или , откуда

Вычислить указанную величину приближенно с заданной степенью точности , воспользовавшись разложением в степенной ряд соответствующим образом подобранной функции.

5.8. . 5.9.

5.10. . 5.11. .

5.12. , . 5.13.

5.14. 5.15.

5.16. , 5.17.

Ответы: 5.8. 3,017. 5.9. 0,340. 5.10. 0,84147. 5.11. 1,3956.

5.12. 1,140. 5.13. 0,302. 5.14. 0,464. 5.15. 1,0986. 5.16. 0,999. 5.17. 0,3679.

Вычисление интегралов. Так как степенные ряды сходятся равномерно на любом отрезке, лежащем внутри их интервала сходимости, то с помощью разложений функций в степенные ряды можно находить неопределенные интегралы в виде степенных рядов и приближенно вычислять соответствующие определенные интегралы.

5.18. Вычислить с точностью

Решение. Воспользуемся разложением

.

Заменив в нем на , получим ряд

.

Данный ряд сходится на всей числовой прямой, поэтому его можно всюду почленно интегрировать. Следовательно,

, поскольку уже третий член полученного знакочередующегося ряда меньше

5.19. Найти интеграл в виде степенного ряда и указать область его сходимости.

Решение. Воспользуемся разложением

,

получим ряд для подынтегральной функции

.

Он сходится на всей числовой прямой, и, следовательно, его можно почленно интегрировать:

.

Поскольку при интегрировании степенного ряда его интервал сходимости не изменяется, то полученный ряд сходится также на всей числовой прямой.

Используя разложение подынтегральной функции в степенной ряд, вычислить указанный определенный интеграл с точностью до .

5.20. . 5.21. .

5.22. . 5.23. .

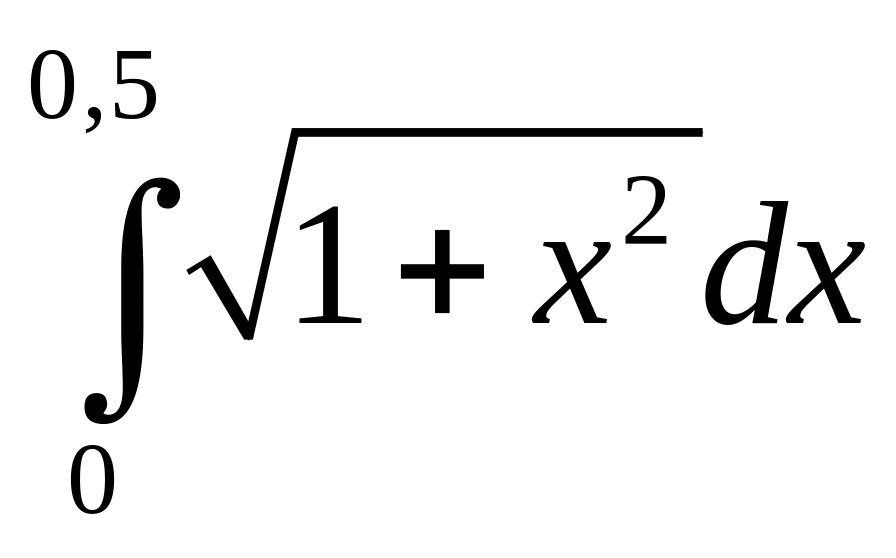5.24. . 5.25. .

5.26. . 5.27. .

5.28. 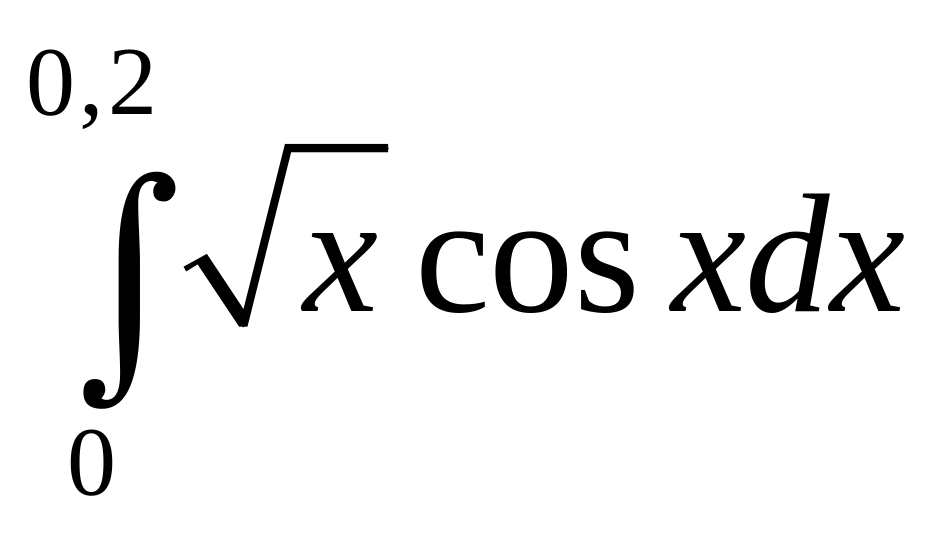. 5.29.

Ответы: 5.20. 0,070. 5.21. 0,223. 5.22. 0,162 5.23. 0,480.

5.24. 0,054. 5.25. 0,484. 5.26. 0,487. 5.27. 0,156. 5.28. 0,059.

5.29. 0,103.

Приближенное решение дифференциальных уравнений. В случае, когда точно проинтегрировать дифференциальное уравнение с помощью элементарных функций не удается, его решение удобно искать в виде степенного ряда, например ряда Тейлора или Маклорена.

При решении задачи Коши

,

используется ряд Тейлора , где , а остальные производные находятся путем последовательного дифференцирования уравнения и подстановки начальных данных в выражения для этих производных.

Решение задачи Коши для дифференциального уравнения можно также искать в виде разложения в степенной ряд

с неопределенными коэффициентами .

5.30. Найти пять первых членов разложения в степенной ряд решения , если .

Решение. Из данного уравнения находим, что . Дифференцируем исходное уравнение:

и т.д. Подставляя найденные значения производных в ряд

Тейлора, получаем

.

5.31. Найти шесть первых членов разложения в степенной ряд решения дифференциального уравнения , удовлетворяющего начальным условиям .

Решение. Подставим в уравнение начальные условия, получим:

Дифференцируя исходное уравнение, последовательно находим:

Подставляя найденные значения производных в ряд Маклорена, получаем

.

5.32.Используя ряд

,

записать четыре первых ненулевых члена разложения в

степенной ряд решения задачи Коши

Решение. В ряде

полагаем , с учетом начального условия находим, что . Продифференцируем ряд

и подставим полученную производную , а также в виде

ряда в данное дифференциальное уравнение. Тогда

+

Теперь в правой и левой частях последнего равенства приравняем коэффициенты при одинаковых степенях разности (т.е. при . Получаем уравнения:

из которых, учитывая, что , находим:

Следовательно, искомое разложение решения имеет вид

.

Найти разложение в степенной ряд по степеням решения дифференциального уравнения (записать три первых, отличных от нуля, члена этого разложения

5.33. 5.34. 5.35. 5.36. 5.37.

Методом последовательного дифференцирования найти первые членов разложения в степенной ряд решения дифференциального уравнения при указанных начальных условиях.

5.38.

5.39.

5.40.

5.41.

5.42.

Ответы: 5.33. . 5.34. .

5.35. . 5.36. .

5.37. . 5.38. .

5.39. .

5.40. .

5.41.

5.42.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Пискунов Н.С. Дифференциальные и интегральные исчисления / Н.С. Пискунов.- М.: Наука, 2001.Т.2.- 576 с.

2. Воробьев Н.Н. Теория рядов/ Н.Н. Воробьев. - М.: Наука, 1986. - 408 с.

3. Власова Е.А. Ряды / Е.А. Власова.- М.: Изд-во МГТУ им. Н.Э. Баумана, 2002.-612 с.

4. Романовский П.И. Ряды Фурье. Теория поля. Аналитические и специальные функции. Преобразование Лапласа / П.И. Романовский. - М.: Наука, 1980.-336 с.

5. Данко П.Е. Высшая математика в упражнениях и задачах / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – М.: «Оникс 21 век» «Мир и образование», 2003. Ч. 2.

6. Индивидуальные задания по высшей математике: Ряды. Кратные и криволинейные интегралы. Элементы теории поля: учеб. пособие/ А. П. Рябушко и др.; под общ. ред. А. П. Рябушко.- 3-е изд.- Минск.: Выш. шк., 2005.-367 с.

7. Зимина О.В. Высшая математика./ О.В. Зимина, А.И. Кириллов, Т.А. Сальникова.- М.: Физико-математическая литература, 2001.-368 с.

8. Ефимов А.В. Сборник задач по математике для втузов/ А.В. Ефимов, Б. П. Демидович; под ред. А.В. Ефимова. - М.: Наука,1986. –Ч.2.-368 с.