§ 2. Функциональные ряды

Ряд , члены которого –

функции от , называется функциональным. Совокупность

значений , при которых функции определены и ряд сходится, называется областью сходимости функционального ряда. Областью сходимости функционального ряда чаще всего бывает какой-либо промежуток оси . Каждому значению из области сходимости соответствует определенное значение величины . Эту величину, являющуюся функцией , называют суммой функционального ряда и обозначают .

Представим сумму ряда в виде , где

- остаток функционального ряда. В области сходимости функционального ряда , а .

Сходящийся функциональный ряд называется равномерно сходящимся в некоторой области , если для каждого сколь угодно малого числа найдется такое целое положительное число , что при выполняется неравенство для любого из области .

Сформулируем достаточный признак равномерной сходимости функционального ряда – признак Вейерштрасса.

Если функции по абсолютной величине не превосходят в некоторой области положительных чисел причем числовой ряд сходится, то функциональный ряд в этой области сходится равномерно.

При этом сходящийся числовой ряд называется мажорантным (мажорирующим) рядом, а соответствующий функциональный ряд называется мажорируемым в области .

Равномерно сходящиеся ряды обладают некоторыми общими свойствами:

1) если члены равномерно сходящегося ряда непрерывны на некотором отрезке, то его сумма также непрерывна на этом отрезке;

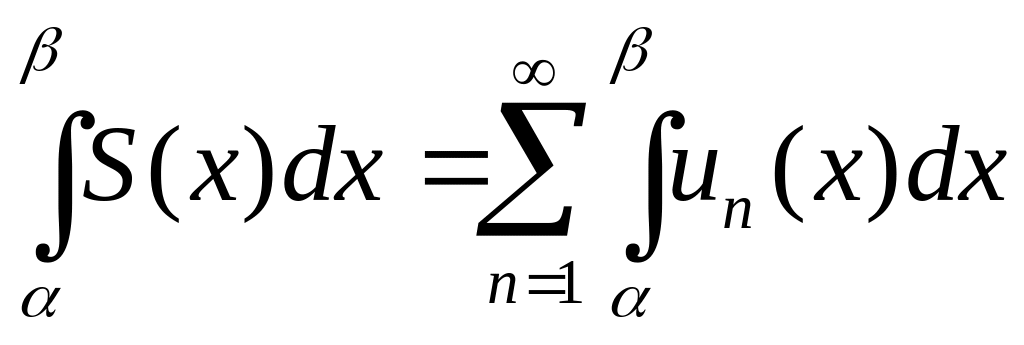2) если члены ряда непрерывны на отрезке и ряд равномерно сходится на этом отрезке, то в случае, когда , верно равенство: , где

- сумма ряда ;

3) если ряд , составленный из функций, имеющих непрерывные производные на отрезке , сходится на этом отрезке к сумме и ряд равномерно сходится на

том же отрезке, то .

2.1. Найти область сходимости функционального ряда

= .

Решение. Данный ряд, определенный при , является суммой членов геометрической прогрессии со знаменателем . Такой ряд сходится, если , т.е. при . Поэтому областью сходимости исследуемого ряда является интервал ( .

2.2. Найти область сходимости функционального ряда

.

Решение. Используем признак Даламбера:

;

;

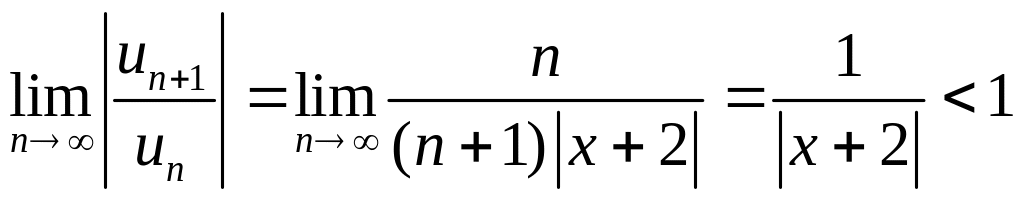Границы двух найденных интервалов исследуем особо.

При получим знакочередующийся числовой ряд с общим членом , который сходится согласно признаку Лейбница.

При получим расходящийся гармонический ряд.

Следовательно, область сходимости данного ряда состоит из двух бесконечных интервалов

2.3. Найти область сходимости ряда

.

Решение. Находим общий член ряда . Если , то ; так как , то ряд расходится. Если , то также получаем расходящийся ряд

.

Если , то члены заданного ряда меньше членов беско-

нечно убывающей геометрической прогрессии , т.е. ряд сходится.

Итак, область сходимости ряда определяется неравенством

. Отсюда следует, что ряд сходится при

2.4. Найти сумму ряда .

Решение. При данный ряд сходится (так как ), значит его можно почленно дифференцировать в интервале сходимости. Обозначив сумму ряда через , имеем

.

Так как , полученный ряд есть сумма членов убывающей геометрической прогрессии со знаменателем и его сумма . Проинтегрировав ряд из производных, найдем сумму данного ряда:

, при .

2.5. Найти сумму ряда и указать область сходимости ряда к этой сумме.

Решение. Находим область сходимости ряда. По признаку Коши интервал сходимости определяется неравенством В граничных точках при ряд расходится, при ряд сходится условно. Следовательно, данный ряд сходится при всех Сделаем замену . Получим геометрический ряд с областью сходимости

[-1,1). Используем формулу для вычисления суммы членов

бесконечно убывающей геометрической прогрессии

Кроме того, Учитывая, что степенной ряд можно почленно интегрировать на любом отрезке , целиком принадлежащем интервалу сходимости, получаем

Заметим, что так как ряд сходится в граничной точке , то его сумма непрерывна в этой точке (справа). Следовательно, при всех Заменяя на , получаем при .

Найти область сходимости ряда:

2.6. . 2.7. . 2.8. . 2.9. .

Построив мажорирующий ряд, доказать равномерную сходимость данного ряда в указанном промежутке.

2.10. .2.11. .

2.12. . 2.13. .

Найти суммы функциональных рядов и указать области их сходимости к этим суммам.

2.14. 2.15. 2.16.

2.17. 2.18. 2.19.

Ответы: 2.6. .2.7.

2.8. .2.9. 0,1 .

2.14.

2.15.

2.16.

2.17. 2.18.

2.19.