§ 3. Степенные ряды
Функциональный ряд вида
,
где
-
действительные числа, называется
степенным.
Основное свойство степенных рядов
состоит в том, что если степенной ряд
сходится при
,
то он сходится (и притом абсолютно) при
всяком значении
,
удовлетворяющем неравенству
(теорема
Абеля).
Одним из следствий теоремы Абеля
является факт существования для всякого
степенного ряда интервала сходимости
,
или
с центром в точке
,
внутри которого степенной ряд абсолютно
сходится и вне которого он расходится.
На концах интервала сходимости (в точках
)
различные степенные ряды ведут себя
по-разному: одни сходятся абсолютно на
обоих концах, другие- либо условно
сходятся на обоих концах, либо на одном
из них условно сходятся, на другом
расходятся, третьи расходятся на обоих
концах.
Число
-
половина длины интервала сходимости -
называется радиусом сходимости
степенного ряда. В частных случаях
радиус сходимости ряда
может быть равен нулю или бесконечности.
Если
,
то степенной ряд сходится лишь при
;
если же
,
то ряд сходится на всей числовой оси.
Для отыскания интервала и радиуса сходимости степенного
ряда можно пользоваться одним из следующих способов.
1. Если среди коэффициентов ряда
нет
равных нулю, т.е. ряд содержит все целые
положительные степени разности
,
то
,
при условии, что этот предел (конечный
или бесконечный) существует.
2. Если исходный ряд имеет вид
,
(где - некоторое определенное целое положительное число:
2,3,…), то
.
3. Если среди коэффициентов ряда есть
равные нулю и последовательность
оставшихся в ряде показателей степеней
разности
любая (т.е. не образует арифметическую
прогрессию как в предыдущем случае), то
радиус сходимости можно находить по
формуле
в которой используются только значения
,
отличные от нуля.
4. Во всех случаях интервал сходимости можно находить, применяя непосредственно признак Даламбера или признак Коши к ряду, составленному из абсолютных величин членов исходного ряда.
Отметим следующее свойство степенных рядов: ряды, полученные почленным дифференцированием и интегрированием степенного ряда, имеют тот же интервал сходимости и их сумма внутри интервала сходимости равна соответственно производной и интегралу от суммы первоначального ряда.
Таким образом, если
,
то
,
где
.
Операции почленного дифференцирования и интегрирования можно производить над степенным рядом сколько угодно раз. Следовательно, сумма степенного ряда внутри его интервала сходимости является бесконечно дифференцируемой функцией.
3.1. Исследовать сходимость степенного ряда
.
Решение. Здесь
.
Найдем радиус сходимости ряда:
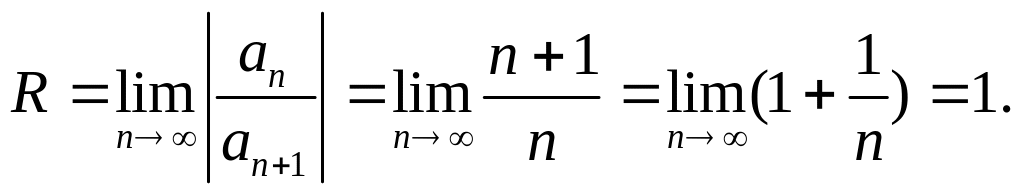Следовательно, ряд сходится для значений
,
удовлетворяющих неравенству
Исследуем сходимость ряда на концах
промежутка. При
,
получаем гармонический ряд
,
который, как известно, расходится. При
получаем ряд
.
Этот ряд сходится условно, так как
удовлетворяет условиям признака
Лейбница. Итак, область сходимости
степенного ряда определяется двойным
неравенством
.
3.2. Исследовать сходимость степенного ряда
.
Решение. Здесь
.
Найдем радиус сходимости ряда:
Следовательно, ряд сходится, если
,
т.е.
Исследуем сходимость ряда на концах
промежутка. При
,
получаем ряд
,
который сходится, так как ряд
сходится при
.
При
получаем ряд
.
Этот ряд сходится (и притом абсолютно),
так как сходится ряд из абсолютных
величин его членов. Итак, область
сходимости степенного ряда определяется
двойным неравенством
.
3.3. Исследовать сходимость степенного ряда
.
Решение. Здесь
.
Найдем радиус сходимости ряда:
Следовательно, ряд сходится при любом значении .
3. 4. Исследовать сходимость степенного ряда
.
Решение. Ряд является геометрической
прогрессией со знаменателем
.
Он сходится, если
,
и расходится, если
.Следовательно,
промежуток сходимости ряда определяется
двойным неравенством
Исследовать сходимость степенного ряда
Решение. Применим признак Даламбера, учитывая, что
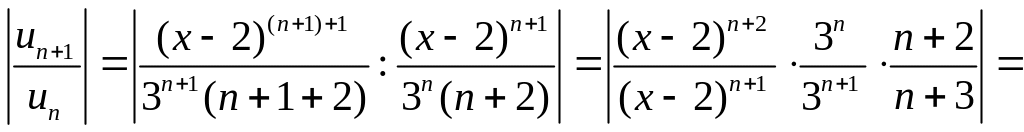
получим
.
Отсюда, при выполнении неравенства
по признаку Даламбера ряд сходится.
Преобразуем последнее неравенство
Отсюда, при выполнении неравенства по признаку Даламбера ряд сходится. Преобразуем последнее неравенство
.
Итак, при
ряд сходится абсолютно, а при
-
расходится. Следовательно,
-
интервал сходимости данного ряда.
Исследуем сходимость ряда на концах
этого интервала, т.е. в точках
и
.
При получим ряд
Применяя второй признак сравнения, сравниваем этот ряд с гармоническим рядом :
Поскольку ряд расходится, а полученный предел не ра-
вен нулю, то ряд
расходится.
При получим ряд
Этот ряд не является абсолютно сходящимся, так как ряд , составленный из абсолютных величин членов данного ряда, расходится.
Выясним, сходится ли данный знакочередующийся ряд, используя признак Лейбница.
1) Очевидно, неравенство
выполнено для всех
.
2)
Для знакочередующегося ряда
выполнены
оба условия признака Лейбница, значит,
данный ряд сходится. Так как он не
является абсолютно сходящимся, то ряд
сходится условно. Окончательно получим,
область сходимости исходного ряда –
промежуток
3.6. Найти сумму ряда
,
продифференцировав почленно ряд
Решение. Воспользовавшись формулой
суммы членов бесконечно убывающей
геометрической прогрессии
,
получаем
Остается продифференцировать полученное
равенство:
Найти области сходимости степенных рядов:
3.7.
3.8.
3.9.
3.10.
3.11.
3.12.
3.13.
3.14.
3.15.
3.16.
Применив почленное интегрирование и дифференцирова-
ние, найти суммы указанных радов:
3.17.
3.18.
3.19.
Ответы. 3.7.
3.8.
3.9.
3.10.
3.11.
3.12.
3.13.
3.14.
3.15.
.
3.16.
.
3.17.
3.18.
3.19.
.