§ 4.Разложение функций в степенные ряды

Всякая функция, бесконечно дифференцируемая в интервале , т.е. , может быть разложена в этом интервале в сходящийся к ней бесконечный степенной ряд Тейлора

,

если в этом интервале выполняется условие

,

где - остаточный член формулы Тейлора, .

При получаем так называемый ряд Маклорена:

.

Если в некотором интервале, содержащем точку , при любом выполняется неравенство , где - положительная постоянная, то и функция разложима в ряд Тейлора.

Приведем разложения в ряд Тейлора следующих функций:

1)

2)

3)

4)

5)

6)

7)

8) биномиальный ряд:

.

Это последнее разложение применимо в следующих случаях:

при если

при если

при если .

В общем случае разложение функций в степенные ряды основано на использовании рядов Тейлора или Маклорена. На практике степенные ряды многих функций можно найти формально, используя ряды (1-8) или формулу для суммы членов геометрической прогрессии. Иногда при разложении полезно пользоваться почленным дифференцированием или интегрированием рядов. В интервале сходимости ряды сходятся к соответствующим функциям.

4.1. Разложить по степеням разности функцию .

Решение. Для того чтобы воспользоваться формулой Тейлора при , найдем:

и т.д.

Следовательно,

4.2. Разложить в ряд по степеням .

Решение. Воспользуемся равенством . Правую часть этого равенства можно рассматривать как сумму бесконечно убывающей геометрической прогрессии с первым членом и знаменателем . Отсюда получаем

, т.е.

.

Так как , то

4.3. Разложить в ряд Маклорена функцию

Решение. Разложим данную функцию на сумму простейших рациональных дробей:

Поскольку

то

Так как ряд сходится при , а ряд сходится при , то ряд

сходится к данной функции при .

4.4. Разложить в степенной ряд функцию .

Решение. Найдем значения функции и ее производных при

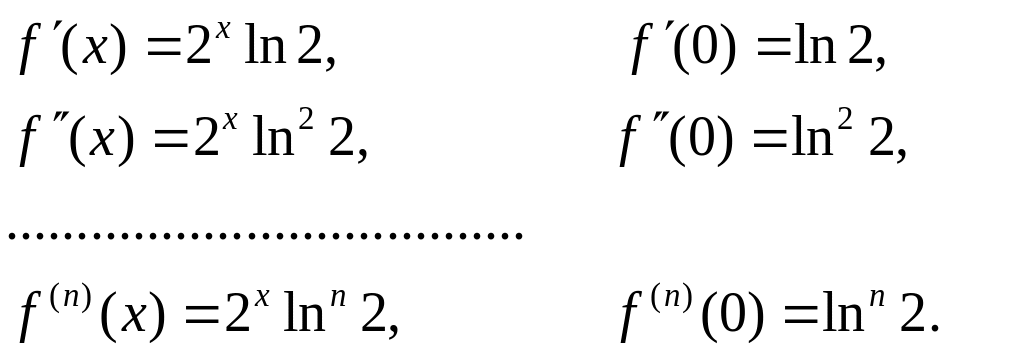
Так как , то при фиксированном имеет место неравенство при любом . Следовательно, функция может быть представлена в виде суммы ряда Тейлора:

.

В данном случае

Это разложение можно получить и иначе: достаточно в разложении заменить на .

4.5. Разложить в степенной ряд функцию .

Решение. В разложении

заменяем на , получаем

.

4.6. Разложить в ряд по степеням .

Решение. В разложении

заменяем на , получаем

.

4.7. Разложить в степенной ряд функцию .

Решение. Заметим, что .Рассмотрим ряд

.

Данный ряд сходится при , значит, его можно

почленно интегрировать на любом отрезке . Следовательно,

, т.е. получили ряд, сходящийся к данной функции при

4.8. Разложить по степеням многочлен

4.9. Разложить по степеням функцию и найти область сходимости полученного ряда.

4.10. Разложить по степеням функцию и найти область сходимости этого ряда.

4.11. Разложить по степеням функцию . Найти область сходимости этого ряда.

Разложить в ряд Маклорена функцию . Указать область сходимости полученного ряда к этой функции.

4.12. . 4.13.

4.14. . 4.15. .

4.16. 4.17. .

4.18. 4.19. .

Ответы:

4.8.

4.9.

4.10.

4.11.

4.12. 4.13. .

4.14. . 4.15.

4.16. . 4.17. .

4.18. 4.19. .