ФГБОУ ВПО "Воронежский государственный

технический университет"

Кафедра высшей математики и

физико-математического моделирования

Методические указания

для организации самостоятельной работы студентов по изучению раздела «РЯДЫ» курса «Математический анализ» по направлению подготовки бакалавров 230100 «Информатика и вычислительная техника», 090301.65 «Компьютерная безопасность» очной формы обучения

Воронеж 2014

Составители: канд.физ-мат.наук Е.Г.Глушко,

канд.физ-мат.наук А.П. Дубровская,

канд.физ-мат.наук Е.Н. Провоторова

УДК 517.9

Методические указания для организации самостоятельной работы студентов по изучению раздела «Ряды» курса «Математический анализ» по направлению подготовки бакалавров 230100 «Информатика и вычислительная техника», 090301.65 «Компьютерная безопасность» очной формы обучения / ФГБОУ ВПО "Воронежский государственный технический университет"; Составители: канд.физ-мат.наук Е.Г.Глушко, канд.физ-мат.наук А.П. Дубровская, канд.физ-мат.наук Е.Н. Провоторова. Воронеж, 2014. 43 с.

В методических указаниях содержатся краткие сведения по разделу «Ряды», приводится большое количество решенных типовых задач и задачи для самостоятельного решения студентами на практических занятиях и домашних заданий. Издание соответствует требованиям Государственного стандарта высшего профессионального образования по направлениям 230100 «Информатика и вычислительная техника», 090301.65 «Компьютерная безопасность».

Методические указания подготовлены в электронном виде в текстовом редакторе MS Word 2007 и содержатся в файле Ряды2.doc.

Ил. 6. Библиогр.: 7 назв.

Рецензент канд.физ-мат.наук Л.Д. Кретова

Ответственный за выпуск зав. кафедрой д-р физ.-мат.наук, проф. И.Л. Батаронов

Печатается по решению редакционно-издательского совета Воронежского государственного технического университета.

ФГБОУ ВПО "Воронежский

государственный технический

университет",2014

ВВЕДЕНИЕ

Методические указания посвящены теории рядов - важному разделу математического анализа, широко применяемому в различного рода исследованиях и вычислениях как в самой математике, так и во многих ее приложениях. Под общим термином «ряд» объединены определенные математические конструкции, применяемые к объектам различной природы: действительным и комплексным числам, функциям.

§1. Числовые ряды

Пусть где - бесконечная числовая последовательность. Выражение

называется бесконечным числовым рядом, а числа - членами ряда; называется общим

членом ряда. Ряд часто записывают в виде .

Сумму первых членов числового ряда обозначают через и называют -й частичной суммой ряда:

Ряд называется сходящимся, если его я частичная сумма , при неограниченном возрастании стремится к конечному пределу, т.е. если Число называют суммой ряда. Если же я частичная сумма ряда при не стремится к конечному пределу, то ряд называется расходящимся.

Ряд

составленный из членов любой убывающей геометрической прогрессии, является сходящимся и имеет сумму .

Ряд называемый гармоническим,

расходится.

Приведем основные теоремы о сходящихся рядах.

1. Если сходится ряд , то сходится и ряд получаемый из данного ряда отбрасыванием первых членов (этот последний ряд называют -м остатком исходного ряда); наоборот, из сходимости -го остатка ряда вытекает сходимость данного ряда.

2. Если сходится ряд и суммой его является число , то сходится и ряд , причем сумма последнего ряда равна

3. Если сходятся ряды , имеющие соответственно суммы и , то сходится и ряд причем сумма последнего ряда равна

4. Если ряд сходится, то , т.е. при

предел общего члена сходящегося ряда равен нулю (необходимый признак сходимости ряда).

Таким образом, если , то ряд расходится.

Перечислим важнейшие признаки сходимости и расходимости рядов с положительными членами.

Первый признак сравнения. Пусть даны два ряда с положительными членами:

(1)

и

(2)

причем каждый член ряда (1) не превосходит соответствующего члена ряда (2), т.е. Тогда, если сходится ряд (2), то сходится и ряд (1); если расходится ряд (1), то расходится и ряд (2).

Этот признак остается в силе, если неравенства , выполняются не при всех , а лишь начиная с некоторого номера

Второй признак сравнения. Если существует конечный и отличный от нуля предел , то оба ряда и одновременно сходятся или одновременно расходятся.

При применении признаков сравнения в качестве эталонного ряда используют один из следующих рядов:

а) обобщенный гармонический ряд , который сходится при и расходится при

б) геометрический ряд , который сходится при

и расходится при ( - некоторое положительное число).

Для оценки общего члена ряда используют неравенства:

, и т.д.

Признак Даламбера. Если для ряда существует , то этот ряд сходится при и расходится при .

При следует применить другой признак сходимости.

Признак Коши. Если для ряда существует , то этот ряд сходится при и расходится при .

При следует применить другой признак сходимости.

Интегральный признак. Если при - непрерывная, положительная и монотонно убывающая функция, то ряд , где , сходится или расходится в зависимости от того, сходится или расходится интеграл

Рассмотрим теперь ряды, члены которых имеют разные знаки.

Знакочередующимся рядом называется ряд вида

,

где

Признак сходимости знакочередующегося ряда (признак Лейбница). Знакочередующийся ряд сходится, если абсолютные величины его членов убывают, а общий член стремится к нулю, т.е. если выполняются следующие два условия:

1) и 2) .

Возьмем -ю частичную сумму знакочередующегося ряда, для которого выполняется признак Лейбница: Пусть - -й остаток ряда. Его можно записать как разность между суммой ряда и -й частичной суммой , т.е. . Нетрудно видеть, что . Величина оценивается при помощи неравенства .

Остановимся теперь на некоторых свойствах знакопеременных рядов (т.е. знакочередующихся рядов и рядов с произвольным чередованием знаков своих членов).

Знакопеременный ряд сходится, если сходится ряд .

В этом случае исходный ряд называется абсолютно сходящимся.

Сходящийся ряд называется условно сходящимся, если ряд расходится.

Если ряд абсолютно сходится, то ряд, полученный после любой перестановки бесконечного множества его членов, абсолютно сходится и имеет ту же сумму, что и первоначальный ряд.

Если ряд условно сходится, то при перестановке бесконечного множества его членов сумма ряда может измениться. В частности, при соответствующей перестановке членов условно сходящегося ряда его можно превратить в расходящийся ряд.

1.1.Найти общий член ряда .

Решение. Последовательные числители образуют арифметическую прогрессии. 1,3,5,7,…; й член прогрессии находим по формуле Здесь , поэтому . Последовательные знаменатели образуют геометрическую прогрессии. -й член этой прогрессии . Следовательно, общий член ряда

1.2. Найти общий член ряда

Решение. Показатель степени каждого члена совпадает с номером этого члена, поэтому показатель степени го члена равен . Числители дробей 2/3,3/7,4/11,5/15,…образуют арифметическую прогрессию с первым членом 2 и разностью 1. Поэтому -й числитель равен . Знаменатели образуют арифметическую прогрессию с первым членом 3 и разностью 4. Следовательно, -й знаменатель равен . Итак, общим членом ряда является

1.3. Найти сумму ряда .

Решение. Разлагаем общий член ряда на простейшие дроби:

Выписываем несколько членов ряда так, чтобы было видно, какие слагаемые сокращаются при вычислении частичной суммы ряда:

.

Составляем ю частичную сумму ряда:

Вычисляем сумму ряда по формуле , получаем . Ряд сходится и его сумма равна 1/2.

1.4. Найти сумму ряда .

Решение. Разложим общий член ряда на простейшие дроби с помощью метода неопределенных коэффициентов:

.

Умножая на знаменатель левой части, придем к тождеству

Полагая последовательно находим:

при : 1=2A; A=1/2;

при :

при

Таким образом, , т.е.

.

Выписываем несколько членов ряда, чтобы было видно, какие слагаемые сокращаются при вычислении частичной суммы ряда:

.

Составляем ю частичную сумму ряда и сокращаем все слагаемые, какие возможно:

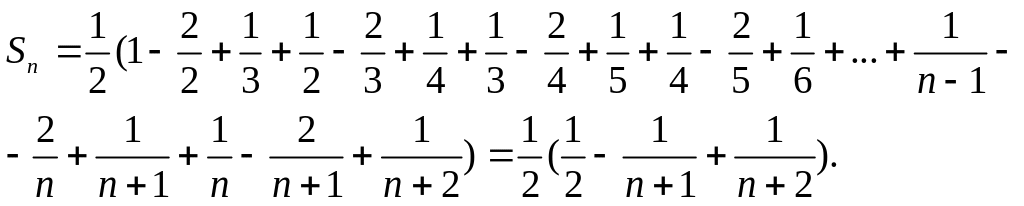
Вычисляем сумму ряда по формуле ,

получаем .

Ряд сходится и его сумма равна 1/4.

1.5. Исследовать сходимость ряда .

Решение. Ряд составлен из членов бесконечно убывающей геометрической прогрессии и поэтому сходится. Найдем сумму ряда. Здесь (знаменатель прогрессии). Сле-

довательно,

1.6. Исследовать сходимость ряда

.

Решение. Данный ряд получен из гармонического отбрасыванием первых десяти членов. Следовательно, он расходится.

1.7. Исследовать сходимость ряда .

Решение. Находим общий член ряда . Так как

, т.е. ,

то ряд расходится (не выполняется необходимое условие).

1.8. Исследовать сходимость ряда

Решение. Члены данного ряда меньше соответствующих членов ряда , т.е. ряда . Но последний ряд сходится как бесконечно убывающая геометрическая прогрессия. Следовательно, сходится и данный ряд.

1.9. Исследовать сходимость ряда

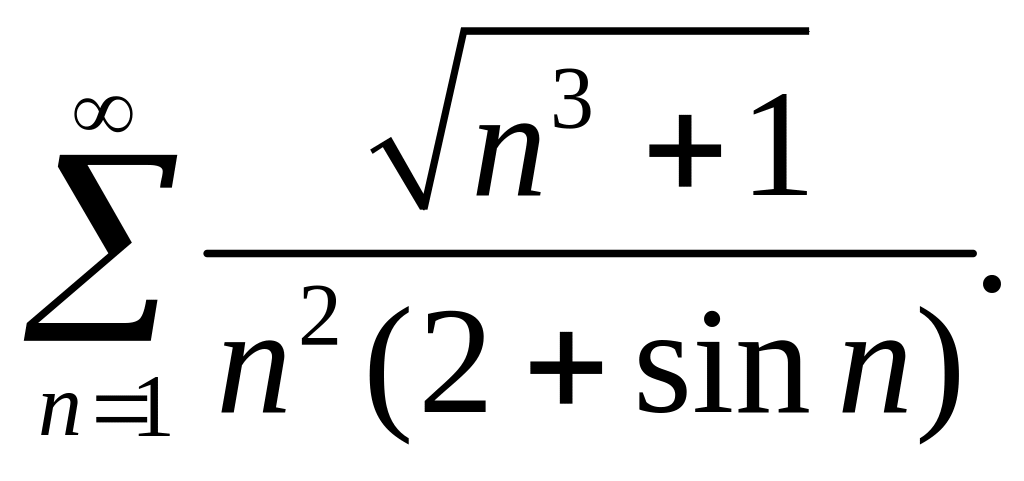
Решение. Так как , то необходимое условие сходимости ряда выполнено. Применим первый признак

сравнения. Поскольку , имеем

и, следовательно, 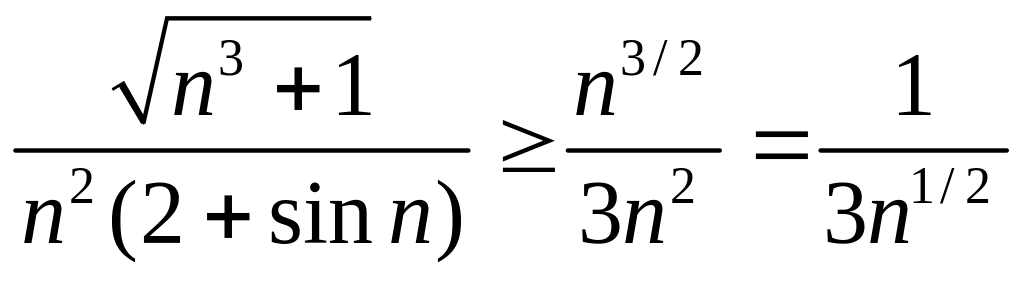. Так как ряд

расходится как обобщенный гармонический ряд с , то по первому признаку сравнения расходится и исходный ряд.

1.10. Исследовать сходимость ряда .

Решение. Здесь . Сравним ряд с гармоническим рядом, у которого : . Следовательно, данный ряд расходится по второму признаку сравнения.

1.11. Исследовать сходимость ряда

Решение. Так как , то необходимое условие сходимости ряда выполнено. Проверяем, что члены данного ряда положительны. Действительно, >0 при всех , так как . Имеем при Ряд сходится как обобщенный гармонический ряд с . Следовательно, в силу второго признака сравнения исходный ряд также сходится.

1.12.Исследовать сходимость ряда .

Решение. Применим признак Даламбера. Имеем

,

значит, Так как , то ряд расходится.

1.13.Исследовать сходимость ряда

Решение. Применим признак Даламбера. Имеем , поэтому

Следовательно, ряд сходится.

1.14. Исследовать сходимость ряда

Решение. Применим признак Коши. Здесь .

Вычисляем Так как , то ряд сходится.

1.15. Исследовать сходимость ряда

Решение. Применим признак Коши. Здесь . Поскольку, , то вычисляем

Так как , то ряд расходится.

1.16. Исследовать сходимость ряда

Решение. Поскольку при , упрощаем выражение для : т. е. будем исследовать сходимость ряда и затем воспользуемся вторым признаком сравнения. Поскольку , вычисляем , учитывая, что

: .

Так как , то ряд сходится. Следовательно, по второму признаку сравнения сходится и исходный ряд.

1.17. Исследовать сходимость ряда

Решение. Применим интегральный признак: ,

следовательно, , . Интеграл сходится

(является конечной величиной), поэтому сходится и данный ряд.

1.18. Исследовать сходимость ряда

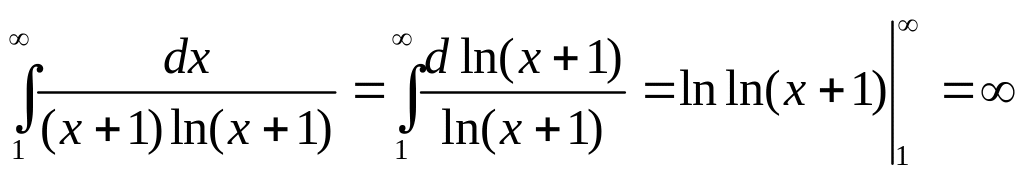Решение. Применим интегральный признак: , следовательно, , . Интеграл расходится, поэтому расходится и исходный ряд

1.19. Исследовать сходимость ряда

Решение. Упростим выражение для :

и будем исследовать сходимость ряда с помощью интегрального признака Коши. Ряд расходится так как

расходится интеграл

.

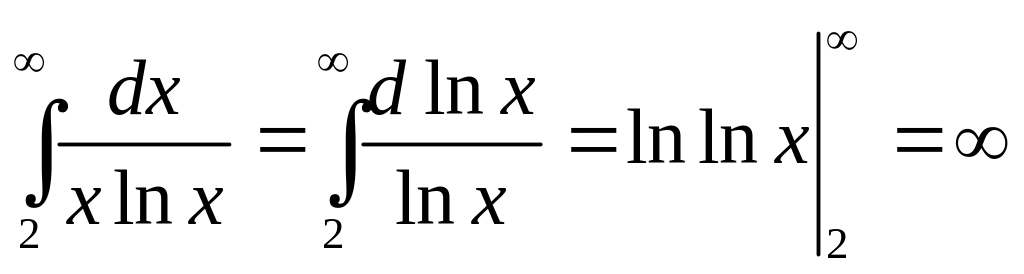Из расходимости ряда по второму признаку сравнения следует расходимость ряда

1.20. Исследовать сходимость знакочередующегося ряда

.

Решение. Составим ряд из абсолютных величин: . Применим второй признак сравнения: . Гармонический ряд расходится, поэтому по второму признаку сравнения расходится ряд , следовательно, ряд не является абсолютно сходящимся. Применим признак Лейбница. Так как , то выполнено первое условие признака Лейбница. Поскольку , имеем , т.е. выполнено второе условие. Ряд сходится условно.

1.21. Исследовать сходимость знакочередующегося ряда

.

Решение. Общий член ряда , поэтому . Следовательно, не выполнено

необходимое условие сходимости ряда. Ряд расходится.

1.22. Исследовать сходимость ряда

.

Решение. Составим ряд из абсолютных величин:

Этот ряд есть бесконечно убывающая геометрическая прогрессия и, следовательно, сходится. Значит, и данный ряд сходится, причем абсолютно.

1.23. Исследовать сходимость ряда .

Решение. Составим ряд из абсолютных величин:

. Так как при , то по вто-

рому признаку сравнения ряд из модулей расходится, следова-

тельно, ряд не является абсолютно сходящимся. Проверим выполнение условий признака Лейбница:

1) неравенство выполняется для любого

2) . Следовательно, по признаку Лейбница исходный ряд сходится условно.

1.24. Вычислить сумму ряда с точностью

Решение. Данный ряд знакочередующийся и сходящийся (абсолютно). Члены ряда убывают по абсолютной величине: , при любом . Следовательно, справедливо неравенство . Если , то и , поэтому решая неравенство , находим количество членов ряда, которое необходимо взять для вычисления суммы с заданной точностью . Получаем , т.е. достаточно взять первые три члена ряда. Вычисляем

Составить формулы общих членов рядов:

1.25. .

1.26 .

1.27. .

1.28. .

Ответы: 1.25. 1.26. 1.27. 1.28. .

Найти суммы рядов:

1.29. 1.30.

1.31. 1.32.

1.33. 1.34.

Ответы: 1.29. 1.30. 1.31. 1.32. 1.33. 1.34.

Исследовать сходимость рядов с помощью первого признака сравнения:

1.35. 1.36.

1.37. 1.38.

1.39. 1.40.

1.41. 1.42.

Ответы: 1.35.Ряд сходится. 1.36. Ряд сходится. 1.37. Ряд расходится. 1.38. Ряд сходится. 1.39. Ряд сходится. 1.40. Ряд расходится. 1.41.Ряд сходится. 1.42. Ряд расходится.

Исследовать сходимость рядов с помощью второго признака сравнения:

1.43. 1.44.

1.45. 1.46.

1.47. 1.48.

1.49. 1.50.

1.51.

Ответы: 1.43. Ряд сходится. 1.44. Ряд сходится. 1.45.Ряд сходится. 1.46.Ряд расходится. 1.47.Ряд сходится. 1.48. Ряд сходится. 1.49. Ряд сходится. 1.50.Ряд расходится. 1.51. Ряд сходится.

Исследовать сходимость рядов с помощью признака

Даламбера:

1.52. 1.53.

1.54. 1.55.

1.56. 1.57.

1.58.

Ответы. 1.52. Ряд сходится. 1.53. Ряд сходится. 1.54. Ряд сходится. 1.55. Ряд расходится. 1.56. Ряд сходится. 1.57. Ряд расходится. 1.58. Ряд расходится.

Исследовать сходимость рядов с помощью признака Коши:

1.59 . 1.60.

1.61. 1.62.

1.63. 1.64.

1.65. 1.66.

1.67. 1.68.

Ответы: 1.59. Ряд расходится ( ). 1.60. Ряд сходится

( . 1.61. Ряд сходится ( . 1.62. Ряд сходится ( . 1.63. Ряд сходится ( . 1.64. Ряд сходится ( . 1.65. Ряд сходится ( . 1.66. Ряд сходится ( . 1.67. Ряд сходится ( . 1.68. Ряд расходится ( .

Пользуясь интегральным признаком, исследовать сходимость рядов:

1.69. 1.70. 1.71.

1.72. 1.73.

При каких значениях параметра сходится ряд:

1.74.

Ответы:1.69. Ряд сходится. 1.70. Ряд расходится. 1.71.Ряд сходится. 1.72. Ряд сходится.1.73. Ряд расходится. 1.74. При ряд сходится, при ряд расходится.

Исследовать сходимость знакопеременных рядов и установить характер сходимости (абсолютная, условная):

1. 75 . 1.76.

1.77. 1.78.

1.79. 1.80.

1.81. 1.82.

1.83. 1. 84.

Ответы. 1.75. Ряд сходится условно.1. 76. Ряд сходится абсолютно.1. 77. Ряд сходится условно.1.78. Ряд сходится абсолютно.1.79. Ряд сходится условно. 1.80. Ряд сходится условно. 1.81. Ряд сходится абсолютно. 1.82. Ряд расходится. 1.83. Ряд сходится абсолютно.1.84. Ряд сходится условно.

Вычислить суммы знакочередующихся рядов с заданной точностью .

1.85. 1.86.

1.87. 1.88.

1.89. 1.90.

1.91. 1.92.

Ответы.1.85. 1.86. .1. 87.

1.88. 1.89. 1.90.

1.91. 1.92.