
Учебное пособие 800672
.pdf,- и вычисленными по уравнению регрессии Y на х значения-
ются , |
= 1,2,…, |
. Если модель адекватна, то остатки |
, явля- |
ми |
|
||
|
реализациями случайных ошибок наблюдений |
i= 1, 2, |
|
..., n, которые, в силу предположений, должны быть независимыми нормально распределенными случайными величинами с нулевыми средними и равными дисперсиями 2. Всякое отклонение от предложений относительно ошибок наблюдений е, должно отразиться на поведении остатков i=1, 2, ..., п. Различные графики остатков дают возможность определить те
или иные отклонения [4, 18]. |
|
|
|
, где S |
|||
|
График стандартизированных остатков |
|
|
||||
— оценка стандартного отклонения ошибок |
наблюдений в |
||||||
= |
/ |
|
|||||
функции |
предсказанного |
значения |
|
зависимой |
|||
ной |
, = 1,2,…, |
, позволяет обнаружить следующие дефекты |
|||||
|
|
||||||
регрессионной модели и исходных данных. |
|
|
|
||||
|
1) |
Наличие выбросов, т. е. таких остатков, |
которые по |
||||
абсолютному значению значительно превосходят все осталь-
ные остатки |
. Например такие остатки |
для которых |
| | > 3. |
|
|
2)Нарушение условия постоянства дисперсии ошибок для всех наблюдений. Если все остатки укладываются в симметричную относительно нулевой линии полосу, то дисперсии ошибок наблюдений можно считать постоянными.
3)Криволинейный характер графика остатков показывает, что в регрессионной модели не учтены факторы, оказывающие существенное влияние на зависимую переменную Y.
График стандартизированных остатков , в функции номера наблюдения i, i= 1, 2, ..., п, (что совпадает в некоторых задачах с графиком по времени) может показывать наличие корреляции между последовательными значениями или указывать на непостоянство дисперсии ошибок наблюдений (если остатки не укладываются в симметричную относительно нулевой линии полосу).
71

В случае если остатки на этом графике лежит в пределах полосы постоянной ширины, но имеют линейный или криволинейный тренд, то в регрессионную модель необходимо включить фактор, зависящий от номера наблюдения (или времени).
Если ошибки наблюдений i=1, 2, ..., п имеют нормальное распределение N(0, 2), то и остатки е, также должны иметь нормальное распределение. Гипотезу о нормальном распределении остатков при достаточно большом объеме выборки п можно проверить с помощью критерия или критерия Колмогорова—Смирнова. В статистических пакетах проверка выполнения этого условия обычно выполняется на специальном графике — вероятностной бумаге [14, 19]. Нормально распределенные остатки укладываются на прямую. Точки значительно удаленные от прямой можно рассматривать как выбросы. Если появление выбросов объясняется грубыми ошибками в исходных данных, то они должны быть исключены из дальнейшего анализа. В противном случае выбросы могут указывать на неадекватность модели.
Нарушение предположения о некоррелированности ошибок наблюдений i=1, 2, ..., п приводит к тому, что в последовательности остатков е, обнаруживается сериальная корреляция, т. е. корреляция между остатками i=1, 2, ..., п, отстоящими друг от друга на к шагов. Наличие сериальной корреляции в последовательности остатков проверяется с помощью критерия Дарбина—Уотсона.
Статистика критерия d вычисляется по формуле
( − )
=
Критерий Дарбина—Уотсона позволяет проверить гипотезу Н0: все сериальные корреляции равны 0, рк = 0, к = 1, 2,
... при альтернативной гипотезе : = , 0,| | < 1. Процедура проверки состоит в следующем. В зависимо-
сти от числа наблюдений п, числа оцениваемых параметров к
72
модели и уровня значимости по таблице (см. Приложение 2) находят два числа d1 и d2. В зависимости от формулировки альтернативной гипотезы , решение принимается по одному из следующих правил:
1): >0:
принимается, если d > d2, отклоняется, если d < d1,
при d1 d d2 решение не принимается;
2): <0:
принимается, если 4 - d > d2, отклоняется, если 4 - d < d{,
при 4 − решение не принимается;
|
3) : 0: |
|
|
принимается на уровне значимости 2 , если d > d2 |
|
или 4 |
- d > d2, |
|
или 4 |
отклоняется на уровне значимости 2 , если d < d1 |
|
- d < . |
|
|
|
Если гипотеза |
отклоняется, то либо ошибки наблю- |
дений в исходных данных коррелированны (в этом случае для оценки параметров нужно применять другие методы, например взвешенный метод наименьших квадратов [25]), либо в модели не учтен один или несколько существенных факторов, влияющих на зависимую переменную, либо неправильно выбрана форма связи между переменными.
Более тщательная проверка адекватности регрессионной модели может быть проведена, если для зависимой переменной Y проведены повторные наблюдения. В этом случае для проверки адекватности модели используется следующая
процедура дисперсионного анализа. |
|
|
|
||
Пусть при i-м значении фактора х, |
|
проведено |
, |
||
повторных наблюдений зависимой |
переменной Y,i= 1, 2, ..., т. |
||||
|
= |
, j= 1, 2, ..., |
|
||
Объем всей выборки |
.Обозначим |
|
„ |
||
наблюдений Y при i-м значении факто- |
|||||
результаты повторных = ∑ |
адекватна данным, то средние |
||||
ра х, = . Если модель |
73 |
|
|
|
|

= ∑ |
, = 1,2,…, |
|
|
|
должны быть близки к значениям |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
предсказанным регрессионной моделью |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Мерой |
неадекватности модели будет сумма квад- |
||||||||||||||
|
|
|
|
|
− |
= |
|
+ |
|
|
|
|
|
|
|||
ратов отклонений |
|
|
: |
|
|
|
|
|
|
. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
лучше результаты наблюдений со- |
|||||||||
|
|
Чем меньше Qn, тем= |
∑ |
|
|
|
− |
|
|
|
|||||||
гласуются с моделью. Возведя обе части тождества |
|||||||||||||||||
|
|
|
− |
= |
|
|
|
− |
|
+ |
|
− |
|
|
|||
|
|
|
|
|
|
|
|
|
|||||||||
в квадрат и просуммировав их по i и по j, получим, что остаточная сумма квадратов Qe может быть разбита на две суммы
и:
= ∑ ∑ |
− = ∑ |
|
− ̃ + ∑ ∑ |
− |
|
или
=+
Второе слагаемое Qp называется суммой квадратов чистой ошибки.
Если модель адекватна результатам наблюдений, то
статистики и независимы и имеют распределение со-
ответственно с (т - к) и (п- т) степенями свободы, где к — число оцениваемых параметров. Для простой линейной регрессии число оцениваемых параметров, к = 2.
В этом случае статистика |
−2) |
|
|
||||
|
|
/( |
|
|
|||
боды. |
|
/( |
− |
) |
|
|
|
имеет распределение |
Фишера с (т - 2) и (n - т) степенями сво- |
||||||
= |
|
|
|
|
|
|
|
Выборочное значение статистики F, FB сравнивается с |
|||||||
квантилью распределения Фишера |
|
|
( − 2, − ) |
. Если |
|||
в < ( −2, − |
), то гипотеза об |
|
|||||
|
|
|
|
|
|
адекватности модели |
|
|
|
|
74 |
|
|
|
|

принимается на уровне значимости . В противном случае модель не адекватна результатам наблюдений.
Если регрессионная модель значима и адекватна результатам наблюдений, то она может быть использована для определения прогноза ( ) при заданном значении независимой переменной х = х0.
Доверительный интервал для среднего значения Y при х=х0 определяется по формуле
|
|
|
|
|
|
|
|
1 |
|
( − |
|
) |
|
|
||
|
|
|
|
|
|
|
|
|
||||||||
а доверительный( интервал) |
( |
для−2)индивидуального+ |
значения Y |
|||||||||||||
при |
= |
вычисляется по формуле: |
|
|
||||||||||||
|
|
( ) |
( − 2) |
1+ |
1 |
+ |
( − |
|
) |
|||||||
|
|
|
||||||||||||||
где |
( |
) = + . |
|
|
|
|
|
|
|
|
|
|
|
|
||
Задачу регрессионного анализа удобно записывать в матричном виде. Введем следующие обозначения:
регрессионная матрица (n х 2)
1
= … … , вектор = … ,
1
вектор параметров модели = |
|
, |
||
|
||||
вектор ошибок наблюдений |
|
… . |
||
Тогда простая линейная |
регрессия |
определяется мат- |
||
|
= |
|
|
|
ричным уравнением
= +
Метод наименьших квадратов дает оценку , вычисляемую по формуле
75
= ( |
) |
, |
|
(2.43) |
||
где — матрица, транспонированная к матрице А; |
= В — |
|||||
информационная матрица; |
= ( |
) |
— матрица, обрат- |
|||
ная к матрице В = (АТА). |
|
|
||||
Сумма квадратов, обусловленная регрессией, определя- |
||||||
ется по формуле |
|
|
|
|
|
|
= |
− |
( |
|
) |
|
|
|
|
|
||||
Остаточная сумма квадратов: Qe =Qy -QR. Ковариационная матрица AT для оценок параметров
регрессии вычисляется по формуле
=( ) =
Дисперсии оценок параметров — диагональные элементы матрицы К:
= ( ),= ( )
где , =1,2 — диагональные элементы матрицы |
. |
2.4.4.Пример простой линейной регрессии Y на х
иего реализация в системе STATISTICA
Исходные данные: результаты наблюдений зависимой пе-
ременной (у) и фактора (х) следующие:
У |
X |
4,0 |
5,5 |
5,6 |
8,1 |
5,7 |
8,5 |
3,6 |
5,9 |
4,0 |
7,8 |
|
76 |

Решение.
1.По данным примера вычислим суммы квадратов Qy, Qx и сумму произведений Qxy; n=5. Предварительно найдем средние значения:
|
|
|
|
|
|
|
|
|
1 |
xi |
|
1 |
|
5,5 8,1 8,5 5,9 7,8 7,16 ; |
|||||||||||||||||||||||||
|
|
|
|
|
x |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
n |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
1 |
|
yi |
|
1 |
4 5,6 5,7 3,6 4 4,58; |
|||||||||||||||||||||||||||
|
|
|
|
y |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
x |
|
2 |
|
|
|
|
|
|
|
|
xi2 n |
|
2 |
5,52 |
8,12 8,52 5,92 7,82 5 7,16 2 |
||||||||||||||||||||||
Q |
|
|
|
|
|
|
|
x |
|||||||||||||||||||||||||||||||
x |
|
|
|||||||||||||||||||||||||||||||||||||
x |
|
i |
|
|
|
|
|
263,76 5*51,226 7,432; |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Qy |
yi |
|
|
2 |
yi2 n |
|
2 |
42 5,62 |
5,72 3,62 |
42 5* 4,582 |
|||||||||||||||||||||||||||||
y |
y |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
108,81 5*20,976 3,928; |
|
||||||||||||||||||||||
Q |
x |
|
y |
|
|
|
|
|
|
|
|
|
x y n* |
|
* |
|
(5,5*4 8,1*5,6 8,5*5,7 |
||||||||||||||||||||||
x |
y |
|
|
|
|
|
|
x |
y |
||||||||||||||||||||||||||||||
|
xy |
|
i |
|
|
|
|
|
|
|
i |
|
|
|
|
i |
i |
|
|
|
|
|
|
|
|
|
|||||||||||||
5,9*3,6 7,8*4) 5*7,16*4,58 168,25 5*7,16*4,58 4,289. |
|||||||||||||||||||||||||||||||||||||||
|
Оценки |
|
|
параметров линейной |
регрессии |
y 0 1x |
|||||||||||||||||||||||||||||||||
равны: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Qxy |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
4,289 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
0,577; |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Qx |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7,432 |
|
|||||||||||
~~
0 y 1*x 4,58 0,577*7,16 0,451.
Таким образом, уравнение линейной регрессии Y на х имеет вид
у =0,451 + 0,577*x.
Аналогично, оценки параметров линейной регрессии X
на у.
~ |
' |
|
Q |
xy |
~ ' |
|
|
~ ' |
|
|
|||
|
|
|
|
1,091; |
|
x |
|
y 7,16 1,091*4,58 2,163 |
|||||
1 |
Qy |
0 |
1 |
||||||||||
|
|
|
|
|
|
|
|
||||||
Уравнение линейной регрессии X на у имеет вид
х = 2,163 + l,091y 77
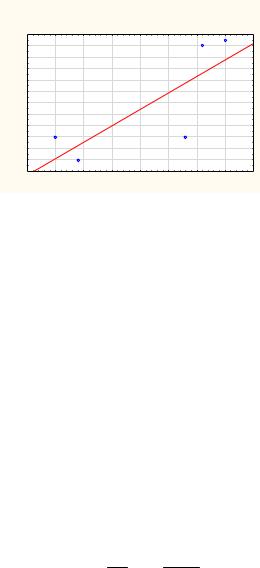
2. Диаграмма рассеяния исходных данных и прямая регрессии Y на х показана на рис. 2.13.
y
Scatterplot of y against x Spreadsheet1 10v*10c y = 0,4509+0,5767*x
5,8
5,6
5,4
5,2
5,0
4,8
4,6
4,4
4,2
4,0
3,8
3,6
3,4
5,0 |
5,5 |
6,0 |
6,5 |
7,0 |
7,5 |
8,0 |
8,5 |
9,0 |
|
|
|
|
x |
|
|
|
|
Рис. 2.13. Диаграмма рассеяния и прямая регрессии Y на х 3. Для линейной регрессии Y на х вычислим остатки:
ei |
yi |
|
~ |
~ |
|
|
0 |
1 |
xi ,i 1,2,...,5; |
||
|
|
|
|
|
|
e1 4 0,451 0,577*5,5 0,377; e2 5,6 0,451 0,577*8,1 0,478;
…………………………………………
e5 4 0,451 0,577*7,8 0,949.
Остаточная сумма квадратов Qe:
Qe = (0,377)2 + (0,478)2 + (0,35)2 + (-0,25)2 + (-0,949)2 1,457.
Оценка дисперсии ошибок наблюдений
S2 |
Qe |
|
1,457 |
0,486, |
|
n k |
5 2 |
||||
|
|
|
где k — число оцениваемых параметров; для простой линейной регрессии k 2.
Коэффициент детерминации R2:
R2 1 Qe 1 1,457 0,629. Qy 3,928
78

Оценка коэффициента корреляции r:
r |
|
Qxy |
|
|
|
4,286 |
|
0,793 |
|
|
|
|
|
|
|
||||
QxQy |
7,438*3,928 |
||||||||
|
|
|
|
|
|
|
4.Вычислим оценки параметров линейной регрессии Y на х
вматричном виде:
~ 1
AT A ATY,
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
; А — регрессионная матрица: |
|
|
|
|
|
||||||||||||||||
где |
~ |
0 |
|
|
|
|
|
|
||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
1 |
|
|
x |
|
|
|
1 |
5,5 |
|
|
|
y |
|
|
|
4 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
8,1 |
|
|
|
|
1 |
|
|
5,6 |
||
|
|
|
|
|
|
|
A |
1 |
|
|
x2 |
|
|
|
|
|
Y |
|
y2 |
|
|
|
||||
|
|
|
|
|
|
|
... |
... |
|
1 |
8,5 |
; |
|
... |
|
|
|
5,7 . |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
5,9 |
|
|
|
|
|
|
|
3,6 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
1 |
|
|
xn |
|
|
|
7,8 |
|
|
|
|
yn |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
Последовательно вычисляем: |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
T |
|
1 |
|
|
1 |
|
1 |
1 |
1 |
|
|
|
|
|
|
|
||||||
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
5,5 |
8,1 |
8,5 |
5,9 |
7,8 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
B |
AT A |
|
1 |
|
1 |
1 |
1 |
|
|
1 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
5,5 |
|
8,1 |
8,5 |
5,9 |
7,8 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
Определитель матрицы В: |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
= det(ATA)=37,6. |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
Обратная матрица к матрице В: |
|
|
|
|
|
|
|||||||||||||||||
|
B 1 |
1 |
*B* |
|
1 |
|
|
|
262,76 |
35,8 |
|
7,098 |
||||||||||||||
|
|
|
* |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
B |
|
|
37,16 |
|
|
|
|
|
|
|
5 |
|
|
|
0,963 |
|||||
|
|
|
|
|
|
|
|
|
|
35,8 |
|
|
|
|
|
|
||||||||||
0,963 0,135 ,
где B* — присоединенная матрица к матрице В, составленная из алгебраических дополнений к элементам матрицы В.
Далее вычисляем произведения матриц
79
B 1 *A 1 |
7,098 |
0,963 1 |
1 |
1 |
1 |
|
1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
0,963 |
|
5,5 8,1 |
8,5 |
5,9 |
7,8 |
|
|
||
|
|
0,135 |
|
|
|||||||
1,7992 |
|
0,7056 |
1,0910 |
1,4139 |
|
0,4166 |
|
|
|||
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
0,1265 |
0,1803 |
|
0,1695 |
0,0861 |
|
|
|
||
0,2234 |
|
|
|
|
|||||||
Окончательно
~ ~ 0 B 1ATY~
1
1,7992 |
0,7056 |
1,0910 |
1,4139 |
0,4166 |
|||
|
|
|
|
|
|
|
. |
|
0,2234 |
0,1265 |
|
0,1803 |
0,1695 |
0,0861 |
|
|
|
|
|||||
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5,6 |
|
0,4509 |
|
|
|
|
|
5,7 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
0,5767 |
|
|
|
||
|
|
3,6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
Сравнивая полученные значения с результатами в п. 2 видно, что расхождение имеется только в третьем десятичном знаке.
5. Выполнение задания в пакете STATISTICA. 5.1.Откройте новый файл данных. В таблице удалите
ненужные столбцы (Var-Delete) и строки наблюдений (CasesDelete). Дайте имена переменным: Y— зависимая переменная (Dependent), X— фактор (независимая переменная — Independent). В ячейки таблицы введите данные.
5.2.Построим график исходных данных. Для этого можно воспользоваться меню Graphs — графики и выбрать необходимый тип графика.
80
