Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Учебное пособие 800259

.pdf

Скачиваний:

Добавлен:

01.05.2022

Размер:

1.18 Mб

Скачать

☆

1 / 61 2 3 4 5 6 > Следующая >>>

ФГБОУ ВПО «Воронежский государственный технический университет»

Кафедра систем информационной безопасности

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к практическим занятиям по дисциплине «Теория радиотехнических сигналов»

для студентов специальности 090302 «Информационная безопасность телекоммуникационных систем» очной формы обучения

Воронеж 2014

Составитель д-р техн. наук Н. М. Тихомиров

УДК 004.056.5

Методические указания к практическим занятиям по дисциплине «Теория радиотехнических сигналов» для студентов специальности 090302 «Информационная безопасность телекоммуникационных систем» очной формы обучения / ФГБОУ ВПО «Воронежский государственный технический университет»; сост. Н. М. Тихомиров. Воронеж, 2013. 56 с.

Методические указания посвящены исследованию аналоговых и дискретных сигналов, их воздействию на линейные и нелинейные цепи, а также способов фильтрации от помех.

Методические указания подготовлены в электронном виде в текстовом редакторе MS Word 2013 и содержатся в файле Тихомиров _ПЗ_ТРС.docx.

Ил. 13. Библиогр.: 5 назв.

Рецензент д-р техн. наук, проф. А. Г. Остапенко

Ответственный за выпуск зав. кафедрой д-р техн. наук, проф. А. Г. Остапенко

Издается по решению редакционно-издательского совета Воронежского государственного технического университета

Практическая работа № 1 Случайные процессы. Законы распределения

и моментные функции

Целью практической работы является изучение основных свойств случайных процессов, определение и виды моментных функций.

Задачи практической работы:

дать определение случайному процессу;

рассмотреть основные характеристики закона распределения;

изучить виды моментных функций.

Теоретические сведения

Случайным процессом, сигналом Х(t) называется функция, значения которой в любой момент времени t – случайные величины. Фиксируя на определенном промежутке времени мгновенные значения случайного сигнала, мы получаем реализацию случайного процесса. Совокупность таких реализаций {

x1 (t) ,

x	2

(t)

x	3	(t)
	3

, …

x	k

(t)

…} образуется статистический

ансамбль, ансамбль реализации. Случайные процессы, реализации которых зависят от конечного числа случайных пара-

метров, называют квазидетерменированными.
	Совокупность получаемых в отдельных реализациях
величин		{ xk t1 },		K (1; ) , образует одномерное			сечение
данного случайного процесса. Плотность вероятности							p1 x, t1
случайной величины					X t1	называется одномерной	плотно-
стью вероятности процесса						X t в момент времени t1 . Величи-
на	dP p		x,t dx		есть вероятность того, что реализации
		1	1

случайного лежащие в

процесса в момент времени	t	1	примут значения,

интервале x; x dx . В общем случае n-мерное

сечение случайного процесса приводит к n-мерной плотности

вероятности

p	n	x	, x	2	,..., x	n	;t	,t	2	,...,t	n
	n	1		2		n	1		2		n

, которая должна удо-

влетворять следующим условиям:

1)положительной определенности;

2)нормировки;

3)симметрии: плотность вероятности не должна ме-

няться при любой перестановке своих аргументов

4) согласованности: при любом	m n

x	, x	2	,...,
1		2

x	n

;

, x

,..., x

,...,t

...

, x

,..., x

,...,t

...dx .

m 1

Характеристическая функция связана с соответствующей плотностью преобразования Фурье:

-одномерная характеристическая функция:

1	j, t	1	x, t exp{ j x}dx M exp j x
1		1
		p

(1)

- n-мерная характеристическая функция:

, j

,..., j

j x

... j

,...,t

exp

1 1

2 2

где

M - оператор математического ожидания.

(2)

Для характеристических функций так же справедливо условие симметрии, а условия нормировки и согласованности принимает вид:

n 0,0,...,0;t1 , t2 ,..., tn 1;

m j 1 , j 2 ,.... j m ;t1 ,t2 ...tm j 1 , j 2 ,.... j m ,0,0,...,0;t1 ,t2 ,...tn .

Моменты функций случайных процессов. Начальные моментные функции:

одномерная начальная моментная функция k-ого порядка – это математическое ожидание k-й степени

случайной величины

X (t)

t M X

p x,t dx;

(3)

мерная начальная моментная функция 1-ого порядка

, t

,...t

M X

...X

k k

...k

p x

dx ...dx

...

...x

, x

,..., x

, t

,...t

(4)

При

K K

.... K

n .

Одномерная начальная моментная функция первого по-

рядка

m1 t M X t xp1 x,t dx mx t

(5)

Называется математическим ожиданием, или средним

значением случайного

процесса

Широко

используется

так же двумерная начальная моментная функция второго порядка:


m1,1 t1, t2 M X t1 X t2	x1x2 p x1, x2 ; t1t2	dx1dx2
			(6)
Bx t1, t2 ,

называемая ковариационной функцией случайного процесса

x t .

Часто рассматривают n-мерные центральные моментные функции k-ого порядка:

k k

...k

,...,t

1 2

X t

M X t

= M

.... X

m			t
		x
K	n	t
	n
				n

				...
	K
			2
2


			k
		,	k

X t			m			t
								K
								n
		n			n		n
k	k			2	... k			n
1				2				n

(7)


где	X t X t mX			t - центрированный случайный процесс;
		X ti	mX ti - центрированная случайная величина.
X ti

Двумерная центральная моментная функция второго порядка

M	1,1	t	,t	2
	1,1	1		2

называется

X t .
	При
сией	D t ;

M X t

X t

(8)

корреляционной

функцией

случайного

процесса

t1 t2 t

функция

1,1

называется диспер-

D t K		t,t B		t,t m		t M X t m	t
					2		2	,
	X		X		X	x		,

которая позволяет определить средне квадратичное отклонение случайного процесса X t :

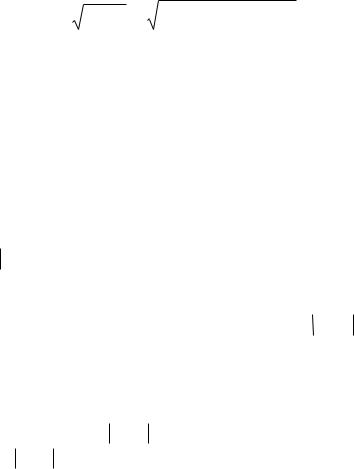
	t	D		t	M X t m		t
							2
X			X			X

стационарные случайные процессы.

Случайный процесс стационарен в узком смысле, если


любая его	-мерная плотность вероятности инвариантна отно-

сительно временного сдвига		:

p x	,...., x	n	;t	,..., t	n
1		n	1		n

p x	,...., x	n	;t	,..., t	n
1		n	1		n

Если же ограничить требования тем, что бы математическое ожидание и дисперсия процесса не зависели от времени, а функция автокорреляции определялась только разностью

t	2	t

		1

, т.е.

K	X	t	, t
	X	1	2

K	X

, то подобный процесс назы-

вают стационарным в широком смысле. Это эквивалент тому, что одномерная плотность вероятности процесса не зависит от

времени,						а
p x	, x	2	;t	,t	2
1		2	1		2

двумерная

x1 , x2 ; . Из

зависит	от	t	2	t	;
				1

определения стационарности

следуют свойства корреляционной и ковариационной функции:

; K

0 m

; B

(11)

Иногда используют нормированную функцию автокорреляции, называемую также коэффициентом корреляции случайного процесса:

R	K		/	2	; R	0 1
				2
x		x		x	x

(12)

Для нормального - гауссовского - случайного процесса оба понятия стационарности совпадают. В общем же случае

процесс, стационарный в узком смысле, стационарен и в широком смысле, но не наоборот.

Важный класс стационарных процессов - эргодические случайные процессы, любая статистическая характеристика которых, полученная усреднением по времени одной реализации, эквивалентна характеристике, полученной усреднением по ансамблю реализаций. Из этого определения следует:

m			lim		1		T x t dt
m		x	lim				T x t dt
		x	T T
			T T
						0
	lim					1		T
Bx						1		x t x t	dt
Bx								x t x t	dt
			T T					0
								0
				1		T
K x	l im			1		x t mx x t mx dt
K x	l im					x t mx x t mx dt
			T T			0
						0

(13)

(14)

(15)


	Решение. Случайная величина				x x t		при любом
	Найти одномерную плотность распределения вероятно-
стей процесса				x t cos t sin t - постоянная угловая ча-
стота; и				- взаимно независимые гауссовские случайные
величины			с	нулевыми математическими			ожиданиями
m	m	0	и равными дисперсиями		D	D		2	. Опреде-

лить, стационарный ли это процесс в широком или узком смысле.

фиксированном значении t представляет собой линейную комбинацию гауccовских случайных величин и в силу этого также


является гауссовской. Таким образом, для определения плот-
ности вероятности	p	x,t	и стационарности процесса необхо-
ности вероятности	1		и стационарности процесса необхо-
димо определить его математическое ожидание				m	x	t	и корре-
димо определить его математическое ожидание					x		и корре-
ляционную функцию K x t1 ,t2 .

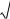
По определению для произвольного фиксированного момента времени t получаем:

x t

cos t sin t

cos t M

sin t.

Поскольку

по

условию

M m

;

M m

то mx

0 – математическое ожидание не зависит от времени;

M x t x t

M cos t1 sin t1 cos t2 sin t2

M 2 cos t1 cos t2 M 2 sin t1 sin t2

M cos t1 sin t2 cos t2 sin t1

Для гауссовских случайных величин независимость и
некоррелированность эквивалентны,					поэтому M 0	, то-
гда при условии M	2	M	2	2	получаем:

K		t	,t			2	cos t	cos t		sin t	sin t			2	cos t				t	K
						2								2
	x	1		2			1		2	1			2					2	1		x
					Таким образом, дисперсия							Dx K x 0				2	не зависит от
					Таким образом, дисперсия							Dx K x 0					не зависит от

времени, а автокорреляционная функция зависит только от

t	2	t	. Следовательно, процесс X(t) стационарен в широ-

		1

ким и в узком смысле.

Плотность вероятности рассматриваемого процесса не зависит от времени

p x	1		x	2
	1	exp	x
		exp			2
1	2		2		2	.
	2		2

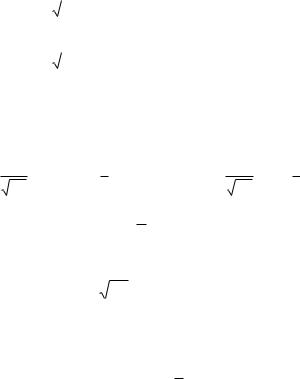
Определить одномерную характеристическую функцию нормального стационарного случайного процесса X(t), имею-

щего математическое ожидание				m		и дисперсию		2	.
Решение. По определению (I)

1 j M e j x p x e j x dx

	1		x m 2
		exp		2	2		exp j x dx

	2
	2
	1		x m 2
		exp		2	2		j x dx

	2
	2
Вводя замену		переменной				y x m /		и дополняя

показатель степени экспоненты до полного квадрата, получим:

	j	1					1	y2								1				1
		1	e j m	exp			1							dy		1				1	v2 2
			e j m	exp						2 j y				dy			exp				v2 2	j m
1		2					2									2				2
		2					2									2				2

									1						2
									1						2
						exp					y j					dy .
									2



	Поскольку				1/			2		exp t		2	/ 2 dt 1					,	то	искомая			ха-
	Поскольку				1/			2		exp t			/ 2 dt 1					,	то	искомая			ха-

рактеристическая функция нормального случайного процесса:

		1	2	2
	j exp
1		2
		2

1 / 61 2 3 4 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.05.20221.16 Mб7Учебное пособие 800254.pdf
#
01.05.20221.16 Mб6Учебное пособие 800255.pdf
#
01.05.20221.17 Mб5Учебное пособие 800256.pdf
#
01.05.20221.18 Mб2Учебное пособие 800257.pdf
#
01.05.20221.18 Mб3Учебное пособие 800258.pdf
#
01.05.20221.18 Mб3Учебное пособие 800259.pdf
#
01.05.2022298.3 Кб2Учебное пособие 80026.pdf
#
01.05.20221.19 Mб5Учебное пособие 800260.pdf
#
01.05.20221.19 Mб11Учебное пособие 800261.pdf
#
01.05.20221.19 Mб1Учебное пособие 800262.pdf
#
01.05.20221.2 Mб27Учебное пособие 800263.pdf