
Учебное пособие 800118
.pdf
Содержание отчета
1.Название и цель работы, краткие теоретические сведения о методе Ньютона.
2.Заданная функция, ее первая и вторая производные.
3.Блок-система алгоритма.
4."Листинг" программы и результаты ее выполнения.
5.Результат выполнения программы построения кривой заданной функции и сравнение полученных данных со значениями, полученными с помощью любого стандартного программного обеспечения.
6.Выводы по работе.
Контрольные вопросы
1.Поясните порядок поиска точки экстремума функции методом Ньютона.
2.Ни каких соображений выбирается значение начальной точки для аппроксимации корня?
3.По какому выражению ищется каждое последующее значение аппроксимируемого корня?
Таблица 2.1
Варианты задания для лабораторной работы № 1
№ |
Функция |
№ |
Функция |
|
варианта |
варианта |
|||
|
|
1 |
x2 |
|
−Sinx |
15 |
e−x −Cosx |
||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
x 2 |
−Cosx |
16 |
ex + Cosx |
|||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
x 2 |
− 4Sinx |
17 |
e−x −Sin2x |
|||||||||||||
4 |
3x + 4tgx |
18 |
e−x −Sinx |
||||||||||||||
5 |
x + Cosx |
19 |
ex +Sinx |
||||||||||||||
6 |
4x2 + Cosx |
20 |
ex + 4Cos2x |
||||||||||||||
7 |
x2 |
|
+ Sinx |
21 |
e−x Sinx |
||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||
8 |
0,85x0,5 + 0,3tgx |
22 |
|
|
x ex |
||||||||||||
9 |
x(x −1)2 |
23 |
x2 + ex Sinx |
||||||||||||||
10 |
|
|
|
|
x |
|
24 |
|
tgx + ex |
||||||||
|
|
x2 +1 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
11 |
|
|
|
|
x |
|
25 |
tg(−x)+ |
1 |
|
|||||||
|
(x +1)2 |
|
|||||||||||||||
|
x2 |
||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||
12 |
x2 (x −1) |
26 |
|
|
tgx |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2x2 |
||||
13 |
|
|
|
|
|
|
|
|
|
27 |
|
Sin2x |
|||||
|
|
|
|
x +1 |
|||||||||||||
|
|
|
|
|
|
|
x |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
14 |
x |
|
|
|
|
|
|
28 |
|
|
+ Cosx |
||||||
|
x2 +1 |
|
|
x |
|||||||||||||
11
12
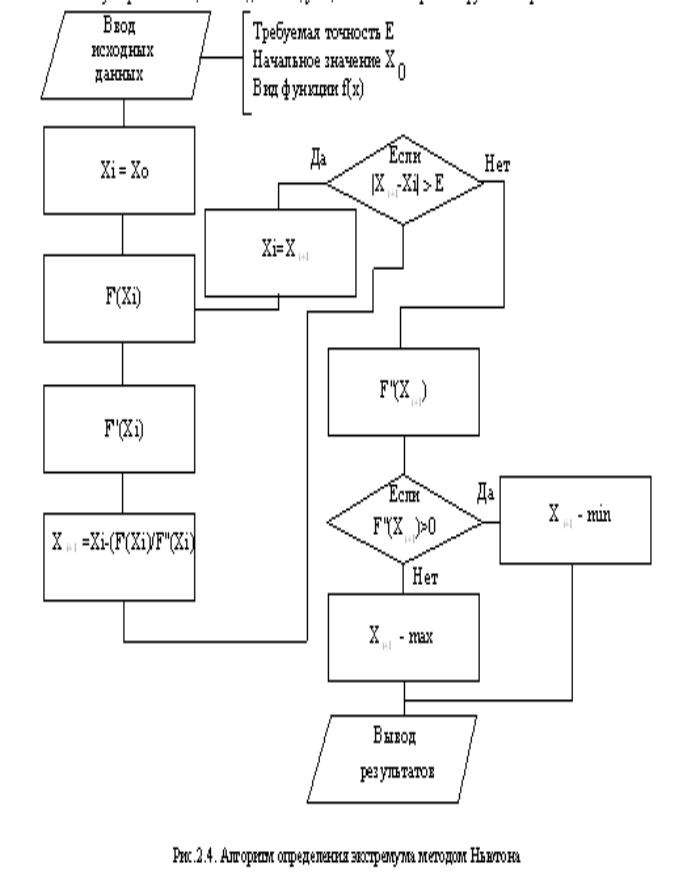
ПРАКТИЧЕСКИЕ РАБОТЫ № 2 - 3 ПОИСК ОПТИМУМА МЕТОДОМ ФИБОНАЧЧИ
И «ЗОЛОТОГО СЕЧЕНИЯ»
Цель работы: теоретическое изучение и получение практических навыков отыскания оптимума функции методом Фибоначчи.
Теоретические сведения
Часто существуют задачи, которые не дают возможности определить экстремум функции классическими методами. Это может быть пример, когда решить уравнение и найти его корни традиционным способом не удается. В этом случае с помощью численных методов экстремум функции f(x) ищется непосредственно в некотором интервале a < x0 < b, в котором как предполагается лежит экстремум.
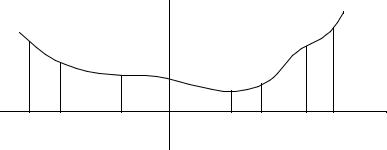
Пусть точки а и в определяют интервал, в котором лежит истинная точка минимума и внутри этого интервала функция унимодальная, т.е. имеет только один экстремум (рис. 3.1). В интервале [а, b] известны значения функции в трех
точках x1, x2, x3, таких что a < x1 < x2 < x3 < b, f(x2) < f(x1), f(x2) < f(x3).
Тогда точка xm лежит внутри интервала (x1, x3), меньшем чем (а, b). Внутри отрезка (x1, x3) мы можем вычислить функцию в точке x4, но сде-
лать это только один раз. При этом точка x4 помещается внутри отрезка (x1, x3) симметрично точке x2, т.е. длины (x1, x2) и ( x4, x3) должны быть одинаковы. После этого следует переходить к рассмотрению отрезка (x1, x2) или (x4, х3), которые меньше начального интервала (x1, x3) а точка экстремума лежит заведомо внутри этих интервалов.
Координата точки x2 при известном начальном интервале (x1; x3) определяется по выражению:
x 2 |
= |
Fn−1 [x3 |
−x1 ]+ |
(−1)n ε ; |
(3.1) |
|
|
Fn |
|
Fn |
|
|
|
|
Y |
|
|
|
a |
X1 |
X 4 |
Xm |
X 2 |
X 3 |
b X |
Рис. 3.1. Поиск экстремума функции методом Фибоначчи
13

где n - количество вычислений, которые необходимо выполнить;
ε - минимально возможное расстояние между двумя точками, возможно ε
= 0;
Fn-1 |
Fn , Fn-1 - числа Фибоначчи, которые определяются как: F0 = 1, F1 = 1, Fn = |
||||||||||||||||||||||||||
+ Fn-2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Последующее определение координаты точки x4 в числах Фибоначчи не |
||||||||||||||||||||||||||
нуждается и осуществляется по выражению: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
x 4 |
= x1 |
− x 2 + x3 |
|
|
|
(3.2) |
||||||||||||
|
Обозначим f(x2) = Y2 и f(x4) = Y4 |
и рассмотрим 4 возможных варианта |
|||||||||||||||||||||||||
взаимного расположения точек x2, x4 |
и значений функций Y2, Y4 (рис.3.2). |
||||||||||||||||||||||||||
|
|
|
|
Y4 |
2 |
|
|
|
|
|
|
|
|
|
Y |
|
Y |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
а) |
|
|
|
|
|
|
|
|
|
|
б) |
|
2 |
|
4 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
X |
1 X |
4 X |
2 X3 |
|
|
X1 X 2 |
X4 X3 |
||||||||||||||||||
|
|
|
|
X4 |
< |
X2 |
|
|
|
|
X2 |
< |
|
X4 |
|||||||||||||
|
|
|
|
Y4 |
< |
Y2 |
|
|
|
|
Y4 |
< |
|
Y2 |
|||||||||||||
|
в) |
|
|
Y4 |
Y2 |
|
|
|
г) |
|
|
|
Y2 |
|
Y4 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
X1 X4 X2 X3 |
|
|
|
|
|
X1 X2 X4 X3 |
|||||||||||||||||||
|
|
|
|
X4 |
< |
X2 |
|
|
|
|
|
|
X2 |
|
< |
X4 |
|||||||||||
|
|
|
|
Y2 |
< |
Y4 |
|
|
|
|
|
|
Y2 |
|
< |
Y4 |
|||||||||||
Рис. 3.2. Возможные варианты выбора значения координат точек и значений функций
Проанализировав рис. 3.2 можно сделать вывод о том как происходит выбор интервалов для последующих итераций. Для ситуации (рис. 3.2. а) выбираем новый интервал (x1, x2), содержащий точку x4. Для (рис. 3.2 б) выбираем интервал (x2, x3), содержащий точку x4. Для рис. 3.2 в выбираем новый интервал (x4,x3), содержащий точку x2, а для рис. 3.2 г выбираем интервал (x1, x4) содержащий точку x2.
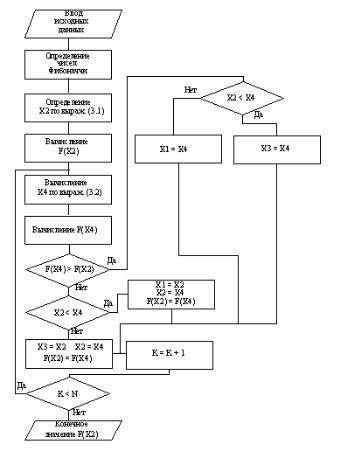
Процесс выбора оптимального, в случае поиска минимума, значения функции методом Фибоначчи может быть реализован в соответствии с алгоритмом, изображенном на рис. 3.3.
Частным случаем метода Фибоначчи является метод “золотого сечения”, особенностью которого является то, что не нужно знать количество вычислений функции “n”. При этом принимают отношения интервалов постоянным:
Lj−1 |
= |
Lj |
= |
Lj+1 |
= ... = τ, |
(3.3) |
|
Lj+1 |
Lj+2 |
||||
Lj |
|
|
|
|||
где Lj - длина отрезка, полученного при j-ом делении;
14
τ - постоянная, характеризующая “золотое сечение”, τ = 1,618033989.
Рис. 3.3. Алгоритм поиска оптимума методом Фибоначчи |
|
|||
При таком делении исходного отрезка (x0, x3) (рис. 3.4) на три участка |
||||
две последующие точки x1 и x2 вычисляются по выражению: |
|
|||
x1 |
= x0 |
+ t1 (x3 |
− x0 ), |
(3.4) |
x 2 |
= x0 |
+ t 2 (x3 |
− x0 ), |
(3.5) |
где t1, t2 - коэффициенты “золотого сечения”, соответственно равные: |
|
|||
|
t1 = 2 - τ |
|
(3.6) |
|
t2 = 1 - t1 = 1 - 2 + τ = -1 + τ |
(3.7) |
|||
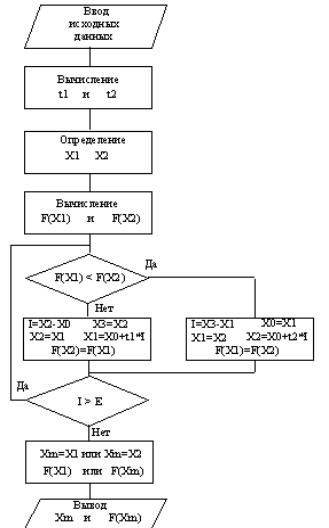
Алгоритм поиска минимума функции методом "золотого сечения" представлен на рис. 3.5.
15

F(X0) |
|
F(X2) F(X3) |
F(X0) |
|
|
|
F(X3) |
|||||||||||||||
|
|
F(X1) |
|
|
|
|
|
|
|
|
F(X1) |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F(X2) |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
0 |
X |
|
X |
2 |
X |
3 |
|
|
X0 |
X1 |
X |
2 |
X |
|||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
б) |
3 |
||||||
|
|
|
|
а) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рис. 3.4. Варианты деления начального отрезка (x0, x3) на три части: а) при следующих вычислениях переходим к
отрезку (x1; x3);
б) при последующих вычислениях к отрезку (x0; x2).
Порядок выполнения работы
1.Заданием на работу является выражение, исследование которого студент проводил при выполнении лабораторной работы № 1. Используя точки экстремума, определенные ранее, необходимо выбрать интервал, на котором будет осуществляться поиск точки минимума функции.
2.Опираясь на теоретические сведения и алгоритм, приведенный на рис.
3.3.разрабатывается программа вычисления точки экстремума функции методом Фибоначчи. Программа после проверки ее работы прикладывается к отчету. По результатам вычислений точек минимума заполняется табл. 3.1.
Таблица 3.1
Результаты определения экстремума функции
|
|
Количе- |
Минималь- |
ме- |
метод |
|
Точка |
|
но возмож- |
тод |
“золо- |
|
|
мини- |
№ вычис- |
ство при- |
ное рассто- |
Фиб |
того |
метод |
мума |
ле-ния |
ближений |
яние между |
она- |
сече- |
Ньютона |
|
|
N |
точками ε |
ччи |
ния” |
|
|
|
|
|
|||
|
1 |
30 |
0 |
|
|
|
1 |
2 |
100 |
|
|
|
|
|
|
|
|
|||
3 |
30 |
0,005 |
|
|
|
|
|
|
|
|
|||
|
4 |
100 |
|
|
|
|
|
|
|
|
|
||
|
5 |
30 |
0 |
|
|
|
2 |
6 |
100 |
|
|
|
|
|
|
|
|
|||
7 |
30 |
0,005 |
|
|
|
|
|
|
|
|
|||
|
8 |
100 |
|
|
|
|
|
|
|
|
|
||
. . . . |
|
|
|
|
|
|
N |
|
|
|
|
|
|
16
3. Аналогичная работа проделывается для метода “золотого сечения”, при чем вычисления по этому методу производятся с различной точностью, а результаты расчета распечатываются и сводятся в табл. 3.1.
Содержание отчета
1.Название и цель работы, краткие теоретические сведения по методу "Фибоначчи" и "золотого сечения".
2.Заданная функция и алгоритм. Определение точки минимума методом Фибоначчи и методом “золотого сечения”.
3.Распечатку программ и результатов выполнения, а также заполненную таблицу 3.1.
4.Алгоритм поиска точки максимума функции, распечатку программы реализующую процедуру поиска, результаты и заполненную табл. 3.1.
5.Выводы по работе.
Рис. 3.5. Алгоритм решения задачи по методу «золотого сечения»
17
Контрольные вопросы
1.Для каких случаев целесообразно применение метода Фибоначчи?
2.Поясните порядок деления отрезка с использованием числа Фибоначчи.
3.Какие варианты могут возникнуть при выборе четвертой точки в отрезке?
4.Запишите выражения для определения чисел Фибоначчи и точки при поиске точки максимума функции методом Фибоначчи.
5.В чем сходство и в чем отличие поиска оптимума функции методами Фибоначчи и “золотого сечения”?
ЛАБОРАТОРНАЯ РАБОТА № 2 ЭТАПЫ МОДЕЛИРОВАНИЯ
Цель работы: теоретическое изучение основных этапов моделирования, классификации моделей и получение практических навыков создания моделей различных видов.
Теоретические сведения
При исследовании любой системы посредством математического моделирования возможно наличие многих альтернативных вариантов моделей. Каждая из них в чем -то лучше остальных, а чем-то хуже. Поэтому процесс разработки наилучшего, как правило, компромиссного варианта модели, достаточно сложен. Системный подход предполагает наличие следующих этапов создания модели.
1. Синтез модели – создание возможных ее вариантов. Различают
а) структурный синтез – разработка структуры модели: ее общего вида (например, в виде многочлена, или другой функции), определение числа параметров и т. п.
б) параметрический синтез – поиск числовых значений параметров модели либо на основании справочных данных, либо исходя из условия максимального совпадения результатов, найденных по модели, с экспериментальными.
2.Анализ модели – определение качества синтезированного варианта по критериям:
а) универсальности – полноты отображаемых свойств объекта; б) точности – степени совпадения реальных данных с предсказанными
моделью; в) адекватности – способности правильно отображать свойства объекта;
г) экономичности – затрат на разработку и реализацию модели.
3.Выбор и принятие решений – общая оценка полезности вариантов и выбор лучшего.
18
В процессе перехода от словесного описания к получению результатов исследования модель объекта претерпевает следующие изменения формы своего представления.
Аналитическая модель описания – описание свойств объекта в виде совокупности математических зависимостей.
Модель решения – система математического моделирования соотношений, позволяющих найти решение поставленной задачи. Существует несколько альтернативных типов этой модели:
а) аналитическая модель решения – явное выражение, позволяющее вычислить искомую величину;
б) численная модель – запись решения в виде численных схем, позволяющих найти решение в виде набора чисел;
в) имитационная модель – переложение ан язык ЭВМ набора формальных правил функционирования объекта исследования при заданном входном воздействии.
3.Алгоритмическая модель – реализация модели решения в виде ал-
горитма.
4.Программная модель – реализация алгоритмической модели на языке программирования.
Если при разработке какой-либо из перечисленных форм возникают альтернативные варианты моделей, то появляется необходимость в реализации процедур синтеза, анализа, принятия решения.
Пример задачи моделирования
В качестве примера разберем следующую задачу. Необходимо спроектировать емкость заданного объема V0 оптимальных размеров: r – радиуса основания и h – высоты, имеющую форму прямого цилиндра с кромкой по периметру верхнего основания заданной высоты h0. В качестве критериев оптимальности можно выбрать любой из параметров (или оба одновременно):
S = Sбок + 2Sосн – площадь поверхности емкости;
L = 2Lосн + (h +h0) – длина сварного шва.
Т. к. на поверхность затрачивается листовой материал, а при сваривании расходуется электроэнергия, электроды и т. д., то в целях экономии значения обоих критериев должны быть минимальны. Кроме того, станок на котором будет реализован заказ, позволяет вырезать днище ограниченного радиуса:
R1 <r<R2.
Основные этапы решения задачи
1)Составление аналитической модели описания. Обозначим Q-
выбранный критерий оптимальности (S или L). Возможны два варианта структуры модели.
19
а) Двухпараметрическая |
|
Q(r, h) →min, |
(5.1) |
V(r, h) = 0, |
(5.2) |
R1 <r<R2. |
(5.3) |
Необходимо учитывать условный минимум функции двух переменных. б) однопараметрическая
h = h(r,V0), |
(5.4) |
подставим в (1) получим |
|
Q(r, h(r, V0)) →min. |
(5.5) |
Требуется найти минимум функции одной переменной на отрезке. |
|
Проверим анализ каждого варианта. Очевидно, что вторая модель лучше с позиций критерия экономичности, если существует аналитическое решение уравнения (5.2) в виде (5.4). В этом случае выбрать надо модель описания (б), т. к. по остальным критериям обе модели эквивалентны. В противном случае надо остановиться на модели (а). В предлагаемой задаче решение (4) существует, поэтому в дальнейшем рассматривается однопараметрическая модель. Для параметрического синтеза модели описания надо в выражения (3) – (5) при конкретном критерии оптимальности подставлять указанные в вариантах задания
значения V0, h0, R1, R2. |
|
|
2) Разработка модели принятия решения. Минимум функции, как из- |
||
вестно, достигается в стационарной точке, т. е. где |
|
|
∂Q(r) = 0 |
. |
(5.6) |
∂r |
|
|
Возможны следующие варианты:
1)Стационарная точка принадлежит интервалу [R1, R2] и аналитическое решение уравнения (5.6) существует. В этом случае необходимо применять аналитическую модель решения, т. к. с точки зрения точности и экономичности она лучше.
2)Стационарная точка принадлежит интервалу [R1, R2] и аналитического решения уравнения (5.6) не существует, или не приемлемо с позиции критерия экономичности. В этом случае необходимо применять численную модель решения.
3)Стационарная точка не принадлежит интервалу [R1, R2]. Это означает, что как аналитическая, так и численная модели, основанные на уравнении (5.6), не адекватны объекту моделирования и необходима имитационная модель.
Таким образом, для выбора модели решения необходимо проверить выполнение условия (5.3). Это можно сделать с помощью леммы БольцманаКоши: если
∂Q |
|
& |
∂Q |
|
>0 |
, |
(5.7) |
|
|
<0 |
|
||||||
∂r |
|
r=R1 |
|
∂r |
|
r=R 2 |
|
|
|
|
|
|
|
||||
то на отрезке (5.3) есть хотя бы одна стационарная точка. Для проверки отношения (5.7) надо найти производную ∂Q/∂R , вычислить ее значение при
20
