
Методы и модели в расчетах на ЭВМ. методические указания к выполнению лабораторных и практических работ для студентов. Перова А.В
.pdfМИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Воронежский государственный технический университет»
Кафедра технологии машиностроения
МЕТОДЫ И МОДЕЛИ В РАСЧЕТАХ НА ЭВМ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к выполнению лабораторных и практических работ для студентов направления 15.03.05 «Конструкторско-технологическое обеспечение машиностроительных производств»
(профили «Конструкторско-технологическое обеспечение кузнечно-штамповочного производства», «Металлообрабатывающие станки и комплексы», «Технология машиностроения»)
всех форм обучения
Воронеж 2021
УДК 51:621(075.8) ББК 22.1:34.я7
Составитель канд. техн. наук А. В. Перова
Методы и модели в расчетах на ЭВМ: методические указания к выпол-
нению лабораторных и практических работ для студентов направления 15.03.05 «Конструкторско-технологическое обеспечение машиностроительных производств» (профили «Конструкторско-технологическое обеспечение машиностроительных производств», «Металлообрабатывающие станки и комплексы», «Технология машиностроения») всех форм обучения / ФГБОУ ВО «Воронежский государственный технический университет»; сост.: А. В. Перова. − Воронеж: Изд-во ВГТУ, 2021. − 24 с.
Содержат краткие теоретические сведения по математическому моделированию в машиностроении, методику и порядок выполнения практических работ, снабжены перечнем рекомендуемой литературы и конкретными примерами моделирования с использованием численных методов.
Предназначены для для студентов направления 15.03.05 «Конструктор- ско-технологическое обеспечение машиностроительных производств» (профили «Конструкторско-технологическое обеспечение машиностроительных производств», «Металлообрабатывающие станки и комплексы», «Технология машиностроения») всех форм обучения.
Методические указания подготовлены в электронном виде и содержатся в файле Методичка_ММврЭВМ.pdf.
Ил. 11. Табл. 5. Библиогр.: 7 назв.
УДК 51:621(075.8) ББК 22.1:34.я7
Рецензент − Е. В. Смоленцев, д-р техн. наук, проф. кафедры технологии машиностроения ВГТУ
Издается по решению редакционно-издательского совета Воронежского государственного технического университета
2
ВВЕДЕНИЕ
Методические указания разработаны для студентов направления 15.03.05 «Конструкторско-технологическое обеспечение машиностроительных производств».
Целью работы является помощь обучающимся в изучении дисциплины, выполнении практических и лабораторных работ. Также приводятся краткие теоретические сведения по математическому моделированию в машиностроении и конкретные примеры моделирования.
В методических указаниях представлены три практических занятия и две лабораторные работы. Дается порядок выполнения практических работ и рекомендации по их выполнению, которые позволят обучающимся систематизировать, углубить и конкретизировать теоретические знания.
3
ПРАКТИЧЕСКАЯ РАБОТА № 1 ОПРЕДЕЛЕНИЕ ЭКСТРЕМУМА ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
Цель работы: теоретическое изучение и получение практических навыков в определении экстремумов функции одной переменной классическим методом.
Теоретические сведения
Функция f(x) действительной переменной x имеет локальный минимум в точке xo, если существует некоторая положительная величина ∆, такая, что еслиx-xo < ∆, то f(x) ≥ f(xо), т.е. если существует окрестность точки xo, такая, что для всех значений x в этой окрестности величина f(x) больше f(xo). Функция f(x) имеет глобальный минимум в точке xmin , если для всех x справедливо неравенство f(x) ≥ f(xmin). С другой стороны функция f(x) имеет локальный максимум в точке xk, если существует некоторая положительная величина ∆, такая, что x-xo < ∆, то f(x) ≤ f(xk) , т.е. если существует окрестность точки xk, для которой при всех значениях x в этой окрестности величина f(x) меньше f(xk). Функция f(x) имеет глобальный максимум в точке xmax, если для всех x справедливо неравенство f(x) ≤ f(xmax).
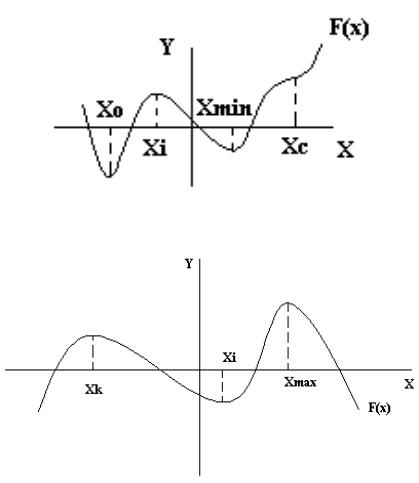
На рис. 1.1. дано графическое представление функции f(x), которая имеет локальный минимум в точке xo и глобальный минимум в точке xmin.
На рис.1.2. дано графическое отображение функции f(x), имеющей локальный и глобальный максимумы в точках xk, xmax.
Классический метод нахождения точек экстремума (точкиxo, xmin, x на рис. 1.1 и точкиxk, xmax, xi на рис.1.2) заключается в поиске уравнений, решением которых являются эти точки. Функцииf(x), представленные на рис. 1.1 и 1.2, и их производные непрерывны, а в точках экстремума первая производнаяf′(x) равна нулю. Т.о. точки экстремума функции f(x) являются решениями уравнения:
f′(x) = 0 |
(1.1) |
При этом необходимо отметить, что решением уравнения (1.1) являются не только точки минимума и максимума функции f(x) (xo, xmin, xi на рис.1.1), но и точка горизонтального перегиба функции xc. Отсюда видно, что уравнение (1.1) является только необходимым условием экстремума, но не является достаточным.
Для определения характера экстремума возникает необходимость рассмотрения более высоких производных функции f(x). В точках локального и глобального минимума (рис. 1.1) xo, xmin первая производная функции f`(x) меняет знак с отрицательного на положительный; в точке xi (рис. 1.1) - с положительного на отрицательный, а в точке xc знак производной не меняется. Т.о. можно сделать вывод о том, что первая производная в минимуме является воз-
4
растающей функцией, а так как степень возрастания f`(x) измеряется второй производной, то для минимума функции f(x) справедливо неравенство f″(xo)>0 , f″(xmin) > 0. Аналогично, для точки максимума xi функции f(x): f″(xi) < 0.
Рис.1.1. Графическое представление функции f(x) имеющей локальные и глобальные минимумы в xo и xmin и
локальный максимум в xi
Рис.1.2. Функция f(x) с локальным в xk и глобальным в xmax максимумами и локальным минимумом в xi
Для определения различия между локальными и глобальными экстремумами необходимо сравнивать значения функции в точках минимума и макси-
мума f(x0) , f(xmin) , f(xi) (рис. 1.1).
Аналогично, данную задачу можно решить, используя разложение функции в ряд Тейлора в окрестностях точки экстремума x0 (xmin, xi) (рис.1.1). Для точки x0 функции f(x) можно записать:
f (x + h) − f (x0 ) = hf |
′ |
h 2 |
f |
′′ |
h3 |
f |
′′′ |
(x0 ) + |
2! |
(x0 ) + |
3! |
(x0 ) +..., |
при этом если в т. x0 достигается минимум, то левая часть уравнения отвечает неравенству f(x0 + h) - f(x0) ≥ 0 для любого достаточно малого значения h: /h/<∆.
Неравенство для случая, если в т. x0 достигается максимум. Выглядит следующим образом: (x0 +h) - f(x0) ≤ 0.
5
Можно сформулировать следующее правило определения характера экстремума функции:
Если функция f(x) и ее производные непрерывны, то точка x0 является точкой экстремума только в том случае, если порядок первой не обращающейся в нуль в точке производной n - четное число. При этом если f(x0) > 0, то в т. x0 достигается максимум, а если f(x0) > 0 - минимум.
Порядок выполнения работы
1.Задание на работу студент выбирает из таблицы 1.2 в соответствии со своим порядковым номером в списке группы.
2.Опираясь на теоретические сведения, приведенные выше, студент вычисляет первую производную исходной функции и определяет значение точек экстремума из уравнения (1.1).
3.Производится вычисление второй производной функции и определяется характер точек экстремума.
4.Определяются точки глобального минимума и максимума функции. Все результаты расчетов по п. 1 - 4 сводятся в табл.1.1.
5.Составляется алгоритм вычисления 1-й и 2-й производной исходной функции и поиска точек экстремума. Блок-схема алгоритма приводится в отчете.
6.Составляется программа на языке программирования для построения кривой исходной функции. Производится проверка результатов, полученных в п. 3-4.
Таблица 1.1
Результаты расчетов
f(x) |
f'(x) |
f"(x) |
|
|
Точки минимума |
|
|
Точки максимума |
|||||
x1min |
x2min |
ximin |
f(x1min) |
f(x2min |
f(ximin |
x1max |
|
x2max |
ximax |
f(ximax |
|||
|
|
|
|
|
|
|
) |
) |
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Содержание отчета
Отчет оформляется в тетради для лабораторных работ грамотно и аккуратно. Он должен содержать следующие разделы:
1.Название и цель работы, краткие теоретические сведения о классическом методе поиска экстремума функции одной переменной.
2.Исходная функция, ее первые и вторые производные, точки экстремума
(табл.1.1).
3.Блок-схема алгоритма.
4.Распечатка программы вычисления производных и построения графика функции и результаты расчета.
5.Сравнение результатов расчета "вручную" и на ЭВМ.
6.Выводы по работе.
6
Таблица 1.2
№ |
|
|
Функция |
№ |
Функция |
||||||
п/п |
|
|
п/п |
||||||||
|
|
|
|
|
|
|
|
|
|
||
1 |
4x3 + 4x 2 + x +1 |
14 |
x 4 −14x3 + 60x 2 +16 |
||||||||
|
|
|
|
|
|
|
|
||||
2 |
x3 − 6x 2 + 4x + 5 |
15 |
2x 4 − 7x3 − 4x 2 |
||||||||
|
|
|
|
|
|
|
|
||||
3 |
x3 − 2x 2 + x +1 |
16 |
5x 2 + lg x |
||||||||
|
|
|
|
|
|
|
|
|
|||
4 |
|
x 4 + x3 − 2x 2 |
17 |
x3 + x lg x |
|||||||
|
|
|
|
|
|
|
|
||||
5 |
2x 4 + 2x3 − 6x 2 +1 |
18 |
x 2 + e x |
||||||||
|
|
|
|
|
|
|
|
||||
6 |
x 4 + 2x3 −5x 2 + 7 |
19 |
x 2 + |
1 |
|
|
|||||
x |
|||||||||||
|
|
|
|
|
|
|
|
e |
|||
7 |
x3 |
−3,5x 2 + 4x |
20 |
1+ x lg x + e x |
|||||||
|
|
|
|
|
|
|
|
||||
8 |
0,3x3 |
+ 3,5x 2 |
+12x + 7,1 |
21 |
− e −x sh( |
x |
) |
||||
|
|||||||||||
|
|
|
|
|
|
|
2 |
|
|||
9 |
0,2x3 |
+1,6x 2 |
−8,4x + 0,5 |
22 |
e −x |
− Sinx |
|||||
10 |
x3 |
− 6x 2 − 28x + 3,1 |
23 |
e −x |
−Cosx |
||||||
11 |
0,3x3 |
+ 6x 2 |
+10x + 5 |
24 |
x(x −1)3 |
||||||
|
|
|
|
|
|
|
|||||
12 |
0,3x3 |
+ 6x 2 |
+10x + 5 |
25 |
3x 2 |
+ Sin 2 x |
|||||
|
|
|
|
|
|
||||||
13 |
|
|
x(x −1)2 |
26 |
2x + Cosx |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
Контрольные вопросы
1.Сформулируйте правило поиска экстремума функции классическим методом.
2.Необходимое и достаточное условие экстремума функции.
3.Для какого типа переменных и функций применим данный метод.
7
ЛАБОРАТОРНАЯ РАБОТА № 1 ОПРЕДЕЛЕНИЕ ЭКСТРЕМУМА ФУНКЦИИ МЕТОДОМ НЬЮТОНА
Цель работы: теоретическое изучение и получение практических навыков численного решения дифференциальных уравнений методом Ньютона.
Теоретические сведения
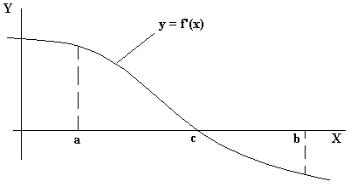
Если существует функция f(x) действительной переменной x непрерывная в каждой точке своей области определения и ее производная f’(x), то для приближенного решения уравнения f’(x) = 0 (т.е. для нахождения точек экстремума) можно построить приблизительный эскиз кривой y = f’(x). При этом можно найти два значения а и в, таких, что f`(a), f`(b) имеют противоположные знаки, то тогда в силу непрерывности функции и ее производной, существует корень
С уравнения f`(x) = 0, отвечающий условию (рис.2.1): |
|
a < c < b |
(2.1) |
В прямоугольной системе координат изобразим график функции y = f`(x) (рис.2.2). Решением уравнения y = f’(x) = 0 является точка К с координатами (xk,0), которые необходимо определить. В точке Р, принадлежащей кривой f’(x), проведем касательную к этой кривой - прямую РТ. Проекцией точки Р на ось абсцисс является точка А с координатами (x0,0). Можно сказать, что точка А является аппроксимацией точки К, а значение координаты x0 - аппроксимацией корня уравнения y = f’(x) = 0. Однако из анализа рис. 2.2. можно сделать
вывод, что точка Т с координатами (x1,0) аппроксимирует корень, лежащий в |
|
точке К лучше, чем точка А. |
|
Для точки Т можно записать следующее равенство: |
|
OT = OA - TA = x0 – TA |
(2.2) |
С другой стороны для касательной РТ к кривой f`(x) справедливо: |
|
PA = tgϕ = f ′′(x0 ) |
(2.3) |
TA |
|
Рис.2.1. Определение корня уравнения кривой y = f’(x)
8
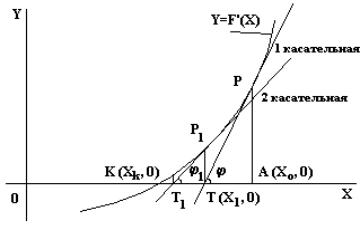
Рис.2.2. Аппроксимация корня дифференциального уравнения
Проведя преобразования выражения (2.3) можно записать:
TA = |
|
PA |
= |
f ′(x0 ) |
(2.4) |
|
f |
′′ |
f |
′′ |
|||
|
(x0 ) |
|
(x0 ) |
|
||
В равенстве (2.2), заменив длину отрезка ОТ на координаты точки Т, получим:
x1 = x0 - TA
Подставив в (2.5) выражение (2.4), имеем:
x1 = x0 |
− |
f ′(x0 ) |
|
f |
′′ |
||
|
|
(x0 ) |
|
(2.5)
(2.6)
Как видно из выражения (2.6) можно определить координату точки Т, являющейся аппроксимацией корня К с определенной точностью.
Для повышения точности аппроксимации в точке Т восстанавливают перпендикуляр к оси абсцисс (рис.2.2), который пересекается с кривой y = f`(x) в точке P1 . В этой точке строят вторую касательную к кривой f`(x), которая пересекает ось абсцисс в точке T1. После этого вся последовательность аппроксимации повторяется:
x2 |
= x1 |
− |
f ′(x1 ) |
(2.7) |
|
f |
′′ |
||||
|
|
|
(x1 ) |
|
|
Количество аппроксимаций зависит от требуемой степени точности результата и в общем виде записывается как:
xi = xi−1 |
− |
f ′(xi−1 ) |
(2.8) |
|
f |
′′ |
|||
|
|
(xi−1 ) |
|
|
9
Точность аппроксимаций определяется требуемой точностью результата по соотношению:
e xi − xi−1
где e - требуемая точность результата.
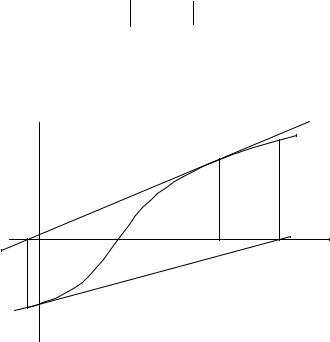
Если начальная аппроксимация корня выбрана неудачно, расхождение результата аппроксимаций (рис. 2.3)
(2.9)
то возможно
Y |
|
y = f'(x) |
|
|
P0 |
||
|
P2 |
|
|
T1 |
T0 |
|
|
0 |
T2 |
X |
|
P1 |
|
|
|
Рис.2.3. Расходящаяся аппроксимация |
|
||
После того как было найдено решение xk уравнения f`(x) = 0 определяется знак второй производной f``(x) в этой точке:
если f``(xk) > 0, то в точке xk достигается минимум функции f(x); если f``(xk) < 0, то в точке xk достигается максимум функции f(x).
Алгоритм нахождения экстремума функции по методу Ньютона представлен на рис.2.4.
Порядок выполнения работы
1.Задание на лабораторную работу студент выбирает из табл.2.1 в соответствии со своим порядковым номером в списке группы.
2.Опираясь на теоретические сведения студент составляет программу на любом языке программирования для решения задачи поиска экстремума функции методом Ньютона. Программа и ее результаты после отладки и проверки должны быть приложены к отчету.
3.Составляется программа построения кривой функции f(x) с масштабом, достаточным для проверки результатов расчетов по п.2 (можно использовать средства построения графиков функций других приложений - Excel или
MathcadPLUS).
10
