Задачи для самостоятельного решения

1. Тонкая лента шириной l=40 см свернута в трубку радиусом R=30см. По ленте течет равномерно распределенный по ее ширине ток I=200A (рис 4.10). Определить магнитную индукцию на оси трубки в двух точках: 1) в средней точке; 2) в точке, совпадающей с концом трубки.

Ответ: В₁=349мкТл, В₂=251мкТл.

2. Однородный ток плотности j течет внутри неограниченной пластины толщины 2d параллельно ее поверхности. Найти индукцию магнитного поля этого тока как функцию расстояния х от средней плоскости пластины. Магнитная проницаемость всюду считать равной единице.

Ответ: ; .

3. Однородный ток I равномерно распределен по бесконечно длинной, очень тонкой металлической ленте шириной 2а. Определить индукцию магнитного поля в точке, расположенной симметрично относительно краев ленты и отстоящей от плоскости на расстоянии а.

Ответ:

4. Однородный ток равномерно распределён по бесконечно длинной, очень тонкой металлической ленте шириной . Определить индукцию магнитного поля в точке, расположенной на перпендикуляре, восстановленном из крайней точки ленты.

_{Ответ: ; ; .}

5. Магнитное поле вращающихся заряженных тел

1. Основные формулы

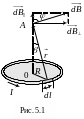
• Индукции магнитного поля на оси витка с током (рис.5.1).

.

• Магнитная индукция в центре кругового проводника с током определяется по формуле

.

Примеры решения задач

1. Тонкий диск радиусом равномерно заряжен до поверхностной плотности заряда . Диск равномерно вращается с угловой скоростью . Определить индукцию магнитного поля: а) в центре диска и б) на расстоянии от центра.

Решение.

а) Рассмотрим кольцо радиуса r и шириной dr (рис. 5.2 a). Элементарная индукция, создаваемая вращающимся кольцом равна

,

где

Интегрируя, найдем

.

б) Элементарная индукции магнитного поля на оси диска(рис. 5.2 б), создаваемая вращением кольца равна

,

где .

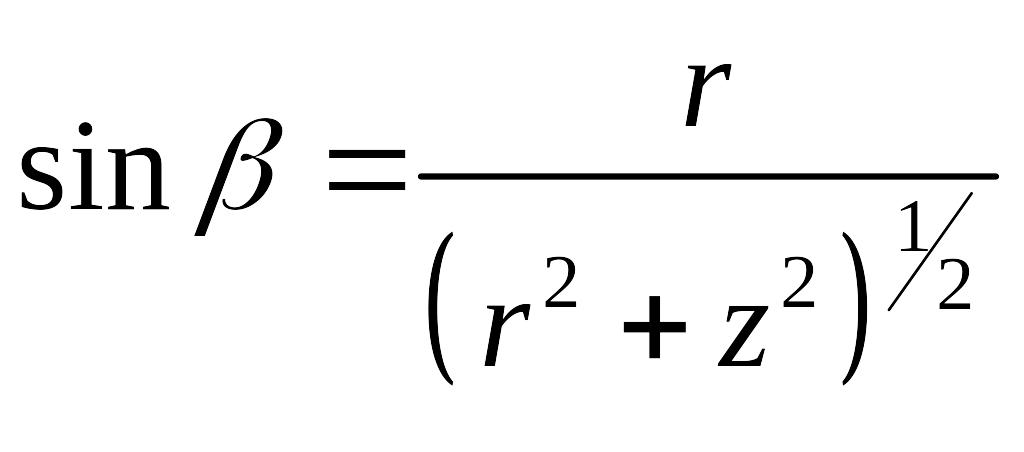Преобразуем данное выражение

; и ,

,

.

В результате интегрирования получим

.

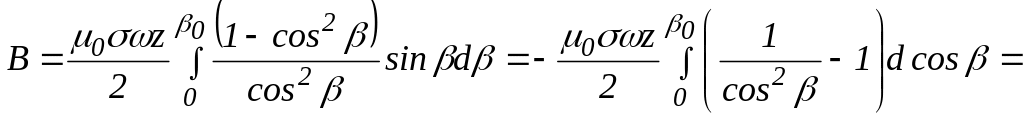
Произведём замену .

Окончательно получаем

.

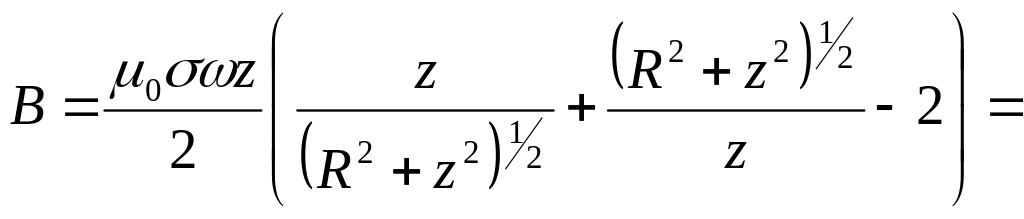
2. Тонкое кольцо с внутренним и внешним радиусами и равномерно заряженное до поверхностной плотности заряда равномерно вращается с частотой относительно оси, перпендикулярной плоскости кольца и проходящей через её центр. Найти индукцию магнитного поля на оси, на расстоянии от центра.

Решение.

Решение данной задачи совпадает с предыдущим, за исключением расчёта интеграла, который берётся в пределах от до (рис. 5.2б).

.

При данная формула совпадает с ответом предыдущей задачи.

3. Тонкостенная металлическая сфера радиусом R имеет равномерно распределённый по её поверхности заряд с поверхностной плотностью . Сфера равномерно вращается с угловой скоростью относительно оси, проходящей через центр сферы. Найти индукцию магнитного поля в центре сферы.

Решение.

В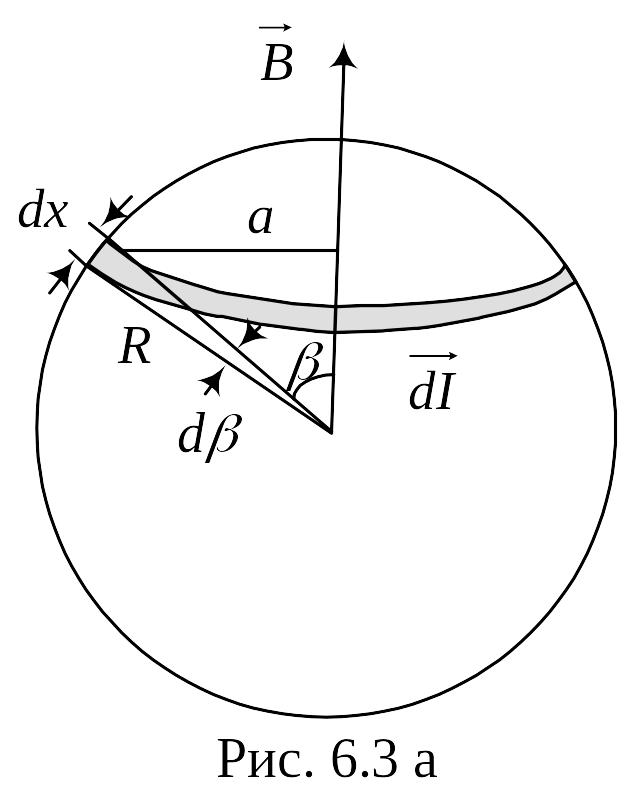 оспользуемся формулой

,

где - радиус вращения элемента поверхности вокруг оси (рис. 5.3а).

Произведем замены

, ,

г

Рис. 5.3 а

де , .

Таким образом,

,

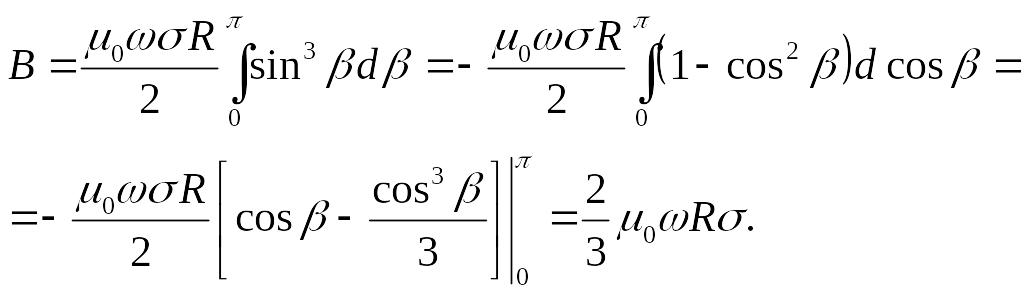
Данную задачу можно решить, используя сферические координаты (рис. 5.3 б),

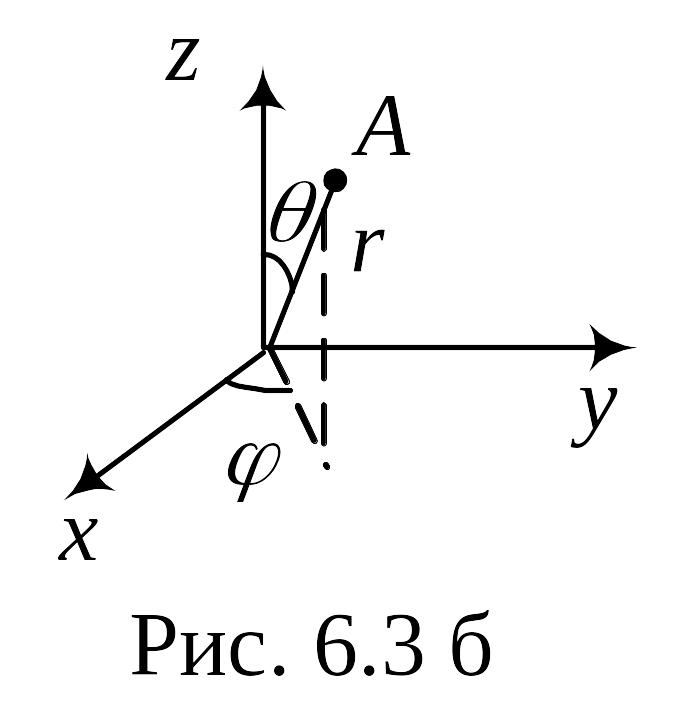^{г де}

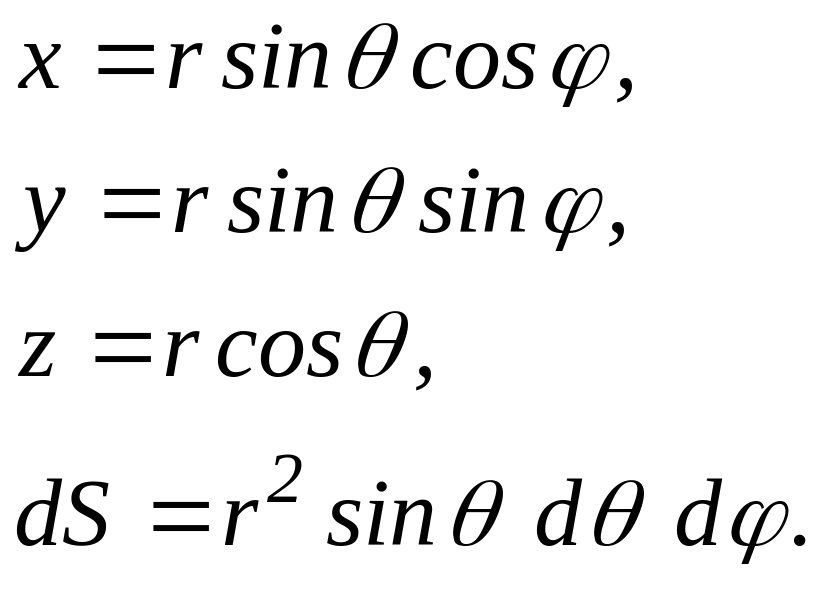
В

Рис. 5.3 б

этом случае рабочая формула принимает вид

,

где .

,

.

4. Сплошной шар радиусом имеет заряд , равномерно распределённый по объёму. Шар вращается относительно оси, проходящей через центр шара, с угловой скоростью . Определить магнитную индукцию в центре шара.

Решение.

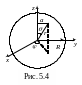
Решим данную задачу, используя сферическую систему координат (рис. 5.4)

Воспользуемся той же формулой, что и в задачах 1, 2 и 3 главы 6.

,

где , 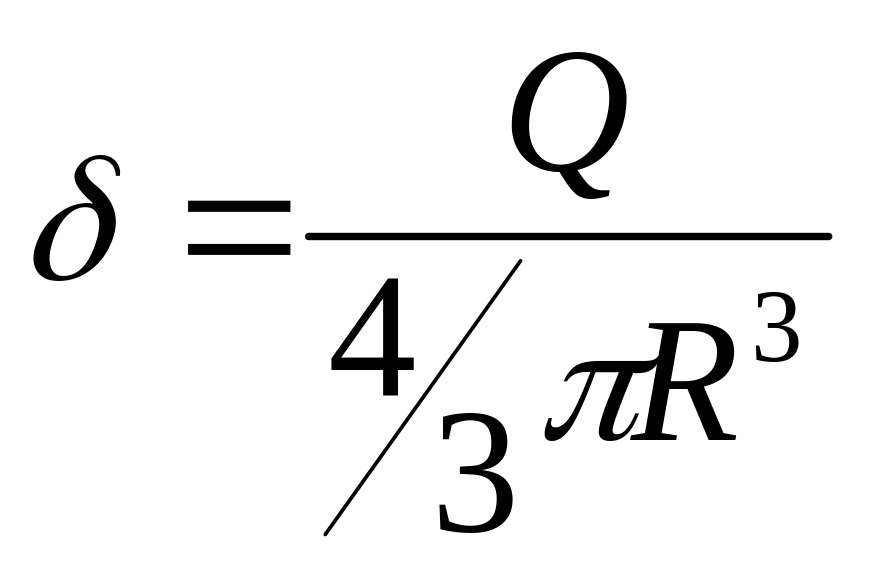- объёмная плотность заряда, а .

После подстановки получим

, .

В результате интегрирования по получим

Учитывая значение , найдем .