
- •Магнитное поле линейных и пространственных проводников с током методические указания
- •Магнитное поле линейных и пространственных проводников с током
- •394026 Воронеж, Московский просп., 14
- •1. Магнитное поле линейных проводников с током Основные законы и формулы
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •2. Магнитное поле соленоида и тороида Основные законы и формулы
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •3. Применение теоремы о циркуляции вектора магнитной индукции к расчёту полей Основные законы и формулы
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •5. Магнитное поле вращающихся заряженных тел
- •Основные формулы
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Библиографический список
- •Содержание
2. Магнитное поле соленоида и тороида Основные законы и формулы
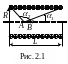
Индукция магнитного поля на оси соленоида конечной длины (рис 2.1)
 ,
,
где – плотность витков; α1 и α2 – углы, под которыми видны края соленоида из точки А, где определяется магнитная индукция.
Индукция магнитного поля на оси длинного соленоида
![]() .
.
Индукция поля тороида
![]() ,
,
где r – радиус выбранного контура.
Если тороид имеет неограниченное число
витков, а его радиус R
стремится к бесконечности, то в пределе
получается выражение аналогичное
магнитному полю бесконечно длинного
соленоида
![]() .
.
Примеры решения задач
1. Катушка длиною 2 см и радиусом 3 см состоит из 1000 витков. Ток, проходящий по катушке равен 200 мА. Найти магнитную индукцию на оси катушки в точке:
а) равностоящей от торцов; б) на одном из торцов; в) отстоящей от торца на расстоянии 2см.
Решение.
 Воспользуемся
формулой для расчета магнитной индукции
соленоида конечной длины ,
Воспользуемся
формулой для расчета магнитной индукции
соленоида конечной длины ,
где
![]() .
.
Согласно рис. 2.2.а ,
 ,
,
![]() ,
,
![]() .
.
Согласно
рис. 2.2.б
![]() ,
,
![]() ,
,

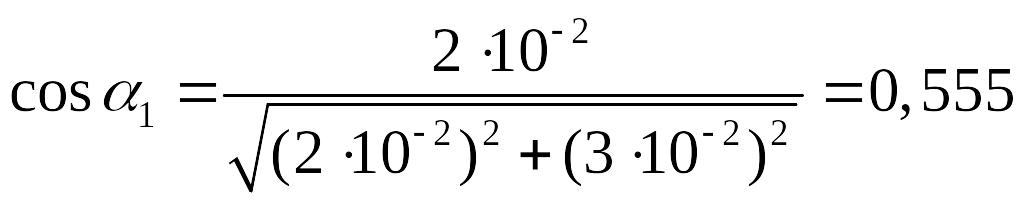 ,
,
![]() .
.
В соответствии с рис. 2.2 в
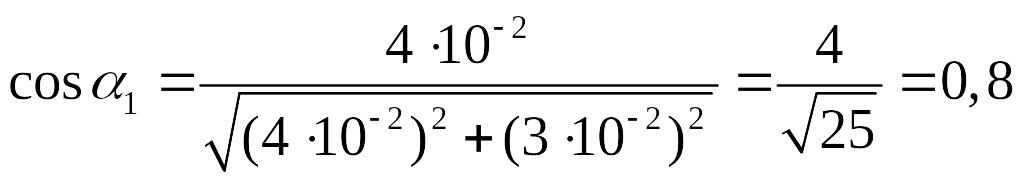
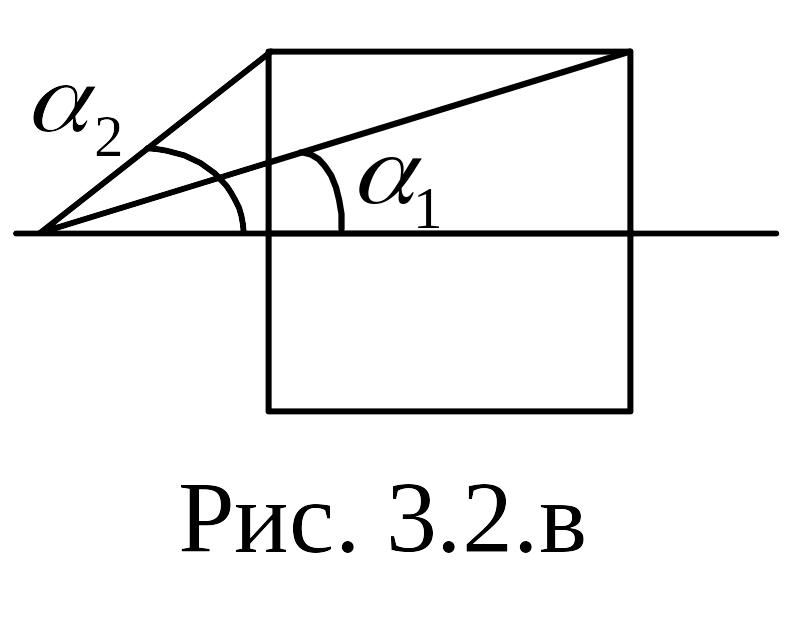 ,
,
Рис. 2.2 в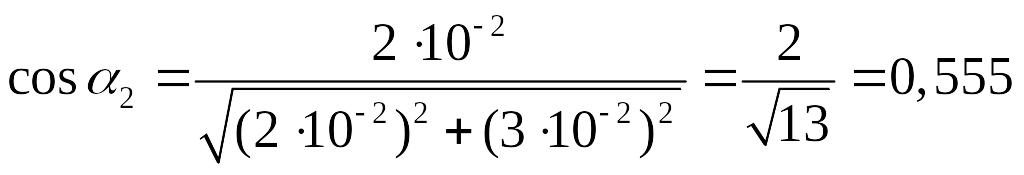
![]() .
.
2. Чему должно быть равно отношение длина катушки к ее диаметру L/D, чтобы магнитную индукцию в центре катушки можно было найти по формуле для поля бесконечно длинного соленоида? Ошибка при таком допущении не должна превышать 1%.
Р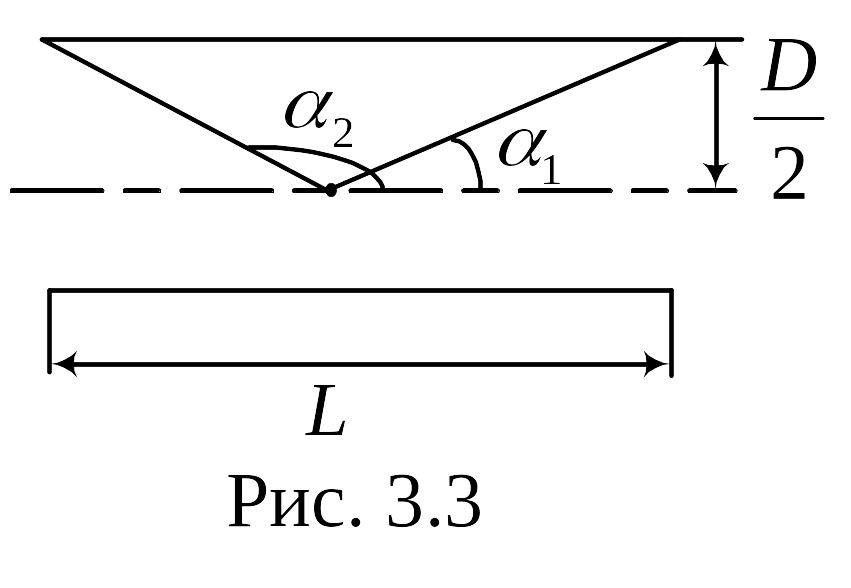 ешение.
ешение.
Относительная
ошибка ищется по следующей формуле ![]() ,
где
,
где
![]() ,
,
Рис. 2.3![]() -
магнитная индукция бесконечно длинного
соленоида.
-
магнитная индукция бесконечно длинного
соленоида.
![]() -
магнитная индукция соленоида конечной
длины, где α
-
магнитная индукция соленоида конечной
длины, где α![]() 1
и α2
1
и α2
![]() –
обозначены на рис. 2.3
–
обозначены на рис. 2.3
![]() ,
,
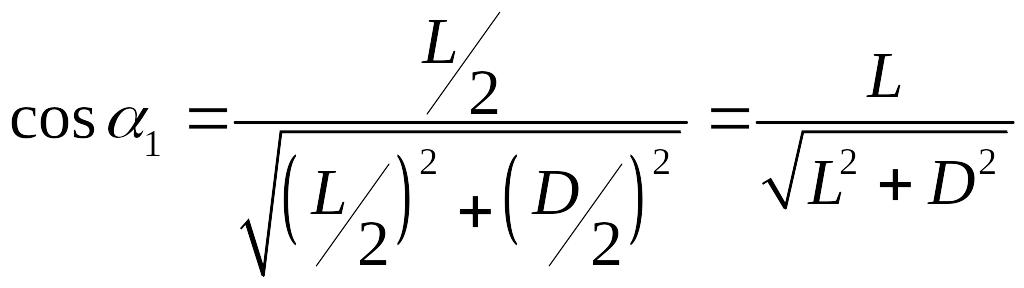 ,
,
![]() .
.
Следовательно
 .
.
После упрощения

![]()
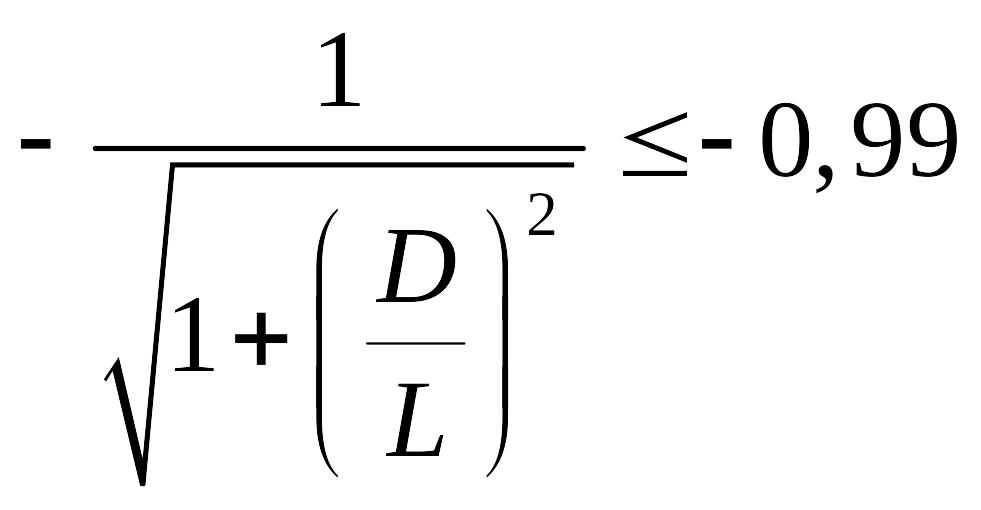 ,
,
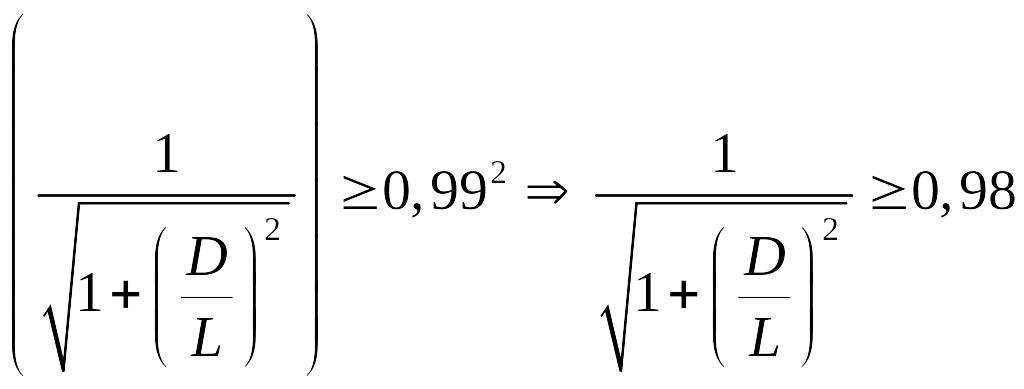 ,
,
![]()
![]() ,
,
![]() .
.
3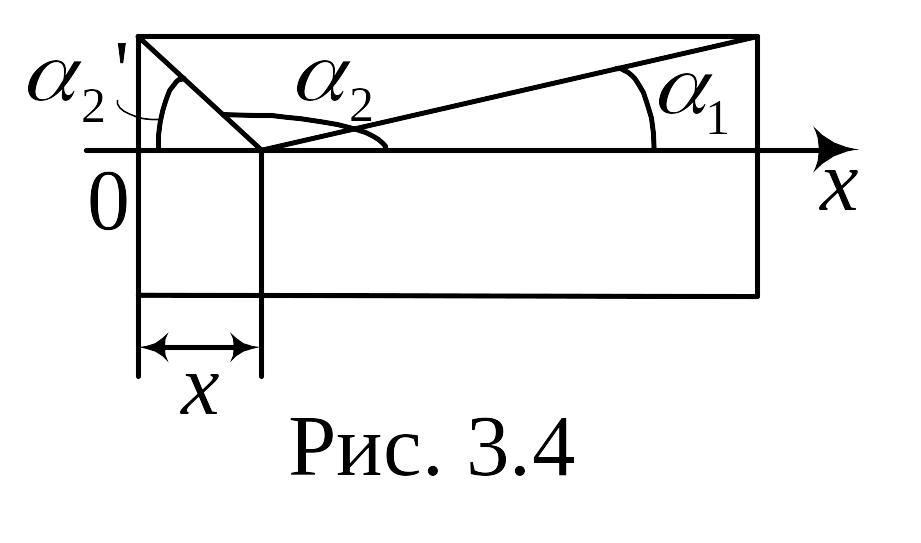 .
Очень длинный прямой соленоид имеет
радиус сечения R
и n
витков на единицу длины. По соленоиду
течет постоянный ток I.
Пусть x
– расстояние, отсчитываемое вдоль оси
соленоида от его торца. Найти:
.
Очень длинный прямой соленоид имеет
радиус сечения R
и n
витков на единицу длины. По соленоиду
течет постоянный ток I.
Пусть x
– расстояние, отсчитываемое вдоль оси
соленоида от его торца. Найти:
а) индукцию магнитного поля на оси как функцию x;
б
Рис. 2.4
Решение.
а) Относительная погрешность определяется по формуле
![]() ,
,
где
;
![]() ,
так как
,
так как ![]() .
.
![]() ,
где
,
где
![]() .
.
Таким образом,
![]() .
.
б) Воспользовавшись соотношением для относительной погрешности, получим:
![]() ;
; ![]() .
.
![]() ;
; ![]() ;
;
![]() ;
;
![]() .
.
![]() ;
;
![]() ,
,
![]() .
.
4.
Однослойная катушка (соленоид) имеет
длину ![]() и радиус сечения R.
Число витков на единицу длины равно n.
Найти индукцию магнитного поля в центре
катушки, если ток через нее равен I.
и радиус сечения R.
Число витков на единицу длины равно n.
Найти индукцию магнитного поля в центре
катушки, если ток через нее равен I.
Решение.
Воспользуемся
формулой для расчета магнитной индукции
на оси витка с током 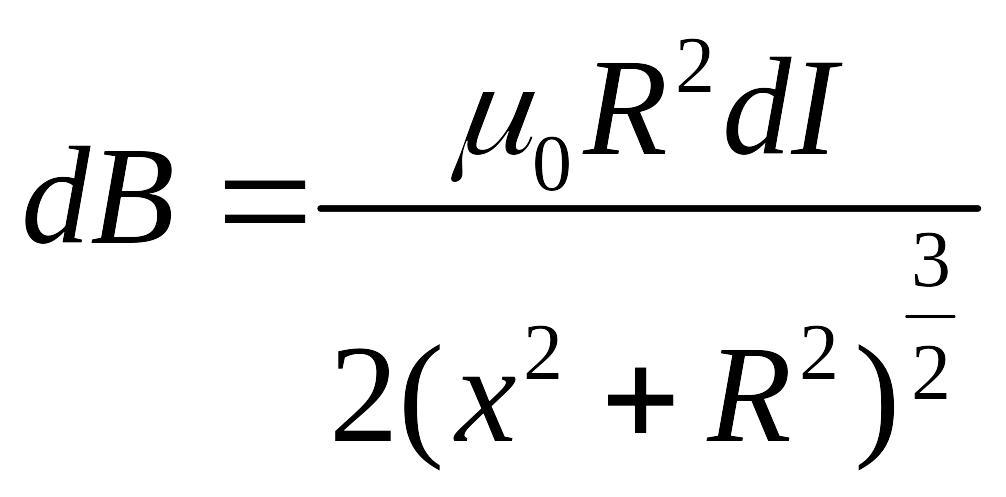 ,
,
где
![]() ,
,
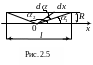
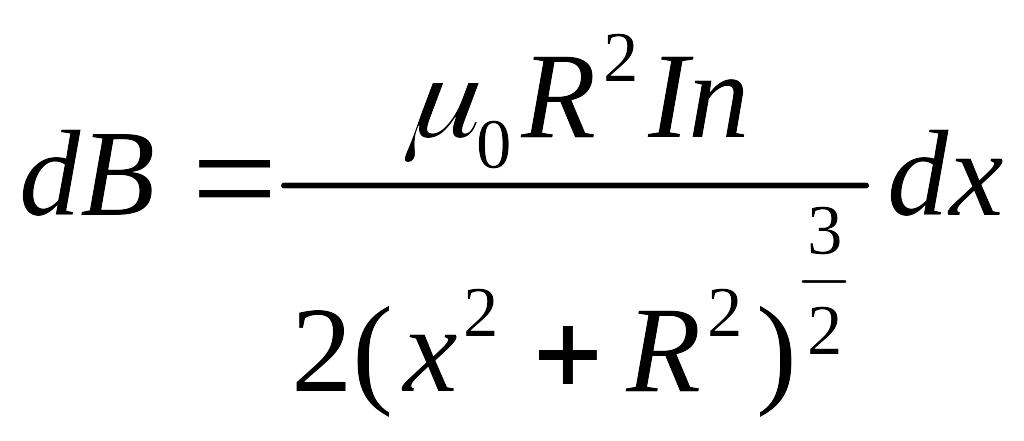 ;
;
![]() .
.
Знак “-” показывает, что с увеличением угла α dx возрастает в отрицательном направлении оси х (см. рис.2.5).
![]() ,
,
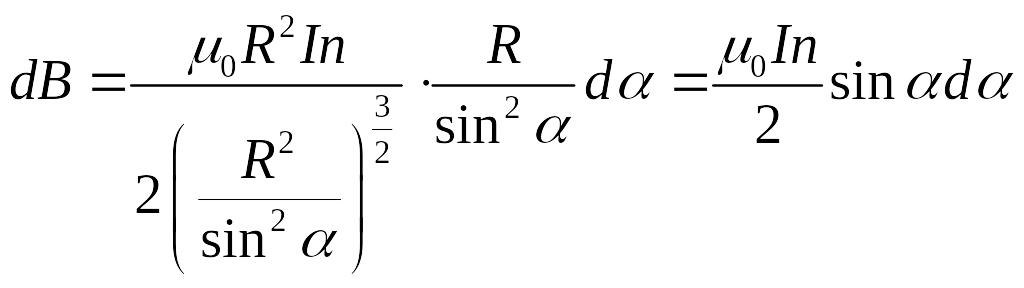 ,
,
![]() ,
,
,
,
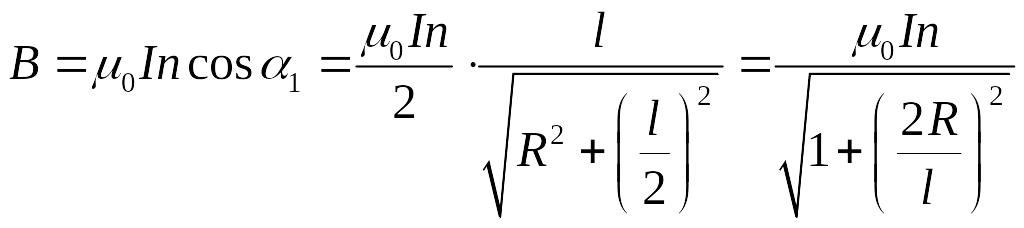 .
.
5. Обмоткой длинного прямого соленоида с радиусом сечения R=2,5 см служит тонкая лента-проводник шириной h=5 см, намотанная в один слой практически вплотную. По ленте течет ток I=5 А. Найти индукцию магнитного поля внутри и вне соленоида как функцию расстояния r от его оси.
Решение.
 Изобразим
схематически
Изобразим
схематически
отрезок ленты, образующий один виток (рис.2.6а). Разложим ток текущий по ленте на две составляющие – параллельную оси соленоида I║ и перпендикулярную I┴ (рис. 2.6 б).
Поле
внутри соленоида создается перпендикулярной
составляющей тока I┴,
а снаружи параллельной составляющей
I║.
Поле внутри соленоида рассчитывается
по известной формуле ![]() ,
где
,
где
![]() - линейная плотность перпендикулярной
составляющей тока.
- линейная плотность перпендикулярной
составляющей тока.
![]() (рис.3.6 б), где
(рис.3.6 б), где ![]() .
.
![]() ;
;
![]() .
.
Для нахождения индукции магнитного поля вне соленоида необходимо использовать теорему о циркуляции вектора магнитной индукции ,
где
,
![]() -линейная
плотность параллельной составляющей
тока.
-линейная
плотность параллельной составляющей
тока.
(рис.2.6
б) =>
![]() .
.
Следовательно
![]() и
и
![]() ,
,
где
![]() (рис. 2.6 а).
(рис. 2.6 а). ![]() ,
где
,
где ![]() .
.
Таким
образом ![]() .
.
6 .
На деревянный
тороид малого поперечного сечения
намотано равномерно N=2,5∙103
витков провода, по которому течет ток
I.
Найти отношение η индукции магнитного
поля внутри тороида к индукции в центре
тороида (рис.2.7).
.
На деревянный
тороид малого поперечного сечения
намотано равномерно N=2,5∙103
витков провода, по которому течет ток
I.
Найти отношение η индукции магнитного
поля внутри тороида к индукции в центре
тороида (рис.2.7).
Р
Рис. 2.7
Индукция магнитного поля внутри тороида рис. 2.7 ищется с использованием теоремы о циркуляции вектора индукции
![]() ,
,
где N – число витков тороида; R – радиус тороида.
Расчет индукции в центре тороида производится по формуле для кругового проводника с током.
![]() ,
, ![]() .
.
7.
Имеется
очень длинный прямой соленоид с током
I.
Площадь поперечного сечения соленоида
S,
число витков на единицу длины n.
Найти поток вектора
![]() через
торец соленоида.
через
торец соленоида.
Решение.
Поток
магнитной индукции в центре соленоида
определяется по формуле
![]() .
.
На
концах соленоида
![]() .
.
 8.
Вычислить магнитный момент тонкого
проводника с током I=0,8
A,
плотно навитого на половину тора (рис.
2.8). Диаметр сечения тора d=5
см, число
витков N=500.
8.
Вычислить магнитный момент тонкого
проводника с током I=0,8
A,
плотно навитого на половину тора (рис.
2.8). Диаметр сечения тора d=5
см, число
витков N=500.
Решение.
Суммарный
магнитный момент формируется параллельными
составляющими
![]() (рис. 2.8 б).
(рис. 2.8 б).
![]() ,
,
где
![]() - число витков на 1 радиан,
- число витков на 1 радиан,
![]() –
число витков,
приходящихся на угловой интервал
–
число витков,
приходящихся на угловой интервал
![]() .
.
В результате интегрирования получим
![]()
