4. Расчёты на жёсткость при изгибе статически определимых систем
4.1. Расчёт балок
4.1. Определить угол поворота сечения А (рис. 4.1), если q = 20кН/м; а = 1м; EJx = const. Проверить жёсткость балки, если [θA] = 0,003 рад; Е = 2·105 МПа; Jx = 2·103 см4.
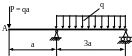
Рис. 4.1
4.2. Определить прогиб сечения А (рис. 4.2), если
q = 20кН/м; а = 2м; Е = 2·105 МПа; EJx = const. Поперечное сечение балки – два двутавра № 12. Проверить жёсткость балки, если [уа] = 0,002а.
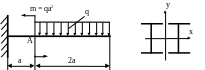
Рис. 4.2
4.3.
Определить угол поворота сечения С
(рис. 4.3), если EJx
= const;
Е = 2·105
МПа; Jx
= 2·103
см4;
м;
кН/м.
Проверить жесткость балки, если
рад.
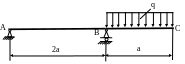
Рис. 4.3
4.4. Определить максимальный прогиб (рис. 4.4), если q=20кН/м; a=1м; Е = 2·105 МПа; EJx = const, сечение балки - швеллер №14. Проверить жесткость балки, если [у] = 0,003а.
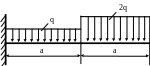
Рис. 4.4
4.5.
Определить угол поворота сечения
(рис. 4.5), если: q
= 20кН/м; a
= 1м; Е = 2·105МПа;
EJx
= const;
Jx
= 2·103
см4.
Проверить жесткость балки, если
рад.
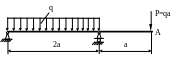
Рис. 4.5
4.6. Определить прогиб сечения А (рис. 4.6), если Р = 10кН; а = 1м; EJx = const; Е=2·105 МПа; сечение балки – двутавр №14. Проверить жесткость балки, если [уA]=0,003a.
Рис. 4.6
4.7. Определить угол поворота сечения С (рис. 4.7), если EJx = const; Е = 2·105 МПа; а = 1м; q = 10кН/м; поперечное сечение балки – швеллер №12. Проверить жёсткость балки, если [θc] =0,002 рад.
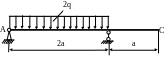
Рис. 4.7
4.8. Определить прогиб в сечении А (рис. 4.8), если ЕJx=const; Е=2·105 МПа; Jx=2·103 cм4; а = 1м; q = 10 кН/м. Проверить жесткость балки, если [уA]=0,003а.
Рис. 4.8
4.9. Определить угол поворота сечения на левой опоре (рис. 4.9), если q = 20 кН/м; ℓ=2м; Е=2·105 МПа; сечение балки - двутавр № 12; ЕJx = const. Проверить жесткость балки, если [θA]=0,003 рад.
Рис. 4.9
4.10. Определить прогиб сечения А (рис. 4.10), если q = 20 кН/м; а = 1м; Р = 10кН; m = 10кНм; ЕJx = const; Е=2·105 МПа. Сечение балки – швеллер №10. Проверить жесткость балки, если [уA]=0,003а.
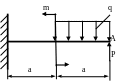
Рис. 4.10
4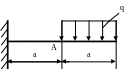
.11.
Определить угол поворота сечения А
(рис. 4.11), если ЕJx
= const;
q
= 20 кН/м; а = 2м; Е=2·105
МПа; Jx
= 2·103
см4.
Проверить жесткость балки, если
[θA]=0,002
рад.
Рис. 4.11
4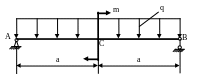
.12.
Определить прогиб сечения С (рис. 4.12),
если ЕJx
= const;
а = 1м; Е=2·105
МПа; q
= 10 кН/м; m
= qа2;
поперечное сечение балки – двутавр
№12. Проверить жесткость балки, если
[уС]=0,002а.
Рис. 4.12
4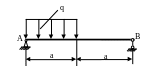
.13.
Определить угол поворота сечения В
(рис. 4.13), если ЕJx
= const;
Е=2·105
МПа; а = 1м; q
= 20 кН/м; поперечное сечение балки –
швеллер №14. Проверить жесткость балки,
если [θB]=0,003
рад.
Рис. 4.13
4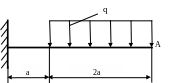
.14.
Определить прогиб в сечении А (рис.
4.14), если ЕJx
= const;
Е=2·105
МПа; а = 0,5м; q
= 10 кН/м; Jx
= 1000см4.
Проверить жесткость балки, если
[уА]=0,002а.
Рис. 4.14
4
.15.
Определить угол поворота сечения А
(рис. 4.15), если EJx
= const;
E
= 2·105
МПа; Jx=2·103
cм4;
М = qa2;
а = 1 м; q
= 10 кН/м. Проверить жёсткость балки, если
[θA]=0,002
рад.
Рис. 4.15
4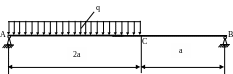
.16.
Определить прогиб сечения С (рис. 4.16),
если EJx
= const;
E
= 2·105МПа;
q
= 10 кН/м; а=1 м; Jx
= 2·103
cм4.
Проверить жёсткость балки, если
[уC]=0,003а.
Рис. 4.16
4.17. Определить угол поворота сечения А (рис. 4.17), если EJx = const; а = 1м; q = 10 кН/м; поперечное сечение балки – двутавр № 16. Проверить жёсткость балки, если [θA]=0,003 рад.
q
A
B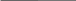
а
а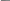
Рис. 4.17
4
.18.
Подобрать номер стального швеллера,
для заданной балки (рис. 4.18), из условий
прочности и жёсткости, если допускаемое
напряжение
=160МПа,
а допускаемый прогиб [y]
= ℓ/400. Сравнить веса балок, получаемые
из условий прочности и жёсткости. Принять
E
= 2·105
МПа; EJx
= const.
Рис. 4.18
4.19. Определить угол поворота сечения А (рис. 4.19), если q = 20 кН/м, EJx = const, а = 1м, E = 2·105 МПа, поперечное сечение балки – двутавр №10. Проверить жёсткость балки, если [θA]=0,003 рад.
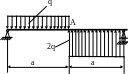
Рис. 4.19
4.20. Балка длиной ℓ = 1 (рис. 4.20), изогнута по дуге окружности моментом m. Сечение балки – прямоугольник со сторонами b = 6 см, h = 4 см. Прогиб максимальный ymax = 6 мм. Определить модуль упругости материала балки Е и радиус кривизны её оси ρ, если допускаемое нормальное напряжение =10МПа.
Рис. 4.20
4
.21.
Определить угол поворота сечения А
(рис. 4.21), если q
= 20 кН/м; а = 1м; E
= 2·105МПа,
а сечение балки – двутавр № 12. Проверить
жёсткость балки, если [yA]=0,002а.
Рис. 4.21
4.22. Какую силу P нужно приложить к балке (рис. 4.22), чтобы обеспечивалось условие: ymax ≤ 0,002a, если EJx = const; а = 2м; q = 5 кН/м. Поперечное сечение балки – двутавр № 10.
Рис. 4.22
4.23. Для заданной балки (рис. 4.23) подобрать номер стального швеллера из условия жёсткости, если [y] = 0,002ℓ; q = 10кН/м; ℓ = 2м; E = 2·105МПа; P = 5кН; EJx = const.
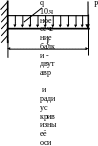
Рис. 4.23
4.24. При нагружении сосновой доски (рис. 4.24), грузом P = 4кН, был зафиксирован максимальный прогиб под грузом ymax = 2мм. Определить модуль упругости сосны, если ℓ = 1м; b = 200мм; h = 10мм.
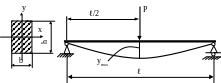
Рис. 4.24
4.25.
Стальная двутавровая балка
,
защемленная одним концом, пролетом
нагружена равномерно распределенной
нагрузкой интенсивностью
.
Какую сосредоточенную силу
можно приложить дополнительно на
свободном конце балки, чтобы наибольшие
нормальные напряжения не превышали
?
Наибольший прогиб при этом не должен
превышать
пролета
балки. Принять E
= 2·105МПа.
4.26.
Определить прогиб балки в сечении
(рис. 4.25), если ℓ = 1м; q
= 20кН/м; а = 40мм; E
= 2·105МПа;
EJx
= const.
Проверить жесткость балки, если
.
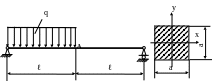
Рис. 4.25
4.27.
Балка с пролетом ℓ = 1 м, свободно лежащая
на двух шарнирных опорах, изогнута по
дуге окружности. Сечение балки
прямоугольное со сторонами
6
см;
4
см. Прогиб посередине пролета прогиб у
= 6,25 мм. Определить модуль упругости и
радиус кривизны оси балки, если наибольшее
нормальное напряжение
=
=10
МПа.
4.28. Определить прогиб сечения А (рис. 4.26), если
10
кНм;
1
м;
2·105
МПа; Jx=2·105мм4;
EJx
= const.
Проверить жесткость балки, если
[уA]=0,003а.
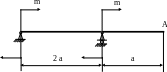
Рис. 4.26
4.29.
Определить прогиб в сечении С (рис.
4.27), если: EJx=const;
E=2∙
MПа;
a=1м;
P=qa;
q=20кН/м;
поперечное сечение балки - швеллер №10.
Проверить жесткость балки, если
[ус]=0,003a.
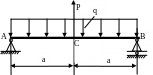
Рис. 4.27
4.30.
Определить прогиб в сечении А (рис.
4.28), если ℓ=1м; q=20кН/м;
Jx=2∙
см4;
Е=2∙
MПа;
EJx
= const.
Проверить жесткость балки, если
[уA]=0,003ℓ.
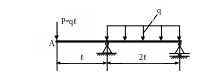
Рис. 4.28
4
.31.
Определить прогиб сечения А (рис. 4.29), и
проверить жесткость балки, если m
= 10 кНм;
1
м; [уA]
= 3мм; EJx
= const;
Е=2∙
MПа.
Рис. 4.29
4.32. Определить прогиб сечения А (рис. 4.30) и проверить жесткость балки, если Р = 50кН; q=20кН/м; 1 м; Е=2∙ MПа; [уA]=0,003а; EJx = const. Сечение балки – швеллер №18.
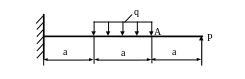
Рис. 4.30
4.33. Консольная балка нагружена распределённой по линейному закону нагрузкой (рис. 4.31). Определить угол поворота сечения А, если q = 20 кН/м; а = 2м; ЕJх=2·105МПа; [θA] = 0,003 рад.
Рис. 4.31
4.34. Определить прогиб сечения А (рис. 4.32) и подобрать сечение балки в форме квадрата, если [уА]=0,001а; Е=2∙105 MПа; а=3м; q= 40 кН/м; ЕJx = const.
Рис. 4.32
4.35. Определить перемещение δ точки А круглого бруса (рис. 4.33) диаметром d=100 мм, если Р=10кН; ℓ=1м; Е=2·105 МПа; ЕJx = const; EF=const. Проверить жесткость бруса, если [δA]=0,001ℓ.
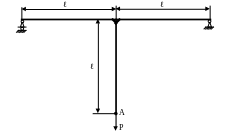
Рис. 4.33
4.36. Определить прогиб в точке А (рис. 4.34) для балки постоянной жесткости ЕJx. Подобрать значение интенсивности равномерно распределенной нагрузки q, е сли Е = 2·105 МПа; а = 1м; [уA] = 0,001а; поперечное сечение балки – швеллер № 10.
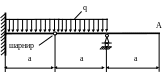
Рис. 4.34.
4.37. Определить положение точки перегиба изогнутой оси балки (рис. 4.35) и угол поворота θA на левой опоре, если m = 10кНм; ℓ = 2м; ЕJx = const; Е = 2·105 МПа. Подобрать сечение балки в форме швеллера, если [θА] = 0,003рад.
Рис. 4.35
4.38. Определить угол поворота в одной из опор (А или В) (рис. 4.36) и проверить жесткость балки, если [θА] = [θВ] = 0,003рад; ЕJx = const; q = 20 kН/м; ℓ = 2м; Е = 2·105 МПа; сечение балки – двутавр № 12.
Рис. 4.36
4.39.
Для стальной балки, поперечное сечение
которой состоит из двух двутавров №10
(рис. 4.37), определить угол поворота
сечения А (
;
ЕJx=const;
Е = 2·105
МПа;
)
и проверить жесткость балки, если
.
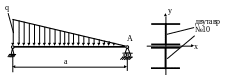
Рис. 4.37
4.40. Методом Мора найти прогиб сечения А (рис. 4.38) и подобрать сечение балки в форме швеллера, если Е = 2·105 МПа; [уА]=0,001а; Р = 20кН; а = 1м; ЕJx=const.
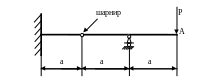
Рис. 4.38
4.41. Найти прогиб сечения А (рис. 4.39) и подобрать сечение балки в форме двутавра, если [yА] = 0,001а; Е = 2·105 МПа; Р = 10 кН; m = 20 кНм; ЕJx =const; а = 1м.
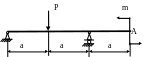
Рис. 4.39
4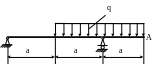
.42.
Найти угол поворота сечения А (рис. 4.40)
и подобрать сечение балки в форме
швеллера, если [θА]
= 0,001рад; Е = 2·105
МПа; q
= 20кН/м; а = 1м; ЕJx
=const.
Рис. 4.40
4
.43.
Найти прогиб сечения А (рис. 4.41) и подобрать
сечение балки в форме квадрата, если Е
= 2·105 МПа;
[yА]
= 0,002а; Р = 20 кН; m
= 10 кНм; а = 1м; ЕJx
=const.
Рис. 4.41
4.44. Определить угол поворота сечения А (рис. 4.42) и подобрать сечение балки в форме швеллера, если Е = 2·105 МПа; [θА] = 0,003рад; q = 20кН/м; m = 10 кНм; а = 1м; ЕJx =const.
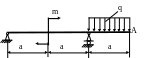
Рис. 4.42
4.45. Определить прогиб сечения А (рис. 4.43) и подобрать сечение балки в форме круга, если Е = 2·105 МПа; [yА] = 0,003а; а = 1м; q = 20кН/м; m = 20 кНм ; ЕJx =const.
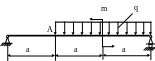
Рис. 4.43
4.46. Определить угол поворота сечения В (рис. 4.44) на правой опоре и подобрать сечение балки в форме двутавра, если Е = 2·105 МПа; [θВ]= 0,002 рад; q = 20кН/м; m =10кНм; а=1 м; ЕJx = const.
Рис. 4.44
4.47. Для стальной балки, поперечное сечение которой – двутавр №10 (рис. 4.45), определить угол поворота сечения В и прогиб сечения С. Принять q = 20кН/м; а = 2м; Е = 2·105 МПа; ЕJx = const. Проверить жесткость балки, если [θВ]= 0,003 рад; [yC] = 0,003a.
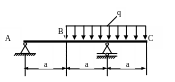
Рис. 4.45
4.48. Найти прогиб сечения А (рис. 4.46) и подобрать сечение балки в форме квадрата, если [yА] = 0,003а; Е = 2·105 МПа; q = 20кН/м; а = 1м; ЕJx = const.
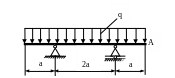
Рис. 4.46
4.49.
Найти угол поворота сечения А (рис. 4.47)
и подобрать сечение балки в форме
швеллера, если [θ
]
= 0,001 рад; Е = 2
5
МПа; Р = 10кН; q
= 10кН/м;
а = 1м; EJx= const.
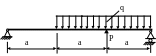
Рис. 4.47
4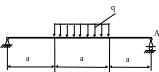
.50.
Найти угол поворота сечения А (рис. 4.48)
и проверить жесткость балки, если EJx=
const;
[θ
]
=0,002 рад; q
= 20кН/м; а = 1м. Сечение балки – двутавр
№10, материал – сталь (Е= 2
5МПа).
Рис. 4.48
4.51. Найти прогиб сечения А (рис. 4.49) и подобрать сечение балки в форме двутавра, если Е=2·105 МПа; [уА]=0,001а; Р=20кН; m=10кНм; а=1м; EJx = const.
Рис. 4.49
4.52. Определить прогиб сечения А (рис. 4.50) посередине пролёта и проверить жёсткость балки, если [уА]=0,002а; а = 1м; q = 20кН/м; Е=2·105 МПа; сечение балки – двутавр № 10.
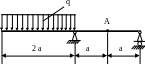
Рис. 4.50
4.53. Определить значение силы (рис. 4.51), если вызванный ею прогиб сечения равен 2мм. Материал балки - сталь, МПа. Принять EJx = const; м; сечение балки – квадрат со стороной 30мм.
Рис. 4.51
4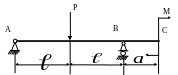
.54.
При какой длине «а»
консоли прогиб сечения С будет равен
нулю (рис. 4.52), если ЕJx
= const;
Е=2·105 МПа;
ℓ = 1м; Р = 10 кН; М = 10 кНм; сечение балки –
двутавр № 10?
Рис. 4.52
4.2. Расчёт плоских рам
4.55.
Проверить жёсткость рамы (рис. 4.53) в
точке А, если допускаемое вертикальное
перемещение [уА]
= 1 см; ЕJx
= const;
Е=2·105 МПа;
сечение – швеллер № 18.
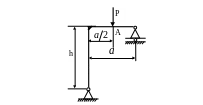
Рис. 4.53
4.56.
Определить
вертикальное смещение уА
сечения А и подобрать сечение рамы
(рис. 4.54)
в форме круга, если Е=2·105
МПа; [уА]
= 2 см;
ЕJх
= const.
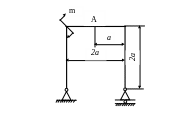
Рис. 4.54
4.57. Определить угол поворота θА сечения на левой опоре рамы (рис. 4.55), если материал – сталь; Е=2·105 МПа; ЕJх = const; сечение – двутавр № 10; а = 100 см; Р = 6кН. Проверить жесткость рамы, если [θА] = 0,003 рад.
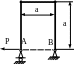
Рис. 4.55
4.58. Подобрать размер поперечного сечения рамы (рис. 4.56) в форме двутавра и определить горизонтальное смещение хА сечения А, если Е=2·105 МПа; ЕJх = const; а = 2м; Р=20кН; m=10кНм; [σ] = 100 МПа. Проверить жесткость рамы, если [хА] = 3мм.
а
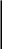
а
Р
а
m
A
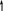
Рис. 4.56
4.59. Определить вертикальное перемещение уА сечения А (рис. 4.57), если а = h = 2м; Р = 20кН; Е=2·105 МПа; ЕJх = const; сечение – прямоугольник с размерами 5×10см. Проверить жесткость рамы, если [уА] = 3мм.
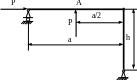
Рис. 4.57
4.60. Найти вертикальное смещение уА сечения А (рис. 4.58), если а = 2м; q = 20кН/м; Р = 20кН; Е=2·105 МПа; ЕJх = const; сечение – два швеллера № 12. Проверить жесткость при [уА] = 5мм.
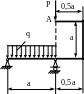
Рис. 4.58
4.61. Подобрать поперечное сечение рамы (рис. 4.59) в форме двух двутавров (Е=2·105 МПа), если а = 2м; q = 20кН/м; [σ] = 160 МПа; ЕJх = const. Допускаемое значение вертикального смещения [уА] точки А равно 5мм.
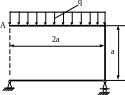
Рис. 4.59
4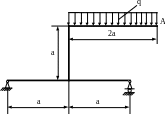
.62.
Подобрать поперечное сечение рамы (рис.
4.60) в форме двух двутавров и определить
угол поворота сечения А. Материал –
сталь Ст. 5 (Е=2·105
МПа).
Проверить жёсткость рамы, если [θА]
= 0,003 рад; ЕJх
= const;
а = 2м; q
= 20кН/м; [σ] = 100 МПа.
Рис. 4.60
4.63. Подобрать размер поперечного сечения рамы (рис. 4.61) в форме двутавра из условия, что сближение точек А и В не должно превышать 5мм. Принять а = 2м; q = 20кН/м; Р = 10кН; Е = 2·105 МПа; ЕJх = const.
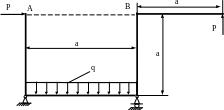
Рис. 4.61
4.64. Сечение рамы (рис. 4.62) – два уголка № 8 (80×80×8мм). Определить угол поворота сечения А и проверить жёсткость рамы, если [θА] = 0,002 рад. Принять а = 2м; q = 20кН/м; Е=2·105 МПа; ЕJх = const.
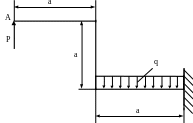
Рис. 4.62
4.65. Подобрать размер поперечного сечения рамы (рис. 4.63) в форме квадрата из условия, что горизонтальное смещение опоры А не должно превышать 5мм. Допускаемое напряжение =100МПа. Модуль упругости Е=2·105 МПа; а=2м; ЕJх=const; q=20 кН/м.
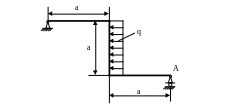
Рис. 4.63
4.66. Подобрать размер поперечного сечения рамы (рис. 4.64) в форме круга и определить угол поворота на одной из опор. Проверить жёсткость рамы, если [θA]=[θB]=0,003 рад. Принять а=2м; =100МПа; Е=2·105 МПа; ЕJх=const.
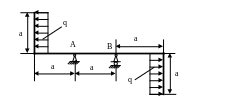
Рис. 4.64
4.67. Подобрать размер поперечного сечения рамы (рис. 4.65) в форме двутавра, чтобы сближение точек А и В не превышало 5мм, а угол поворота сечения С не превышал 0,01 рад. Принять а=2м; q=20 кН/м; Р=10кН; Е=2·105 МПа; ЕJх=const.
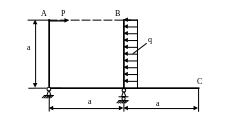
Рис. 4.65
4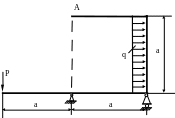
.68.
Подобрать размер поперечного сечения
рамы (рис. 4.66) в форме квадрата и определить
угол поворота сечения А. Проверить
жесткость рамы, если
рад.
Принять
м;
кН/м;
кН/м;
МПа;
МПа;
ЕJх=const.
Рис. 4.66
4.69. Подобрать размер поперечного сечения рамы (рис. 4.67) в форме двух швеллеров из условия, что вертикальное смещение точки А не должно превышать 2мм. Принять м; кН/м; МПа; ЕJх=const.
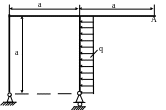
Рис. 4.67
4.70. Подобрать поперечное сечение рамы (рис. 4.68) в форме квадрата из условия, что угол поворота сечения А не должен превышать 0,01 рад. Принять а = 2м; кН/м; Р = 20кН; МПа; ЕJх=const.
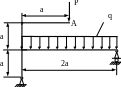
Рис. 4.68
4.71. Подобрать поперечное сечение рамы (рис. 4.69) в форме двух двутавров из условий прочности и жесткости, если а = 2м; кН/м; Р = 40кН; МПа; ЕJх=const; [σ]=200МПа; допускаемое вертикальное перемещение [уА] точки А равно 3мм.
Рис. 4.69
4.72. Определить вертикальное перемещение уА сечения А и проверить жесткость рамы (рис. 4.70), если [уА] = 5мм; а = 2м; кН/м; Р = 40кН. Материал – сталь, МПа. Сечение – квадрат 15×15см; ЕJх=const.
Рис. 4.70
4.73. Подобрать размер поперечного сечения рамы (рис. 4.71) в форме двух швеллеров, исходя из условия, чтобы точки А и В сблизились не более чем на 10мм. Принять ЕJх = const; а = 2м; кН/м; Р = 10кН. Материал – сталь, МПа.
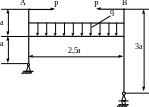
Рис. 4.71
4.74. Подобрать размер поперечного сечения рамы (рис. 4.72) в форме двутавра и определить горизонтальное смещение хА правой опоры A. Материал – сталь, ЕJх=const; а = 2м; кН/м; [σ]=100МПа.
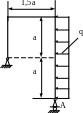
Рис. 4.72
4.75. Подобрать размер поперечного сечения рамы (рис. 4.73) в форме квадрата и определить горизонтальное перемещение xA сечения A. Проверить жесткость рамы, если [xА] = 2мм. Принять ЕJх = const; a = 2м; q = 20кH/м; P =20 кН; [σ] = 160 мПа; Е = 2·105 МПа.
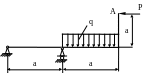
Рис. 4.73
4.76. Найти вертикальное смещение уА точки А и проверить жесткость рамы (рис. 4.74), если [уА] = 3 мм. Принять EJx = const; a = 2м; q = 20 кН/м; m = 10 кНм; Е = 2·105 МПа. Сечение – 2 швеллера № 12.
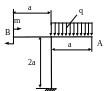
Рис. 4.74
4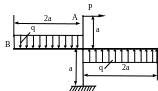
.77.
Определить величину силы Р, чтобы точка
В (рис. 4.75) не сместилась по вертикали.
Принять а=2м; q
= 20кН/м; Е= 2
5
МПа; EJ
=
const.
Сечение - двутавр № 18.
Рис. 4.75
4.78. Определить горизонтальное перемещение х сечения А посередине вертикального участка рамы (рис. 4.76). Проверить жесткость рамы, если [х ]=2 мм. Принять а = 2м; q = 20кН/м; Р=10 кН. Материал - сталь, Е= 2 5 МПа. Сечение – швеллер № 18; EJ = const.
Рис. 4.76
4.79. Определить угол поворота θ сечения А и проверить жесткость рамы (рис. 4.77), если [θ ] = 0,001 рад. Принять а = 2м; h= 3 м; q = 20кН/м; Е= 2 5 МПа; EJ = const. Сечение – двутавр № 10.
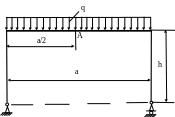
Рис. 4.77
4.80.
Подобрать размер поперечного сечения
рамы (рис. 4.78) в форме двутавра и определить
горизонтальное смещение хA
точки А. Проверить жесткость рамы, если
[х
]
= 3мм. Принять Е= 2
5
МПа;
;
EJ
=
const;
;
.
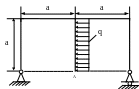
Рис. 4.78
4.81.
Найти вертикальное смещение yA
точки А рамы (рис. 4.79). Проверить жесткость
рамы, если
.
Принять a
= 2м; h
= 1,5м;
;
;
Е= 2
5
МПа; EJ
=
const.
Сечение – квадрат
.
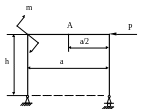
Рис. 4.79
4.82.
Найти сближение точек А и В рамы (рис.
4.80). Сечение стержней на всех участках
одинаковое – квадрат со стороной b=5см.
Проверить жесткость рамы, если [хА]
= [хB]
= 2мм. Принять
;
;
;
Е= 2
5
МПа. Жесткость EJ
=
const.
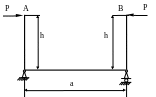
Рис. 4.80
4.83. Определить угол поворота θА сечения А и проверить жесткость рамы (рис. 4.81), если [θА] = 0,003рад. Принять а = 1м; EJ = const. Сечение – швеллер №12.
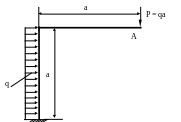
Рис. 4.81
4.84. Определить размер поперечного сечения рамы (рис. 4.82) в форме квадрата из условия, что горизонтальные смещения сечений А и В не должны превышать 10 мм (модуль упругости Е = 2·105 МПа). Принять а =2м; Р = 10 кН; ЕJх =const.
Рис. 4.82
4.85. К балке (рис. 4.83) на двух опорах пролетом 2а прикреплена жестко на правом конце стойка высотой а = 2м. К верхнему концу стойки приложена горизонтальная сила Р = 9 кН. Сечение балки и стойки – двутавр №16. Определить угол поворота θА посередине пролета балки. Проверить жесткость балки, если [θА] = 0,001рад; Е = 2·105 МПа.
Рис. 4.83
4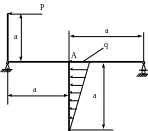
.86.
Подобрать размер поперечного сечения
рамы (рис. 4.84) в форме квадрата и определить
угол поворота θА
в точке А. Mатериал
– сталь; Е = 2·105
МПа. Проверить
жесткость рамы, если [θА]
= 0,003рад. Принять ЕJх
=const;
а = 2м; q
= 20кН/м; Р = 10 кН;
= 100 МПа.
Рис. 4.84
4.87. Проверить жесткость рамы (рис. 4.85), если [yA] = 2мм. Принять Е = 2·105 МПа; ЕJх =const; q = 40кН/м; m = 20кНм; а = 1м; [σ] = 200 МПа. Поперечное сечение – двутавр № 18.
Рис. 4.85
4.88. Определить угол поворота θА сечения А и проверить жесткость рамы (рис. 4.86), если [θА] = 0,002 рад. Принять ЕJх =const; а = 3м; h = 1м; q = 10кН/м; Р = 20кН; Сечение – швеллер № 10; Е = 2·105 МПа.
Рис. 4.86
4.89. Найти вертикальное смещение уА сечения А и проверить жесткость рамы (рис. 4.87), если [уА] = 3мм, Е = 2·105 МПа, ЕJх =const. Принять а = 2м; q = 20кН/м; Р = 10кН. Сечение – швеллер № 10; материал – сталь Ст.3.
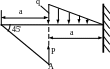
Рис. 4.87
4.90. Подобрать размер поперечного сечения рамы (рис. 4.88) в форме круга, чтобы сечение А повернулось не более чем на 0,01 рад. Принять, а = 2м; q = 20кН/м; m = 20кНм; Е = 2·105 МПа, ЕJх =const.
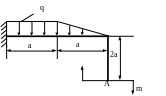
Рис. 4.88
4.91. Определить угол поворота θA сечения А рамы (рис. 4.89), если жёсткость участка AB равна EJx, а участка BC – 2EJx. Проверить жёсткость рамы, если [θА]=0,003рад. Принять Е=2·105 МПа; Р=10кН; М=10кНм; а=1м; поперечное сечение рамы – двутавр №10.
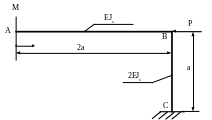
Рис. 4.89