2. Расчеты на прочность и жесткость при кручении круглых валов

2.1. Статически определимые валы

2.1. Определить диаметры ступеней вала (рис. 2.1), если МПа; а = 3м; b = 2м; М₁ = 900 Нм; М₂ = 400 Нм; М₃ = 500 Нм. Определить угол поворота сечения А по отношению к сечению В. Принять МПа.

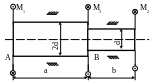
Рис. 2.1

2.2. Определить диаметры вала (рис. 2.2) и полный угол закручивания, если m = 200 Нм; а = 0,2м; МПа; МПа.

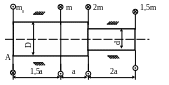
Рис. 2.2

2.3. Определить диаметры d и D вала (рис. 2.3), если m = 0,8 кНм; МПа; ; МПа; а = 1м.

Рис. 2.3

2.4. Определить диаметры вала (рис. 2.4) и полный угол закручивания, если МПа; m = 500 Нм; а = 1 м; МПа; [φ] = 2˚.

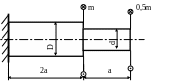
Рис. 2.4

2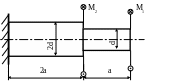 .5. Определить диаметры ступеней вала (рис. 2.5) и полный угол закручивания, если МПа; а = 1м; M₁ = 100Нм; М₂ = 500Нм; МПа.

Рис. 2.5

2.6. Определить диаметры вала (рис. 2.6) из условий прочности и жесткости, если m = 1кНм; МПа; [φ] = 2˚; МПа; а = 0,2 м; .

Рис. 2.6

2.7. Определить отношение диаметров двух равнопрочных валов, передающих одинаковую мощность, если один делает , а другой .

Указание: мощность N = M·ω, где М – скручивающий момент; ω – частота вращения вала, рад/сек ( , где n – об/мин).

2.8. Наружный диаметр полого вала в 2 раза больше внутреннего. Определить размеры сечения вала, если он передает мощность 700 кВт при скорости вращения 100 об/мин, а наибольшие касательные напряжения в вале равны 60 МПа.

Замечание: скручивающий момент , где N – мощность, кВт; n – об/мин.

2.9. Стальной вал сплошного сечения передает мощность N = 60 кВт. Частота вращения вала n = 240 об/мин. Определить диаметр вала из расчета на прочность и жесткость, если МПа, а допускаемый угол закручивания [φ] = 1˚ (длина вала 1м, модуль сдвига МПа).

Указание: , где М – скручивающий момент, Н·м; N – мощность, кВт; n – об/мин.

2.10. Сплошной вал радиусом r усилен надетой на него трубой внутренним радиусом r и наружным R. Вал и труба изготовлены из одного материала и работают как одно целое. Чему должно равняться отношение R/r, чтобы описанное усиление вала позволило увеличить его грузоподъемность, т.е. скручивающий момент, вдвое.

2.11. Сплошной вал диаметром 40 см заменяется полым валом, у которого внутренний диаметр составляет 60 % от наружного. Определить наружный диаметр полого вала при условии, что допускаемые касательные напряжения у них одинаковы.

2.12. Сплошной вал круглого сечения был запроектирован в предположении определенной скорости его вращения. Затем было решено повысить скорость в 20 раз. Как изменится диаметр вала после его пересчета при неизменных остальных данных.

Замечание: выражение скручивающего момента М через мощность N и количество оборотов вала n

, где N – мощность, кВт; n – об/мин.

2.13. Два вала одинаковой длины из одного и того же материала воспринимают один и тот же крутящий момент. Один вал полый, с отношением диаметров . Другой вал – сплошной с диаметром D₀. Определить отношение весов полого и сплошного вала, если они равнопрочны.

2.14.Полый стальной вал длиной 1,8 м нагружен по концам двумя парами сил с моментами М = 0,6 кНм. Определить наружный и внутренний диаметры вала, если угол закручивания не должен превосходить 2˚, а касательные напряжения - 70 Н/мм². Модуль сдвига для стали Н/мм².

2.15. Сплошной вал диаметром D = 12см передает постоянный вращающий момент М. Определить необходимые размеры поперечного сечения полого вала из того же материала, такой же длины, имеющего прочность, как у сплошного вала, а жесткость – в 1,5 раза большую.

2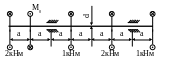 .16. Подобрать диаметр поперечного сечения вала (рис. 2.7) из условий прочности и жесткости, если а = 0,2м; МПа; ; МПа.

Рис. 2.7

2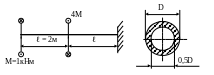 .17. Определить размеры поперечного сечения вала (рис. 2.8) из условий прочности и жесткости при ; [φ] = 2˚; МПа.

Рис. 2.8

2.18. Определить размер поперечного сечения вала (рис. 2.9) из условий прочности и жесткости, если а = 0,1м; b = 0,2м; ; ; МПа.

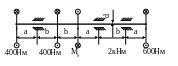
Рис. 2.9

2.19. Вал трубчатый (рис. 2.10). Определить размеры поперечного сечения вала (d и D), если M = 0,8 кНм; ; ; МПа; а = 1м.

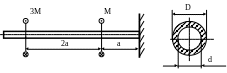
Рис. 2.10

2.20. Определить диаметры вала (рис. 2.11) и угол поворота сечения А по отношению к сечению В, если а = 1м; , М = 200 Нм; МПа.

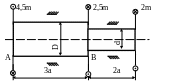
Рис. 2.11

2.21. Проверить прочность вала (рис. 2.12). Принять: d₁ = 60мм; d₂ = 40мм; М₁ = 1,5 кНм; М₂ = 2,5 кНм; М₃ = 5 кНм; .

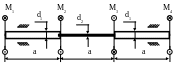
Рис. 2.12

2.22. Стальной круглый вал диаметром d = 16 мм испытан на кручение. При возрастании крутящего момента на угол закручивания между двумя сечениями, отстоящими друг от друга на расстоянии ℓ = 20см увеличивается на радиана. Вычислить модуль сдвига G и коэффициент Пуассона µ, если .

2.23. Стержень из малоуглеродистой стали диаметром 25мм удлиняется на 0,122мм на длине 20см при растяжении силой Р = 60 кН. Этот же стержень закручивается на угол 0,75˚ на длине 20см при нагружении скручивающим моментом М = 20кНсм. Найти упругие постоянные материала Е, G, µ.

2.24. Полый стальной вал с наружным диаметром D = 75мм и внутренним d = 50мм имеет длину ℓ = 1м. Он закручивается на 1˚ моментами М = 3,5 кНм. Определить максимальные касательные напряжения и модуль сдвига материала.

2.25. Сплошной вал диаметром d = 100 мм и длиной ℓ = 6000 мм закручен на угол 4˚. Чему равно наибольшее касательное напряжение, если МПа.

2.26. Определить τ_мах (максимальные касательные напряжения) и проверить прочность вала (рис. 2.13), если ; m = 1кНм; D = 60мм; а = 0,2м.

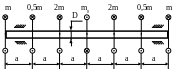
Рис. 2.13

2.27. При испытании на кручение стального образца длиной 20 см и диаметром 20 мм установлено, что при крутящем моменте М_к = 16,32кНсм угол закручивания равен 1,2˚. Предел упругости достигнут при М_к = 27кНсм. Определить модуль упругости при сдвиге и предел упругости при кручении.

2.28. Как изменится максимальное касательное напряжение и относительный угол закручивания, если сплошной вал заменить полым, вес которого на 20% меньше и отношение внутреннего диаметра к наружному равно 0,6.

2.29. Два вала, один из которых сплошной, а другой полый, имеют одинаковый вес и передают одинаковый крутящий момент. Длина валов и материал одинаковы. У какого вала наибольшие касательные напряжения будут больше и во сколько раз, если внутренний диаметр полого вала составляет 60% от наружного.

2.30. Наружный диаметр полого вала в два раза больше внутреннего. Этот вал на 20% легче сплошного вала, запроектированного при допускаемом напряжении на сдвиг . Чему равны наибольшие касательные напряжения в полом вале при одинаковых крутящих моментах.

2.31. Чтобы уменьшить вес сплошного круглого вала на 20%, его заменили полым, наружный диаметр которого в 2 раза больше внутреннего. Чему будут равны наибольшие касательные напряжения в полом вале, если в сплошном они были равны 6кН/см²?

2.32. Найти максимальные касательные напряжения на участках вала (рис. 2.14), проверить прочность вала, если ; m = 1кНм; d = 40мм; D = 60мм; а = 0,2м.

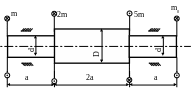
Рис. 2.14

2.33. Проверить прочность вала (рис. 2.15). Определить угол поворота сечения А по отношению к сечению В, если m = 1кНм; а = 1м; ; d = 40мм; D = 60мм; МПа.

Рис. 2.15

2.34. Для заданного вала (рис. 2.16) построить эпюры крутящего момента, угла закручивания φ и найти наибольшие касательные напряжения. Проверить прочность вала, если ; М = 2кНм; d = 2см; МПа; ℓ = 1м.

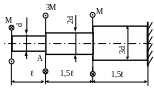
Рис. 2.16

2.35. Проверить прочность вала (рис. 2.17). Определить угол закручивания сечения А по отношению к сечению В. Принять: а = 2м; М₁ = 2кНм; М₂ = 5кНм; М₃ = 3кНм; МПа; d₁ = 20мм; d₂ = 40мм; .

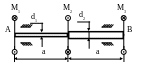
Рис. 2.17

2.36. Вал, защемленный с одного края, нагружен моментами М (рис. 2.18). Диаметры участков d₁ = 40мм; d₂ = 60мм. На 2-м участке максимальные касательные напряжения . Определить максимальные касательные напряжения на 1-м участке.

Рис. 2.18

2.37. Определить максимальное напряжение в сечении I – I и угол поворота этого сечения (рис. 2.19), если D₁ = 100мм; D₂ = 50мм; М₁ = 500 Нм; М₂ = 1500Нм; а = 20см; Н/мм².

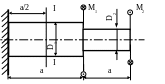
Рис. 2.19

2.38. Найти допустимое значение момента [M]. Определить угол закручивания φ_А сечения А (рис. 2.20), если d = 5см; а = 1м; ; МПа.

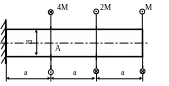
Рис. 2.20

2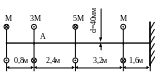 .39. Определить величину М и максимальные напряжения , если МПа, а угол закручивания сечения А (рис. 2.21) равен 1˚.

Рис. 2.21

2

М₂

М₁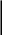

.40. Определить момент М₂ (рис. 2.22), если . Принять: МПа; а = 0,5м; d = 30мм; М₁ = 0,5кНм.

B

A

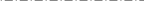
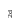
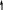
a

a

a

Рис. 2.22

2.41. Стальной ступенчатый вал (рис. 2.23) нагружен скручивающими моментами m₁, m₂, M. При каком значении момента М абсолютный угол закручивания в сечении «4» будет равен нулю, если а = 1м; m₁ = 20кНм; m₂ = 10кНм; d₃ = 5см; d₂ = 10см; d₁ = 20см; Н/мм².

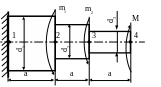
Рис. 2.23

2.42. Определить наибольший крутящий момент, который может быть приложен к стальному валу диаметром 10мм, если допускаемое напряжение не должно превосходить 15кН/см². Какова будет длина вала, если допускаемый угол закручивания [φ] = 2˚; кН/см².

2 .43. При заданном допускаемом напряжении [τ] = 20МПа определить величину момента М и угол закручивания φ сечения А (рис. 2.24).

Рис. 2.24

2.44. Для определения необходимого диаметра сплошного стального вала задано допускаемое касательное напряжение [τ] = 80МПа и допускаемый угол закручивания [φ] = 1˚ на длине вала, равной 1м. При каких величинах крутящего момента можно ограничиться определением диаметра только по допускаемому напряжению или только по допускаемому углу закручивания?

2.45. Два вала одинаковой длины и массы изготовлены из одного и того же материала. Один вал полый с отношением диаметров . Другой – сплошной диаметром D₀. Найти отношение крутящих моментов, которые могут быть приложены к валам при одинаковом допускаемом напряжении.

2.46. Определить величину крутящего момента М_к, при котором расчет круглого вала на прочность дает тот же диаметр, что и расчет на жесткость. Найти величину этого диаметра. Принять допускаемое касательное напряжение [τ] = 80 Н/мм², допускаемый относительный угол закручивания ˚/м, модуль сдвига Н/мм².