ГОУВПО «Воронежский государственный
технический университет»
А. А. Воропаев В.Н. Потапов Ф. Х. Томилов
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ:
ЗАДАЧИ ДЛЯ КОНТРОЛЬНЫХ РАБОТ
(ПРОСТОЕ ДЕФОРМИРОВАНИЕ)
Утверждено Редакционно-издательским советом
университета в качестве учебного пособия
Воронеж 2010
УДК 539.3/7
Сопротивление материалов: задачи для контрольных работ (простое деформирование): учеб. пособие / А.А. Воропаев, В.Н. Потапов, Ф.Х. Томилов; под ред. А.А. Воропаева. Воронеж: ГОУВПО «Воронежский государственный технический университет», 2010. 159 с.
В учебном пособии приведен набор стандартных и оригинальных задач по базовым разделам курса «Сопротивление материалов». Задачи предназначены для самостоятельной работы студентов при выполнении расчетно-проектировочных работ, а также при подготовке к контрольным работам, зачетам и экзаменам.
Учебное пособие подготовлено в электронном виде в текстовом редакторе MS Word XP и содержится в файле Сопромат10.doc.
Ил. 345. Библиогр.: 1 назв.
Рецензенты: кафедра теоретической и прикладной механики Воронежского государственного университета;
канд. техн. наук, доц. В.А. Рябцев
© Воропаев А.А., Потапов В.Н.,
Томилов Ф.Х., 2010
© Оформление. ГОУВПО «Воронежский
государственный технический универ-
ситет», 2010
ВВЕДЕНИЕ
В настоящем пособии рассматриваются типовые и оригинальные задачи для контрольных работ по курсу «Сопротивление материалов». Сборник охватывает основные разделы базовой части курса, предусмотренные типовой программой для технических вузов и содержит около двухсот задач, предназначенных для аудиторных занятий и самостоятельной работы студентов при выполнении домашних заданий в виде расчетно-проектировочных работ, а также при подготовке к контрольным работам, зачетам и экзаменам.
Отличительной особенностью настоящего пособия является использование универсального метода сил для решения статически неопределимых задач.
Условия некоторых задач сопровождаются несколькими расчетными схемами и, таким образом, общее число задач приближается к тремстам.
По всем темам курса в задачнике приведены задачи различной категории сложности, начиная от простейших, рассчитанных на знание основ курса и доступных практически всем студентам, и кончая задачами повышенной сложности, требующих от студентов хорошей подготовки и более глубоких знаний изучаемого курса. Задачи повышенной трудности отмечены звездочкой *.
Количество задач в сборнике значительно превышает то, которое может быть использовано в процессе изучения дисциплины. Сделано это с той целью, чтобы в зависимости от особенностей рабочей программы и постановки методики преподавания каждый преподаватель мог найти достаточное количество задач по основным разделам базовой части курса. Кроме того, большое количество простых задач, включенных в сборник, позволяет рассчитывать, что он вполне может быть использован при изучении курса студентами других технических специальностей вузов.
Тематика и схемы некоторых типовых задач заимствованы из учебной литературы, список которой приведен в конце пособия. Подавляющее же большинство задач являются оригинальными и составлены специально для настоящего сборника. При этом был использован и обобщен опыт многолетнего преподавания курса сопротивления материалов в Воронежском государственном техническом университете. По каждому из разделов приводятся задачи, посвященные различным видам расчетов на прочность и жесткость.
Задачи повышенной сложности предназначены для студентов, проявляющих повышенный интерес к предмету, и могут быть использованы при их подготовке к олимпиадам по сопротивлению материалов.
Настоящее пособие имеет целью облегчить студентам усвоение одной из наиболее сложных инженерообразующих дисциплин, приучить их к работе над книгой и развить в них навыки самостоятельного изучения материала. Книга призвана оказать помощь студентам в овладении методами решения типовых задач, связанных с расчетами элементов конструкций на прочность и жесткость в условиях статического нагружения.
1. Расчеты на прочность и жесткость при растяжении и
сжатии
1.1. Статически определимые системы
1.1.
Подобрать площади поперечных сечений
стержней и определить вертикальное
смещение точки А (рис. 1.1) (модуль упругости
материала стержней
МПа),
если
;
кН;
МПа.
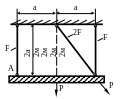
Рис. 1.1
1.2.
Определить диаметры стержней d1
и d2
и вертикальное перемещение точки А
(рис. 1.2), если
кН;
МПа;
МПа;
м;
;
˚;
β =60˚.
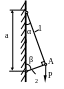
Рис. 1.2
1.3.
Подобрать диаметр подкоса d
(рис. 1.3), если
= 1 м;
;
.
Определить вертикальное перемещение
точки А.
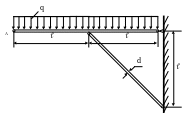
Рис. 1.3
1.4.
Подобрать площади поперечных сечений
стержней (рис. 1.4), если Р = 50 кН;
МПа. Определить вертикальное перемещение
узла С. Принять
= 1м;
МПа.
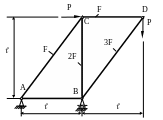
Рис. 1.4
1.5.
Дано: стержень АС – стальной, подкос BC
– деревянный (рис. 1.5). Допускаемое
напряжение для стали
МПа, для дерева
МПа; Р = 60 кН.
Подобрать
диаметр d
круглого поперечного сечения стального
стержня и сторону “
”
квадратного поперечного сечения
деревянного подкоса.
Найти полное перемещение узла С.
Рис. 1.5
1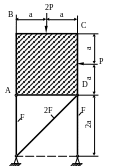
.6.
Абсолютно твердое тело АBCD
(рис. 1.6) закреплено с помощью стальных
стержней и нагружено двумя силами.
Подобрать площади поперечных сечений
стержней при допускаемом напряжении
для их материала
МПа. Определить горизонтальное смещение
точки D.
Числовые данные:
кН;
a
= 1м;
МПа.
Рис. 1.6
1.7.
Жесткий брус АВ (рис. 1.7) поддерживается
с помощью трех стальных стержней и
нагружен силой Р. Подобрать площади
поперечных сечений стержней при
допускаемом напряжении для их материала
МПа. Определить горизонтальное перемещение
точки А. Принять
кН;
a
= 1м; α = 45˚;
МПа.
Рис. 1.7
1
P
.
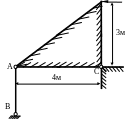
Рис. 1.8
1.9.
Проверить прочность стержней (рис. 1.9),
если
МПа. Определить вертикальное перемещение
точки А, если
;
МПа;
МПа;
Р = 20 кН; α = 45˚; β= 60˚;
= 1м.
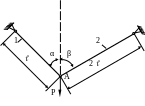
Рис. 1.9
1.10.
Конструкция состоящая из четырех
стержней (рис. 1.10), нагружена силой
.
Проверить прочность при допускаемом
напряжении для материала стержней
МПа. Принять а = 1м; F
= 3см2;
МПа.
Определить горизонтальное перемещение
узла В.
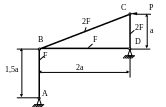
Рис. 1.10
1.11.
Проверить прочность стальных стержней
(рис. 1.11), если а = 1м; Р = 50кН; F
= 2 см2;
МПа. Определить вертикальное перемещение
точки А (
МПа).
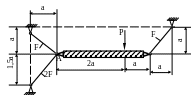
Рис. 1.11
1.12.
Произвести расчет на прочность штока
поршня компрессора (рис. 1.12), создающего
в цилиндре давление
МПа, если D
= 50мм; h
= 2мм; d
= 15 мм;
МПа.
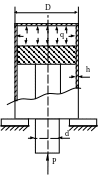
Рис. 1.12
1.13.
Абсолютно жесткое тело АВС (рис. 1.13)
закреплено с помощью шарнира С и стержня
BD.
Сила Р = 50 кН. Проверить прочность стержня
BD,
если допускаемое напряжение для его
материала
МПа. Найти горизонтальное смещение
точки В. Принять а = 1м; F
= 5см2;
E
= 105
МПа.
Рис. 1.13
1.14.
К двум тягам одинакового поперечного
сечения площадью F
= 1см2,
выполненным из одинакового материала
с модулем упругости
подвешен груз Р = 10 кН (рис. 1.14). Определить
перемещение точки подвеса груза, если
= 1мм. Проверить прочность стержней, если
МПа.
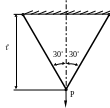
Рис. 1.14
1.15.
Жесткая балка АВ, деформацией которой
пренебрегаем, закреплена и нагружена,
как показано на рис 1.15. Стержень 1 –
стальной, сечением 10 см2,
стойка 2 – деревянная, сечением 10 ×
10 см, стержень 3 – медный, сечением 30
см2.
Определить опускание точки С. Проверить
прочность стержней, если
МПа;
МПа;
МПа.
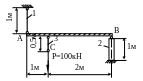
Рис. 1.15
1.16. Проверить прочность конструкции, состоящей из пяти стержней, шарнирно соединенных в узлах (рис. 1.16). Определить горизонтальное перемещение узла В. Принять Р = 40 кН; МПа; F = 1см2; а = 1м; МПа.
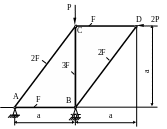Рис.
1.16
1.17. Проверить прочность стержней и найти горизонтальные смещения узла А (рис. 1.17), если Р = 40 кН; F = 3см2; а = 1м; МПа; МПа.
Рис. 1.17
1.18. Определить полное перемещение узла А (рис. 1.18). Проверить прочность стержней, если МПа; Р = 100 кН; 1 = 20см; 2 = 10см; F = 10см2; МПа.
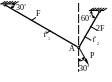
Рис. 1.18
1.19.
Найти вертикальное смещение точки С
(рис. 1.19). Проверить прочность стержней,
если
МПа; Р = 20 кН; а = 1м;
МПа; F1
= 1,5F2
= 2см2.
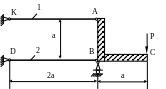
Рис. 1.19
1.20. АС – абсолютно жесткое тело, CD – стальной стержень (рис. 1.20). Проверить прочность и жесткость стержня, если известно, что напряжения не должны превышать 160 МПа, а вертикальное смещение точки А не должно быть больше 2 мм. Дано: а = 1м; Р = 20 кН; F = 3см2; МПа.
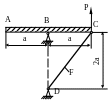
Рис. 1.20
1.21.
Жесткий брус нагружен силой Р и
удерживается наклонной стальной тягой
АВ круглого поперечного сечения диаметром
d
= 20мм (рис. 1.21). Определить допускаемую
нагрузку Р и вертикальное перемещение
точки приложения силы, если
;
.
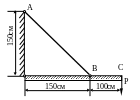
Рис. 1.21
1.22. Определить допускаемую нагрузку Р и горизонтальное смещение точки ее приложения (рис. 1.22).
Дано:
Тяга АВ – сталь, имеет диаметр d
= 20мм; а = 0,5м;
МПа;
.
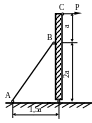
Рис. 1.22
1.23. Определить допускаемое значение момента М и вертикальное перемещение точки А (рис. 1.23), если = 1м, МПа; F = 30см2; МПа.
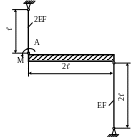
Рис. 1.23
1.24. Система трех стальных стержней нагружена силой Р (рис. 1.24). Определить допускаемое значение силы Р и горизонтальное смещение узла В. Числовые данные: МПа; F = 10см2; = 1,5м; МПа.
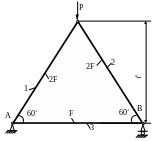
Рис. 1.24
1.25.
Определить допускаемое значение усилия
P
(рис. 1.25), если
;
;
= 1мм; α = 45˚;
МПа.
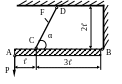
Рис. 1.25
1.26. Жесткая балка АВ (рис. 1.26) поддерживается с помощью трех стержней и нагружена силой Р. Определить допускаемое значение силы P при допускаемом напряжении для материала МПа. Найти вертикальное смещение точки В. Принять F = 3см2; а = 1м; МПа.
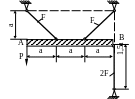
Рис. 1.26
1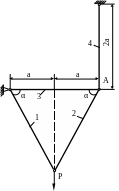
.27.
Стержневая система нагружена силой Р
(рис. 1.27). Материал стержней одинаков
(
МПа).
Площадь поперечного сечения стержней
F
= 2см2.
Допускаемое напряжение для материала
стержней
МПа. Определить допускаемое значение
силы Р и вертикальное смещение узла А,
если α = 60˚; а = 1м.
Рис. 1.27
1.28.
Жесткий брус АВ (рис. 1.28) закреплен с
помощью трех стальных стержней и нагружен
силой Р. Определить допускаемое значение
силы P
при допускаемом напряжении для материала
стержней
МПа. Найти вертикальное смещение точки
А. Числовые данные: а = 1м; F
= 2см2;
МПа.
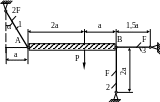
Рис. 1.28
1.2. Статически неопределимые системы
1
.29.
Определить площади поперечных сечений
стальных стержней (рис. 1.29), если Р = 200
кН;
МПа; а = 0,2м;
МПа.
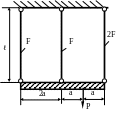
Рис. 1.29
1.30.
Жесткое (недеформируемое) тело А
поддерживается с помощью шарнира В и
двух стержней (рис. 1.30). Подобрать площади
поперечных сечений стержней, если
МПа;
МПа.
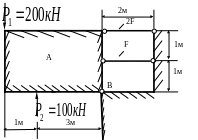
Рис. 1.30
1.31.Три стержня шарнирно соединены в одной точке и имеют одинаковое поперечного сечение (рис. 1.31). Определить площади поперечных сечений стержней, если Р =120 кН; МПа; α = 30˚; ℓ = 0,5м.
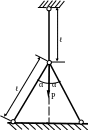
Рис. 1.31
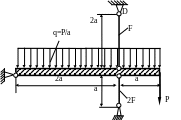1.32.Абсолютное
жесткая балка закреплена с помощью
стальных стержней (рис. 1.32). Вычислить
усилия в стержнях и определить из условия
прочности необходимую величину площади
сечения F.
Допускаемое напряжение на растяжение
Н/мм2;
допускаемое напряжение на сжатие
Н/мм2;
МПа;
а = 1м; Р = 10 кН.
Рис. 1.32
1.33.Определить площади поперечных сечений стальных стержней (рис. 1.33), если Р = 180 кН; МПа; а = 0,2м; МПа.
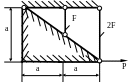
Рис. 1.33
1.34.Вычислить усилия в стержнях (рис. 1.34), считая, что они имеют одинаковое поперечного сечение и выполнены из одного материала. Подобрать площадь сечения наиболее нагруженного стержня при Р = 200 кН; МПа.
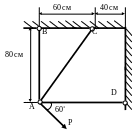
Рис. 1.34
1.35.Определить площади поперечных сечений стальных стержней (рис. 1.35), если Р = 180 кН; МПа; а = 0,2м; МПа.
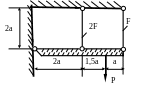
Рис. 1.35
1.36.Жесткое тело А поддерживается с помощью шарнира и двух стальных стержней (рис. 1.36). Определить площади поперечных сечений стержней, если Р = 180 кН; МПа; а = 0,4м; МПа.
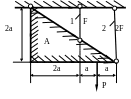
Рис. 1.36
1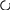
.37.Вычислить
усилия в стержнях плоской фермы (рис.
1.37), считая, что стержни выполнены из
одного материала и имеют одинаковое
поперечного сечение. Подобрать площадь
сечения по наиболее нагруженному стержню
при Р = 150 кН и допускаемом напряжении
МПа; ℓ = 1м.
D
Рис. 1.37
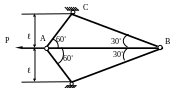
1.38.Определить
площади сечений стержней (рис. 1.38), если
q
= 10 кН/м; а = 1м;
МПа; α = 45˚; β= 30˚;
МПа.
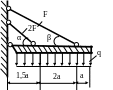
Рис. 1.38
1.39.Жесткое (недеформируемое) тело А закреплено с помощью шарнира и двух стержней (рис. 1.39). Определить площади поперечных сечений стержней, если Р = 180 кН; МПа; а = 0,4м; МПа.
Рис. 1.39
1.40.Подобрать
площади сечений стержней (рис. 1.40), если
стержень 1 - чугунный, 2 - медный, 3 –
стальной, Р = 120кН;
;
;
;
МПа;
МПа;
МПа.
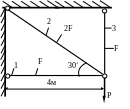
Рис. 1.40
1.41.Определить площади поперечных сечений стальных стержней (рис. 1.41), если Р = 200 кН; МПа; а = 0,3м; МПа.
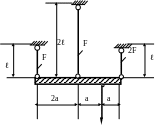
P
Рис. 1.41
1.42.Жесткое (недеформируемое) тело А поддерживается с помощью шарнира и двух стержней (рис. 1.42). Определить площади поперечных сечений стержней, если Р = 180 кН; МПа; а = 0,2м; МПа.
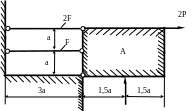
P
Рис. 1.42
1.43.Определить площади поперечных сечений стержней (рис. 1.43), если Р = 150 кН; МПа; МПа; α = 30˚; ℓ = 0,2м.
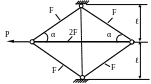
Рис. 1.43
1.44.Абсолютно
жесткая мачта CF
расчалена тросами и шарнирно оперта на
фундамент в точке С (рис. 1.44). Мачта
воспринимает равномерно распределенную
по ее высоте ветровую нагрузку
интенсивности q
= 0,5кН/м. Сечения тросов одинаковы,
материал тросов – сталь с модулем
упругости
МПа.
Подобрать сечения тросов при допускаемом
напряжении
МПа и вычислить горизонтальное смещение
точки F.
Тросы работают только на растяжение.
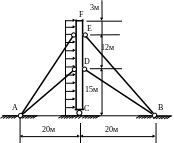
Рис. 1.44
1.45.Определить площади сечения тяг (рис. 1.45), если Р = 120 кН; МПа; а = 1м; МПа.
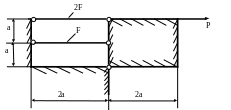
Рис. 1.45
1.46.Для
ступенчатого стержня, защемленного
обоими концами (рис. 1.46), построить эпюры
нормальных сил и найти смещение сечения
А-А. Подобрать площадь сечения из условия
прочности при допускаемых напряжениях
на растяжение
МПа,
на сжатие
МПа. Принять Р = 200 кН; q
= 200 кН/м; а = 0,5м.
Рис. 1.46
1.47.Жесткая балка поддерживается двумя стержнями (рис. 1.47). Определить площади сечения подвесок, если Р = 120 кН; МПа; а = 1м; α = 45˚; β = 60˚; МПа.
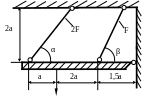
P
Рис. 1.47
1.48.Определить площади поперечных сечений стальных стержней (рис. 1.48), если Р = 180 кН; МПа; а = 0,2м; МПа.
Рис. 1.48
1.49.Определить площадь поперечного сечения стержня (рис. 1.49), если Р = 60кН; МПа; а = 0,2м.
Рис. 1.49
1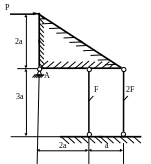
.50.Определить
напряжения в стальных стержнях (рис.
1.50), если Р = 50 кН; F
= 100мм2 ;
МПа;
а = 0,5м. Проверить прочность стержней,
если
МПа.
Рис. 1.50
1.51.Определить напряжения в стержнях из стали (рис. 1.51) и проверить прочность стержней, если Р = 50кН; F = 5см2 ; а = 1м; МПа; МПа.
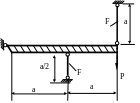
Рис. 1.51
1.52.Проверить прочность стальных стержней (рис. 1.52), если Р = 30кН; F = 2см2 ; ℓ = 1м; МПа; МПа; α =30˚.
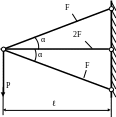
Рис. 1.52
1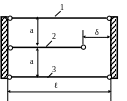
.53.Два
абсолютно жестких блока должны быть
соединены между собой тремя параллельными
упругими стержнями (рис. 1.53). Один стержень
оказался короче двух других на δ=
ℓ.
Вычислить напряжения в стержнях после
сборки (площади сечений стержней
одинаковы, модуль упругости
МПа).
Проверить прочность стержней, если
МПа.
Рис. 1.53
1.54.Определить напряжения в стальных стержнях (рис. 1.54), если Р = 150кН; МПа; МПа; F = 10см2 ; а = 1м. Проверить прочность стержней.
P
Рис. 1.54
1.55.Найти
монтажные напряжения и проверить
прочность стальных стержней (рис. 1.55),
если
МПа; F
= 10см2 ;
МПа.
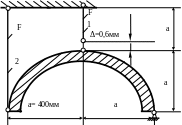
Рис. 1.55
1
.56.Квадратная
плита опирается на четыре симметрично
расположенных стойки одинакового
поперечного сечения (рис. 1.56), одинаковой
длины и из одинакового материала.
Определить усилия в стойках и проверить
их прочность, если: а = 2м; Р = 500кН;
МПа;
F
= 2000мм2 ;
МПа.
Рис. 1.56
1.57.Определить
напряжения в стержнях (рис. 1.57), если, Р
= 100кН; а = 0,3м; F
= 10см2 .
Проверить прочность стержней, если
;
МПа;
МПа.
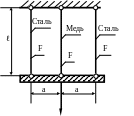
P
Рис. 1.57
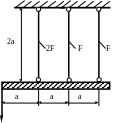
1.58.Определить напряжения в стальных стержнях системы (рис. 1.58), если а = 1м; Р = 20кН; F = 20см2 ; МПа; МПа. Проверить прочность стержней.
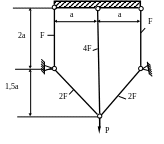
Рис. 1.58
1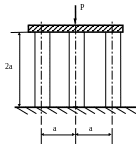
.59.Определить
напряжения в стойках (рис. 1.59), если
крайние стойки бетонные с размерами
квадратного поперечного сечения 30х30
см, средняя стойка – деревянная с
размерами прямоугольного поперечного
сечения 15х30 см. Проверить прочность
стоек, если Р =1620 кН; а = 0,5м;
;
МПа;
МПа.
Рис. 1.59
1.60.Жесткий брус подвешен на трех стальных стержнях (рис. 1.60) одинакового поперечного сечения площадью 20 см2 . Средний стержень выполнен короче проектного размера на Δ=0,5мм. Определить напряжения в стержнях после сборки конструкции. Проверить прочность стержней, если МПа; МПа.
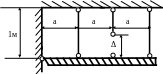
Рис. 1.60
1.61.Стальные
стержни 1 (рис. 1.61) выполнены длиннее
проектного размера на 1мм каждый и имеют
сечение
.
Стержни 2 – чугунные и имеют площадь
.
Определить напряжения в стержнях после
сборки (
МПа;
МПа).
Проверить прочность стержней, если
МПа;
МПа.
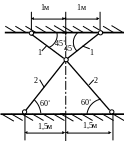
Рис. 1.61
1.62.Найти
напряжения в тросе, состоящем из
центральной стальной проволоки диаметром
5мм и девяти медных проволок диаметром
2,5мм, окружающих первую. Считать проволоки
параллельными. Растягивающее усилие в
тросе равно 5 кН. Проверить прочность
троса, если
МПа;
МПа;
МПа,
МПа.
1.63.Определить напряжения в стальных стержнях (рис. 1.62), если F = 10см2; а = 0.5м; Р = 30 кН; МПа; МПа. Проверить прочность стержней.
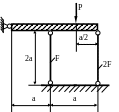
Рис. 1.62
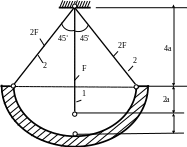1.64.Найти
монтажные напряжения и проверить
прочность стержней (рис. 1.63), если F
= 5см2 ;
МПа;
МПа, а=1м; Δ=1мм.
Δ
Рис. 1.63
1.65.Проверить прочность стержня (рис. 1.64), если МПа; МПа; а = 1,2м; F = 3см2 ; Δ = 0,15мм; Р = 40 кН.
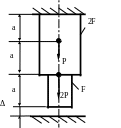
Рис. 1.64
1.66.Найти напряжения в стержнях после сборки (рис. 1.65) и проверить их прочность, если МПа; МПа; а = 1м; Δ = 0,4мм; F = 4см2 .
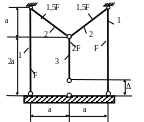
Рис. 1.65
1.67.Определить усилия в стержнях (рис. 1.66), если а = 1м; Р = 10 кН; F = 5см2 ; МПа; МПа. Проверить прочность стержней.
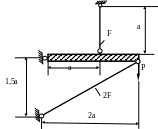
Рис. 1.66
1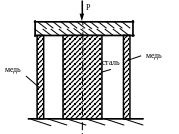
.68.Груз
Р = 50 кН передается через жесткую плиту
на сплошной стальной цилиндр (рис. 1.67)
площадью Fс
= 15см2
и полый медный цилиндр площадью Fм
= 20см2.
Определить напряжения в стальном и
медном цилиндрах и проверить их прочность,
если
МПа;
МПа;
МПа;
МПа.
Рис. 1.67
1.69.Определить усилия в стальных стержнях (рис. 1.68), если Р = 80 кН; F = 5см2 ; а = 0,5м; МПа; МПа. Проверить прочность стержней.
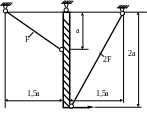
P
Рис. 1.68
1.70.Определить
напряжения в стержнях (рис. 1.69) при
нагреве системы на Δt
= 50˚С, если
МПа;
α
1/град.
Проверить прочность стержней, если
МПа.
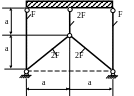
Рис. 1.69
1.71.Определить
усилия в стержнях (рис. 1.70), если
,
,
а = 1м; Р = 50 кН;
МПа;
F
= 40см2.
Проверить прочность стержней, если:
МПа.
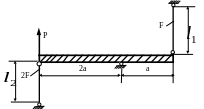
Рис. 1.70
1.72.Определить напряжения в стальных стержнях системы (рис. 1.71) и проверить их прочность, если Р = 150 кН; F = 5см2 ; а = 1м; МПа; МПа.
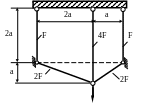
P
Рис. 1.71
1.73.Определить напряжения в стержнях (рис. 1.72), если Р = 100 кН; Н/мм2 ; МПа; а = 1м; ℓ = 0,8м; F = 10см2 . Проверить прочность стержней.
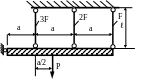
Рис. 1.72
1.74.Температура
системы (рис. 1.73) повысилась на Δt
=20˚С. Найти напряжения в стержнях и
проверить их прочность, если
МПа;
;
МПа;
МПа;
;
МПа.
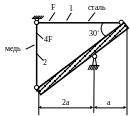
Рис. 1.73
1.75.Определить допускаемую нагрузку (рис. 1.74), если МПа; F = 30см2 ; а = 1м; МПа.
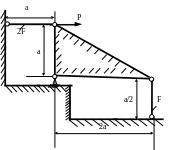
Рис. 1.74
1.76.Определить допускаемую нагрузку (рис. 1.75), если МПа; F = 40мм2 ; ℓ = 1м; а = 0,5м; МПа.
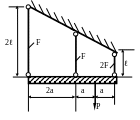
Рис. 1.75
1.77.Площади
стержней (рис. 1.76) одинаковы (F
= 2см2 ),
Δ
=10˚. Материал – сталь (
МПа;
α
).
Найти допускаемую нагрузку, если
МПа.
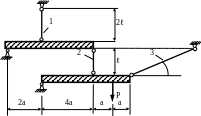
Рис. 1.76
1.78.Определить допускаемое значение нагрузки для системы стальных стержней (рис. 1.77), если МПа; F = 10см2 ; МПа; α =30˚; ℓ = 1м.
Рис. 1.77
1.79.Определить допускаемую нагрузку для системы из стальных стержней (рис. 1.78), если МПа; F = 20см2; а = 0,5м; МПа.
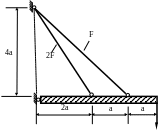
P
Рис. 1.78
1.80.Определить
наибольшую возможную нагрузку Р (рис.
1.79), если стержни 1,2 – стальные с площадью
сечений Fс
= 10см2 ,
а стержни 3,4 – медные с площадью сечений
Fм
= 20см2 .
Принять а = 0,2м; α =30˚; β= 60˚;
МПа;
МПа;
МПа,
МПа.
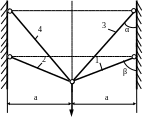
P
Рис. 1.79
1.81.Определить допускаемую нагрузку Р на стержень (рис. 1.80), если а = 0,5м; F = 30см2; МПа; МПа.
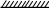
a
F
a
P
a
P
Рис. 1.80
1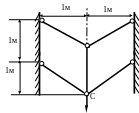
.82.Определить
опускание точки С системы из пяти
стальных стержней (рис. 1.81) одинакового
поперечного сечения площадью F
= 5см2,
если Р = 100 кН;
МПа.
P
Рис. 1.81