16. Условный экстремум
Рассмотрим функцию
(1)
при условии, что ее аргументы являются не независимыми переменными, а связаны между собой условием связи:
(2)
Пусть координаты точки
удовлетворяют уравнению (2).
Определение.
Функция (1) имеет в точке
условный минимум (максимум) при
условии связи (2), если существует такая
окрестность точки
,
что для любой точки
этой
окрестности (
),
координаты которой удовлетворяют
уравнению (2), выполняется неравенство
.
Иными словами, условный максимум (минимум)- это наибольшее (наименьшее) значение функции в точке по отношению не ко всем точкам из некоторой окрестности точки , а только к тем из них, которые связаны между собой условием связи.
Задачу об условном экстремуме функции можно решать методом исключения переменных. Этот метод состоит в том, что из уравнений условия связи одну переменную выражают через другую (если это возможно), подставляют найденное выражение в функцию и решают задачу об экстремуме функции одной переменной.
Пример 16.1. Найти
точки максимума и минимума функции
при условии
Решение. Из уравнения
выразим переменную
через переменную
и подставим полученное выражение
в функцию
.
Получим
или
Эта квадратичная функция имеет
единственный минимум при
.
При этом соответствующее значение
функции
Таким образом, (3;1)- точка условного
минимума.
Для отыскания условного экстремума в общем случае используется метод множителей Лагранжа.
Рассмотрим
задачу нахождения условного экстремума
функции
=
при наличии условия связи
= 0 в общем виде.
Рассмотрим функцию трех переменных
=
+
.
Эта
функция называется функцией
Лагранжа,
а
-множителем
Лагранжа.
Легко проверить, что необходимые условия
безусловного экстремума функции Лагранжа
имеют вид
(3)
Чтобы
найти достаточные условия экстремума,
следует определить знак полного
приращения D
=
–
функции
=
в точке
возможного экстремума. Но при наличии
связи
= 0 D
= D
,
где D
– полное приращение функции Лагранжа.
Поэтому достаточные условия безусловного
экстремума для функции Лагранжа будут
достаточными для условного экстремума
функции
.
Задача об условном экстремуме функции (1) при условиях связи (2) эквивалентна задаче об обычном экстремуме функции Лагранжа.
Пример 16.2. Найти условный экстремум функции
при
уравнении связи
.
Решение. Составим функцию Лагранжа
.
Обозначим
.
Найдём
стационарные точки этой функции
,
,
.
Решим систему уравнений
Решив
систему, находим
,
,
.
Имеем
,
,
,
.
=
2 – 2(-3) + 4 = 12 > 0, следовательно,
является точкой условного минимума.
Пример
16.3. Производственная функция (в денежном
выражении) имеет вид
(
-
количество единиц первого ресурса,
-
второго). Стоимость единицы первого
ресурса -5, второго -10 ден.ед. В силу
бюджетных ограничений на ресурсы, может
быть потрачено не более 600 ден. ед. В этих
условиях найти оптимальное для
производителя значение (
количества используемых ресурсов.
Решение.
В данном случае следует максимизировать
функцию
,
но при условии, что
В предыдущем разделе в задаче было
найдено оптимальное распределение
ресурсов в ситуации, когда ограничения
отсутствовали. Оказалось, что оптимальные
затраты на ресурсы равны
Можно показать, что в этом случае при
наличии ограничений на ресурсы следует
потратить всю возможную сумму.
Решаем
задачу максимизации функции
при условии, что
или
Составим
функцию Лагранжа
.
Частные
производные функции
равны
Приравнивая
их к нулю, найдем решение
Частные производные второго порядка
имеют вид:
.
Следовательно, (72;24)- точка условного
максимума.
Пример
16.4. Функция полезности имеет вид
Цена единицы первого блага равна 8,
второго – 16. На приобретение этих благ
может быть затрачена
сумма, равная 1000. Как следует распределить
эту сумму между двумя благами, чтобы
полезность от их приобретения была
наибольшей?
Решение. Найдем максимум функции
при
условии связи
Составим функцию Лагранжа
Найдем частные производные
Приравнивая
их к нулю, найдем решение,
Частные производные второго порядка
имеют вид:
.
Следовательно, (49,5;37,75)- точка условного
максимума.
Задачи для самостоятельной работы
1. Исследуйте на условный экстремум методом Лагранжа:
1.1.
Функцию
при
условии связи
1.2. Функцию
при условии связи
1.3.
Функцию
при
условии связи
1.4. Функцию
при
условии связи
1.5. Функцию
при
условии связи
1.6. Функцию
при
условии связи
1.7. Функцию
при условии связи
.
1.8. Функцию
при условии связи
.
2.
Заданы производственная функция (х-
количество единиц первого ресурса, у
–второго), цены единицы первого и второго
ресурсов, а также ограничения I
в сумме, которая может быть потрачена
на приобретение ресурсов (сумма
).
Найти величины используемых ресурсов
,
при которых фирма производитель получит
наибольшую прибыль: 2.1.
2.2.
3.
Потребитель имеет возможность потратить
сумму 1000 (ден. ед.) на приобретение х
единиц первого товара и у
единиц второго товара. Заданы функция
полезности
и
цены
единицы соответственно первого и второго
товаров. Найти значения
,
при которых полезность для потребителя
будет наибольшей.
3.1.
3.2.
17. НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ
ЗНАЧЕНИЯ ФУНКЦИИ
Если функция дифференцируема в ограниченной замкнутой области, то она достигает своего наибольшего (наименьшего) значения или в стационарной точке внутри области или в граничной точке области. Таким образом, для нахождения наибольшего (наименьшего) значения функции в замкнутой области, необходимо:
1) найти стационарные точки, расположенные в данной
области, вычислить значения функции в этих точках;
2) найти наибольшее и наименьшее значения функции
на линиях, образующих границу области;
3) из всех найденных значений выбрать наибольшее и наименьшее.
Пример 17.1. Найти наибольшее и наименьшее значения
функции
в области
,
(прямоугольнике).
Решение. 1) Найдем стационарные точки функции из
системы
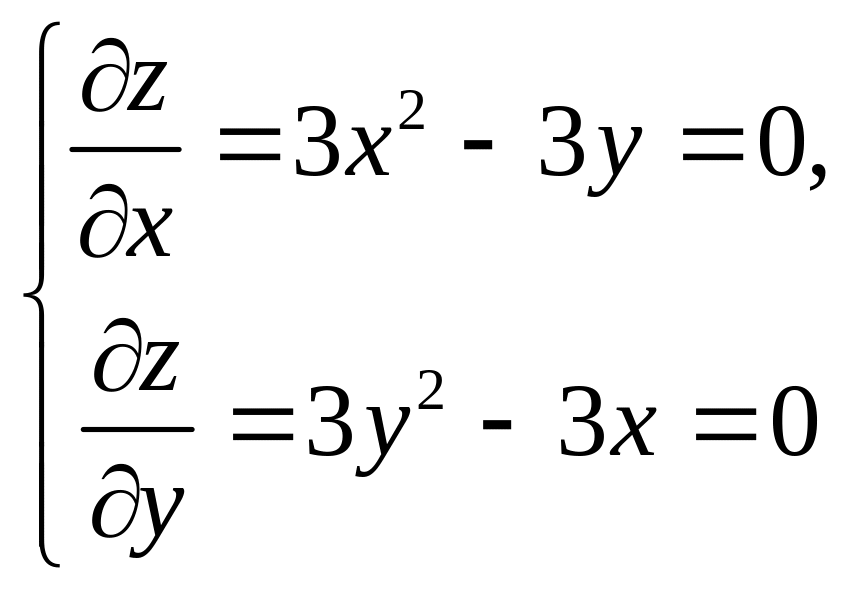Получаем две стационарных
точки
.
Значения функции в этих точках
Исследуем функцию на границах области:
а) При
имеем
.
Эта функция монотонно
возрастает и на концах
отрезка [-1,2] принимает значения
;
б) при
имеем
.
Найдем значения этой функции в стационарной
точке и на концах отрезка [-1,2]. Имеем
при
,
или в данной области, при
.
в) При
имеем
и
.
Функция монотонно возрастает от
до
.
г) При
имеем
и
при
.
Сравнивая все найденные значения функции, заключаем, что
в точке (2,-1);
в точках (1,1) и (0,-1).
Пример 2. Найти
наибольшее и наименьшее значения функции
в замкнутой области (D),
заданной неравенствами
,
,
.
Решение.
Изобразим
область (D);
она представляет собой треугольник с
вершинами A|(-1;
-2), B(-1;
5), C(6;
-2). Найдём стационарные точки.
,
.
Решим систему уравнений
Решением этой системы является x=1, y=2. Стационарная точка M(1;2) принадлежит области (D), так Рис. 5.
как её координаты удовлетворяют всем трём неравенствам, задающим треугольник (D). Найдём значение функции в этой точке: u(M) = 2 – 8 + 12 + 4 – 16 + 5 = –1.
Исследуем
функцию на границе
области
(D).
Граница
представляет собой объединение трёх
отрезков:
– отрезка BC,
– отрезка AB,
– отрезка AC.
1)
.
=
2x2
– 4x(4
– x)
+ 3(4 – x)2
+
4x
– 8(4–x)
+ 5 = 9x2
– 28x
+
+21.
Найдём
наибольшее и наименьшее значения функции
=9x2
– 28x
+ 21 на отрезке [–1; 6]. Имеем
18x
– 28; x
= 14/9 – стационарная точка функции
,
14/9 Î
Î
[–1; 6]. Обозначим N1(14/9
; 22/9 ). u(N1)
=
=
–34/9. Найдём значения
на концах отрезка [–1; 6]:
=
u(B)
= 58;
=
u(C)
= 177. Наибольшим из этих значений является
u(C)
= 177, наименьшим – u(N1)
= – 34/9.
2)
.
=
2 + 4y
+ 3y2
–
4 – 8y
+ 5 = 3y2
– 4y
+ 3.
Найдём
наибольшее и наименьшее значения функции
=
=3y2
– 4y
+ 3 на отрезке [–2; 5];
=
6y
– 4; y
= 2/3 – стационарная точка функции
,
принадлежащая отрезку [–2; 5]. Обозначим
N2(–1;
2/3). u(N2)
=
.
Найдём значения функции
на концах отрезка [– 2; 5]:
=
u(A)
= 23;
=
u(B)
= 58.
3)
.
=
2x2
+ 8x
+ 12 + 4x
+ 16 + 5 = 2x2
+ 12x
+ 33.
Обозначим
=
2x2
+ 12x
+ 33.
= 4x
+ 12. Стационарная точка x
= – 3 не принадлежит отрезку [–1; 6], поэтому
она нас не интересует. Значения
на концах отрезка
[–1;
6] были найдены ранее:
=
u(A)
= 23,
=
u(C)
= = 177. Сравнивая все полученные значения,
находим
=u(C)
= u(6;
–2) = 177,
=
u(M)
=
=u(1; 2) = – 1.
Задачи для самостоятельной работы
Найдите
наибольшее и наименьшее значения функции
в области (D),
заданной указанными неравенствами.
1.
2.
3.
;
4
5.
6.
;
7.
;
8.
;
ИНДИВИДУАЛЬНЫЕ ДОМАШНИЕ ЗАДАНИЯ
Вариант 1
1.
Найти частные производные функции
2.Составьте
уравнение касательной плоскости и
нормали к поверхности, заданной уравнением
F(x;
y;
z)=0
в указанной точке
.
3.Найдите точки экстремума функции .
4.Найдите условный экстремум функции при заданном уравнении связи.
5.Найдите
наибольшее и наименьшее значения функции
в области
,
заданной указанными неравенствами.
6.Найти
градиент функции
в точке М.
7.
Найти производную функции
в точке А
по направлению к точке В.
8.
Заданы производственная функция (х
-
количество единиц первого ресурса, у
– второго), цены единицы первого и
второго ресурсов, а также ограничения
I
в сумме, которая может быть потрачена
на приобретение ресурсов (сумма
).
Найти величины используемых ресурсов
,
при которых фирма производитель получит
наибольшую прибыль:
Вариант 2
1.Найти
частные производные функции
2.Составьте уравнение касательной плоскости и нормали к поверхности, заданной уравнением F(x; y; z)=0 в указанной точке .
3.Найдите точки экстремума функции .
4. Найдите условный экстремум функции при заданном уравнении связи.
5. Найдите наибольшее и наименьшее значения функции в области , заданной указанными неравенствами.
6. Найти градиент функции в точке М.
7. Найти производную функции в точке А по направлению к точке В.
8. Потребитель имеет возможность потратить сумму 1000 (ден. ед.) на приобретение х единиц первого товара и у единиц второго товара. Заданы функция полезности и цены единицы соответственно первого и второго товаров. Найти значения , при которых полезность для потребителя будет наибольшей:
Вариант 3
1.
Найти частные производные функции
2.Составьте уравнение касательной плоскости и нормали к поверхности, заданной уравнением F(x; y; z)=0 в указанной точке .
.
3. Найдите точки экстремума функции .
;
4. Найдите условный экстремум функции при заданном уравнении связи.
5. Найдите наибольшее и наименьшее значения функции в области , заданной указанными неравенствами.
6. Найти градиент функции в точке М.
7. Найти производную функции в точке А по направлению к точке В.
8.
Полезность от приобретения х
единиц первого блага и у
единиц второго блага имеет вид
Единица
первого блага стоит 2, а второго 3(ден.ед.).
На приобретение этих благ планируется
потратить 100 (ден.ед.). Как следует
распределить эту сумму, чтобы полезность
была наибольшей?
Вариант 4
1.
Найти частные производные функции
2. Составьте уравнение касательной плоскости и нормали к поверхности, заданной уравнением F(x; y; z)=0 в указанной точке .
.
3. Найдите точки экстремума функции .
;
4. Найдите условный экстремум функции при заданном уравнении связи.
5.Найдите
наибольшее и наименьшее значения функции
в области
,
заданной указанными неравенствами.
6. Найти градиент функции в точке М.
7.
Найти производную функции
в точке А
по направлению к точке В.
8.
Заданы производственная функция (х
-
количество единиц первого ресурса, у
–второго), цены единицы первого и второго
ресурсов, а также ограничения I
в сумме, которая может быть потрачена
на приобретение ресурсов (сумма
).
Найти вели чины используемых ресурсов
,
при которых фирма производитель получит
наибольшую прибыль:
Вариант 5
1.
Найти частные производные функции
2. Составьте уравнение касательной плоскости и нормали к поверхности, заданной уравнением F(x; y; z)=0 в указанной точке .
3. Найдите точки экстремума функции .
4. Найдите условный экстремум функции при заданном уравнении связи.
5.
Найдите наибольшее и наименьшее значения
функции
в области
,
заданной указанными неравенствами.
6. Найти градиент функции в точке М.
7.
Найти производную функции
в точке А
по направлению к точке В.
8. Потребитель имеет возможность потратить сумму 1000 (ден.ед.) на приобретение х единиц первого товара и у единиц второго товара. Заданы функция полезности и цены единицы соответственно первого и второго товаров. Найти значения , при которых полезность для потребителя будет наибольшей:
Вариант 6
1.
Найти частные производные функции
2. Составьте уравнение касательной плоскости и нормали к поверхности, заданной уравнением F(x; y; z)=0 в указанной точке .
3. Найдите точки экстремума функции .
4. Найдите условный экстремум функции при заданном уравнении связи.
.
5.
Найдите наибольшее и наименьшее значения
функции
в области
,
заданной указанными неравенствами.
6. Найти градиент функции в точке М.
7.
Найти производную функции
в точке А
по направлению к точке В.
8.
Заданы производственная функция (х-
количество единиц первого ресурса, у
–второго), цены единицы первого и второго
ресурсов, а также ограничения I
в сумме, которая может быть потрачена
на приобретение ресурсов (сумма
).
Найти величины используемых ресурсов
,
при которых фирма производитель получит
наибольшую прибыль:
Вариант 7
1.
Найти частные производные функции
2.
Составьте уравнение касательной
плоскости и нормали к поверхности,
заданной уравнением F(x;
y;
z)=0
в указанной точке
.
.
3. Найдите точки экстремума функции .
;
4. Найдите условный экстремум функции при заданном уравнении связи.
5. Найдите наибольшее и наименьшее значения функции в области , заданной указанными неравенствами.
6. Найти градиент функции в точке М.
7.
Найти производную функции
в точке А
по направлению к точке В.
8. Потребитель имеет возможность потратить сумму 221 (ден.ед.) на приобретение х единиц первого товара и у единиц второго товара. Заданы функция полезности и цены единицы соответственно первого и второго товаров. Найти значения , при которых полезность для потребителя будет наибольшей:
Вариант 8
1.
Найти частные производные функции
2.
Составьте уравнение касательной
плоскости и нормали к поверхности,
заданной уравнением F(x;
y;
z)=0
в указан точке
.
3. Найдите точки экстремума функции .
4. Найдите условный экстремум функции при заданном уравнении связи.
5. Найдите наибольшее и наименьшее значения функции в области , заданной указанными неравенствами.
6. Найти градиент функции в точке М.
7.
Найти производную функции
в точке А
по направлению к точке В.
8.
Заданы производственная функция (х-
количество единиц первого ресурса, у
–второго), цены единицы первого и второго
ресурсов, а также ограничения I
в сумме, которая может быть потрачена
на приобретение ресурсов (сумма
).
Найти величины используемых ресурсов
,
при которых фирма производитель получит
наибольшую прибыль:
Вариант 9
1.
Найти частные производные функции
2.
Составьте уравнение касательной
плоскости и нормали к поверхности,
заданной уравнением F(x;
y;
z)=0
в указанной точке
.
3. Найдите точки экстремума функции .
4. Найдите условный экстремум функции при заданном уравнении связи.
5. Найдите наибольшее и наименьшее значения функции в области , заданной указанными неравенствами.
6.
Найти градиент функции
в точке М.
7.
Найти производную функции
в точке А
по направлению к точке В.
8.
Заданы производственная функция (х-
количество единиц первого ресурса, у
–второго), цены единицы первого и второго
ресурсов, а также ограничения I
в сумме, которая может быть потрачена
на приобретение ресурсов (сумма
).
Найти величины используемых ресурсов
,
при которых фирма производитель получит
наибольшую прибыль:
Вариант 10
1.
Найти частные производные функции
2.
Составьте уравнение касательной
плоскости и нормали к поверхности,
заданной уравнением F(x;
y;
z)=0
в указанной точке
.
3. Найдите точки экстремума функции .
4. Найдите условный экстремум функции при заданном уравнении связи.
5. Найдите наибольшее и наименьшее значения функции в области , заданной указанными неравенствами.
6. Найти градиент функции в точке М.
7.
Найти производную функции
в точке А
по направлению к точке В.
8. Потребитель имеет возможность потратить сумму 174 (ден.ед.) на приобретение х единиц первого товара и у единиц второго товара. Заданы функция полезности и цены единицы соответственно первого и второго товаров. Найти значения , при которых полезность для потребителя будет наибольшей:
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Пискунов Н.С. Дифференциальное и интегральное исчисления/ Н.С. Пискунов.- М.: Наука, 2001. Т.1.- 250 с.
2. Сборник задач по математике для втузов. Ч.1. Линейная
алгебра и основы математического анализа. Под ред. А.В. Ефимова, Б.П.Демидовича.М.:Наука.1993.480 с.
3. Бутузов В.Ф. Математический анализ в вопросах и задачах. Функции нескольких переменных/ Бутузов В.Ф., Крутицкая Н.Ч., Медведев Г.Н., Шишкин А.А.- М.: Высш. Шк., 1988. 288с.
4. Зимина О.В. Высшая математика/ О.В. Зимина, А.И. Кириллов, Т.А. Сальникова.- М.: Физматлит, 2005.-368 с.
5. Рябушко А.П. Индивидуальные задания по высшей математике: учеб. пособие. В 4 ч. Ч.2. Комплексные числа. Неопределенные и определенные интегралы. Функции нескольких переменных. Обыкновенные дифференциальные уравнения/ А.П. Рябушко [и др.]. Минск:Выш. шк., 2007.-396 с.
6. Лунгу К.Н. Сборник задач по высшей математике. 1 курс/Лунгу К.Н., Письменный Д.Т. Федин С.Н., Шевченко Ю.А.-М.: Рольф, 2001.-576 с.
7. Красс М.С. Математика для экономистов: Учеб. пособие/ Красс М.С. , Чупрынов Б.П.- СПб.: Питер, 2009.-464с.
8. Кремер Н.Ш. Высшая математика для экономических специальностей: учебник и практикум/Н. Ш. Кремер, Б.П. Путко, И.М. Тришин, М.Н. Фридман; под ред. Н.Ш. Кремера.-М.: Изд. Юрайт; Высшее образование, 2010.-909 с.
СОДЕРЖАНИЕ
|
Введение………………………………………………… |
1 |
1. |
Основные определения………………………………... |
2 |
2. |
Линии и поверхности уровня………………………….. |
5 |
3. |
Частное и полное приращения функции……………… |
6 |
4. |
Предел и непрерывность функции нескольких переменных……………………………………………... |
6 |
5. |
Частные производные функции нескольких переменных……………………………………………... |
11 |
6. |
Производная по направлению. Градиент……………... |
14 |
7. |
Полный дифференциал функции нескольких переменных……………………………………………... |
17 |
8. |
Применение полного дифференциала к приближенным вычислениям…………………………. |
19 |
9. |
Геометрический смысл полного дифференциала. Касательная плоскость и нормаль к поверхности…… |
20 |
10. |
Производные сложных функций……………………… |
22 |
11. |
Полный дифференциал сложной функции…………… |
25 |
12. |
Производная от функции заданной неявно…………... |
26 |
13. |
Частные производные различных порядков…………. |
28 |
14. |
Дифференциалы высших порядков…………………… |
31 |
15. |
Экстремумы функции двух переменных……………... |
33 |
16. |
Условный экстремум…………………………………... |
39 |
17. |
Наибольшее и наименьшее значения функции………. |
45 |
|
Индивидуальные домашние задания…………………. |
49 |
|
БИБЛИОГРАФИЧЕСКИЙ СПИСОК………………… |
59 |
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
для организации самостоятельной работы
по изучению раздела «Функции нескольких переменных»
курса «Математический анализ»
для студентов направления подготовки
бакалавров 080100 «Экономика»
очной формы обучения
Составители:
Глушко Елена Георгиевна
Максимова Екатерина Игоревна
В авторской редакции
Компьютерный набор Е.Г. Глушко
Подписано к изданию 23.07.14.
Уч.- изд. л. 3,7.
ФГБОУ ВПО «Воронежский государственный
технический университет»