
- •1. Основные определения
- •2. Линии и поверхности уровня
- •4. Предел и непрерывность функции
- •5. Частные производные функции нескольких
- •9. Геометрический смысл полного
- •10. Производные сложных функций
- •11. Полный дифференциал сложной функции
- •12. Производная от функции, заданной неявно
- •13. Частные производные различных порядков
- •15. Экстремумы функции двух переменных
- •16. Условный экстремум
- •394026 Воронеж, Московский просп., 14
15. Экстремумы функции двух переменных
Определение. Точка называется точкой
локального максимума
(минимума) функции
,
если существует такая
![]() окрестность
окрестность
![]() точки
,
что
точки
,
что
![]() для любой точки
для любой точки
![]() .
.
Точка называется точкой локального экстремума, если она является либо точкой локального максимума, либо точкой локального минимума.
Эти формулировки переносятся без изменения на функции любого числа переменных.
Теорема1 (необходимое
условие экстремума). Если
![]() - точка локального экстремума функции
,
имеющей непрерывные частные производные
- точка локального экстремума функции
,
имеющей непрерывные частные производные
![]() в этой точке, то
в этой точке, то
![]()
Эта теорема не является достаточной для исследования вопроса об экстремальных значениях функции, но позволяет находить эти значения в тех случаях, в которых мы заранее уверены в существовании максимума или минимума.
Точки,
в которых
![]() (или не существует) и
(или не существует) и
![]() (или не существует), называются критическими
точками
(или не существует), называются критическими
точками
функции .
Точки, в которых все частные производные первого порядка равны нулю, называются точками стационарности функции или стационарными точками.
Для исследования функции в критических точках установим достаточные условия экстремума функции двух переменных.
Теорема 2 (достаточные условия экстремума). Пусть в некоторой области, содержащей точку , функция имеет непрерывные частные производные до третьего порядка включительно, пусть, кроме того, точка
- стационарная, то есть
Обозначим
![]()
и
![]() .
Тогда:
.
Тогда:
если
 ,
то в точке
функция
имеет минимум;
,
то в точке
функция
имеет минимум;если
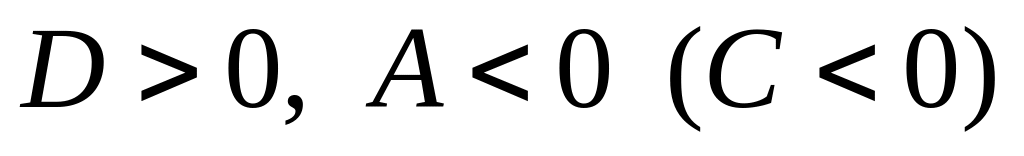 ,
то в точке
функция
имеет максимум;
,
то в точке
функция
имеет максимум;если
 ,
то экстремума в точке
нет;
,
то экстремума в точке
нет;если
 ,
то экстремум в этой точке может быть и
,
то экстремум в этой точке может быть и
может не быть (требуется дальнейшее исследование).
Пример 15.1. Найти
локальные экстремумы функции
![]() в области
в области
![]()
Решение. Найдем
![]() Решив
Решив
систему уравнений получим
получим
стационарную точку
![]() ,
то есть
,
то есть
![]() .
В этой точке выполнены необходимые
условия экстремума. Найдем вторые
частные производные
.
В этой точке выполнены необходимые
условия экстремума. Найдем вторые
частные производные
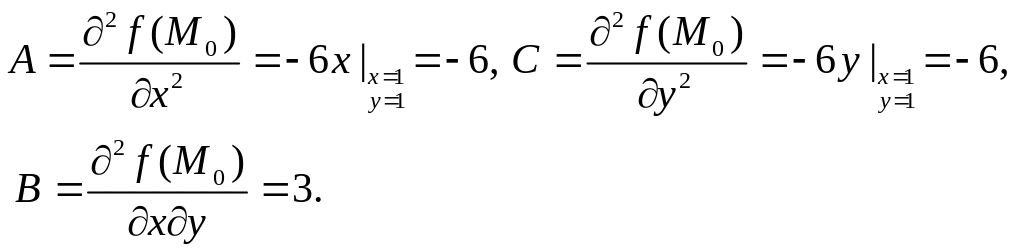
Вычислим
![]() .
Так как
.
Так как
![]() ,
то точка
является точкой локального максимума.
,
то точка
является точкой локального максимума.
Пример 15.2. Найти точки экстремума функции
![]() .
.
Решение.
Найдём
стационарные точки функции
![]() ,
,
![]() .
Решим систему уравнений
.
Решим систему уравнений
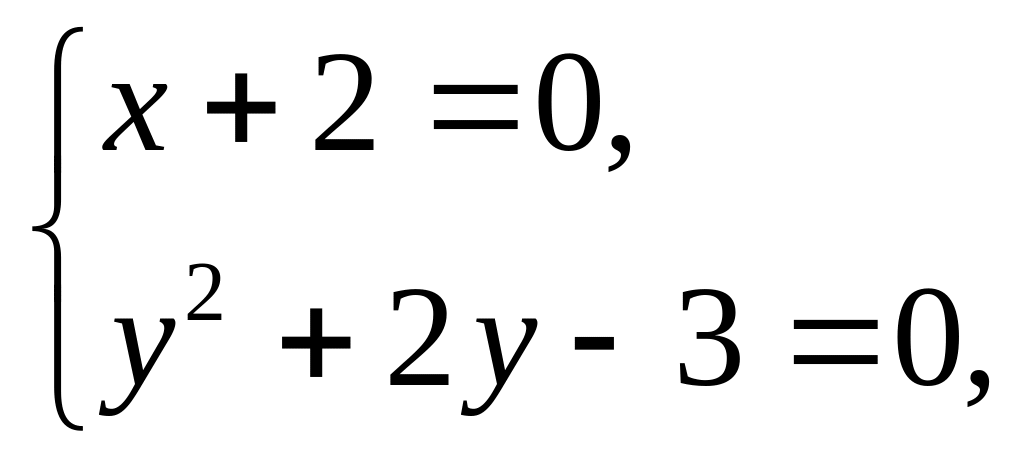
![]()
Решением системы являются точки M1(-2; -3), M2(-2; 1). Исследуем эти стационарные точки на экстремум, для чего найдём частные производные второго порядка:
![]() ,
,
![]() ,
,
![]() .
.
Имеем
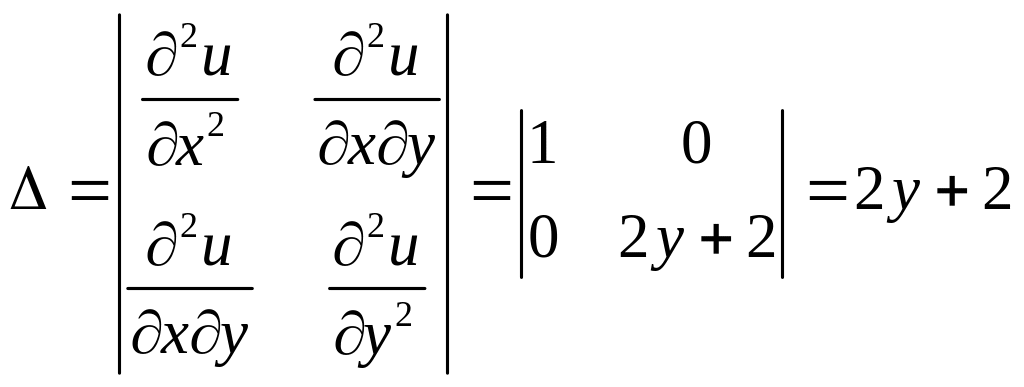 .
.
![]() ,
следовательно, M1(–2;
–3) не является точкой экстремума.
,
следовательно, M1(–2;
–3) не является точкой экстремума.
![]() ,
что говорит о том, что M2(–2;
1) является точкой экстремума. А так как
,
что говорит о том, что M2(–2;
1) является точкой экстремума. А так как
![]() ,
то заключаем, что M2
– точка минимума.
,
то заключаем, что M2
– точка минимума.
Пример
15.3. Пусть производится два вида продукции,
обозначим их количество через х
и у.
Пусть цены этой продукции, соответственно,
![]() и
и
![]() ,
а функция затрат
,
а функция затрат
![]() .
Тогда прибыль является функцией двух
переменных
.
Тогда прибыль является функцией двух
переменных
![]() Найти
значение максимальной прибыли.
Найти
значение максимальной прибыли.
Решение.
Частные производные функции
![]() равны
равны
![]() Приравнивая их к нулю, найдем решение
Приравнивая их к нулю, найдем решение
![]() Частные производные второго порядка
имеют вид:
Частные производные второго порядка
имеют вид:
![]()
![]()
![]() .
Следовательно, найденная точка определяет
локальный максимум функции прибыли,
который равен
.
Следовательно, найденная точка определяет
локальный максимум функции прибыли,
который равен
![]() .
.
Пример
15.4. Производственная функция (в денежном
выражении) имеет вид
![]() (
-
количество единиц первого ресурса,
-
второго). Стоимость единицы первого
ресурса -5, второго -10 ден.ед. Найти
максимальную прибыль при использовании
ресурсов.
(
-
количество единиц первого ресурса,
-
второго). Стоимость единицы первого
ресурса -5, второго -10 ден.ед. Найти
максимальную прибыль при использовании
ресурсов.
Решение.
Производственная функция в денежном
выражении равна доходу от использования
ресурсов. Издержки при этом равны
![]() Таким образом, функция прибыли равна
Таким образом, функция прибыли равна
![]() Требуется найти её максимум. Частные
производные функции
равны
Требуется найти её максимум. Частные
производные функции
равны
![]() Приравнивая их к нулю, найдем решение
Приравнивая их к нулю, найдем решение
![]() Частные производные второго порядка
имеют вид:
Частные производные второго порядка
имеют вид:
![]()
![]() .
.
Таким образом, найденная критическая точка есть точка максимума. Соответствующее значение прибыли равно 135 ден. ед.
Задачи для самостоятельной работы
Найти точки локального экстремума следующих функций двух переменных:
1.
![]() 2.
2.
![]()
3.
![]() 4.
4.
![]()
5.
![]() 6.
6.
![]()
7.
![]() 8.
8.
![]()
9.
![]() 10.
10.
![]()
11.
![]() .
12.
.
12.
![]() .
.
13.
![]() 14.
14.
![]()
15.
Цены
двух видов товаров равны, соответственно,
![]() и
и
![]() денежных единиц. Определить, при каких
количествах х
и у
продаж этих товаров прибыль будет
максимальной, если функция издержек
имеет вид
денежных единиц. Определить, при каких
количествах х
и у
продаж этих товаров прибыль будет
максимальной, если функция издержек
имеет вид
![]() .
.
16. Найти значения
величин используемых ресурсов
![]() ,
при которых фирма производитель получит
максимальную прибыль, если заданы
производственная функция
,
при которых фирма производитель получит
максимальную прибыль, если заданы
производственная функция
![]() и цены
и цены
![]() и
и
![]() не единицу первого и второго ресурсов:
не единицу первого и второго ресурсов:
15.1.
,
![]()
15.2.
![]() ,
,
![]()
