9. Геометрический смысл полного

ДИФФЕРЕНЦИАЛА. КАСАТЕЛЬНАЯ ПЛОСКОСТЬ И НОРМАЛЬ К ПОВЕРХНОСТИ

Подобно тому, как дифференциал функции одной переменной является приращением ординаты касательной, полный дифференциал функции двух переменных есть приращение аппликаты касательной плоскости.

Пусть функция имеет в точке частные производные первого порядка.

Определение. Касательной плоскостью к поверхности в ее точке (точке касания) называется плоскость, содержащая в себе все касательные к кривым, проведенным на поверхности через эту точку.

Определение. Нормалью к поверхности называется прямая перпендикулярная касательной плоскости и проходящая через точку касания.

Уравнение касательной плоскости к поверхности в точке имеет вид:

,

тогда из условия перпендикулярности прямой и плоскости, легко получить уравнения нормали:

Если уравнение поверхности задано неявно ,

то уравнение касательной плоскости имеет вид

,

а уравнения нормали:

Заметим, что полное приращение функции на

касательной плоскости имеет вид , то есть совпадает с полным дифференциалом функции .

Пример 9.1. Найти уравнения касательной плоскости и нормали к поверхности в точке .

Решение. Обозначим через левую часть уравнения поверхности, найдем частные производные и их значения

в точке :

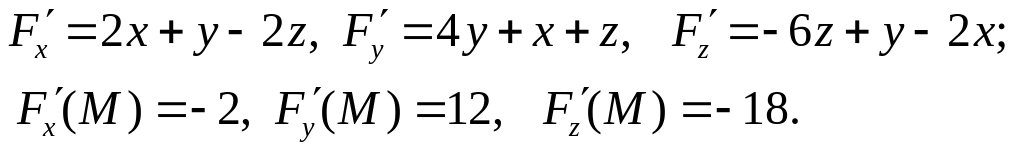
Подставляя найденные значения частных производных в уравнения касательной плоскости и нормали, получаем

или - уравнение касательной плоскости;

или -

уравнение нормали.

Задачи для самостоятельного решения

1. Найти уравнения касательной плоскости и нормали к поверхности в заданной точке М₀:

1.1. , (2,2,1). 1.2. , (1,2,5).

1.3. (4,3,4).

1.4.

1.5. 1.6.

1.7.

1.8.

10. Производные сложных функций

Пусть , тогда

является сложной функцией аргументов Предположим, что функции - дифференцируемые функции своих аргументов. Тогда формулы нахождения частных производных сложной функции по _{и по} имеют вид:

Пример10.1. Вычислить частные производные сложной функции

Решение.

=

=

Пример 10.2. Найти , если , , .

Решение. Имеем

, ,

, , , .

Отсюда получаем

,

.

Если функция , где функции зависят от одного аргумента : то функция фактически зависит от одной переменной и можно находить полную производную :

.

С учетом того, что , а функции зависят от одного аргумента , и , получаем формулу для нахождения полной производной:

.

Задачи для самостоятельной работы

1. Найти производные и функции , где

1.1.

1.2.

1.3.

1.4.

1.5.

1.6.

2. Найти сложной функции , где при .

2.1.

2.2.

2.3.

2.4.

2.5.

2.6. , где

11. Полный дифференциал сложной функции

Пусть . Найдем полный дифференциал сложной функции.

, но ,

, поэтому

или .

Мы показали, что выражения полного дифференциала

функции нескольких переменных (дифференциала первого порядка) сохраняет форму, следовательно, он обладает свойством инвариантности.

Задачи для самостоятельной работы

1. Найти , если :

1.1

1.2.

2. Найти , если

3. Выразить через и , если:

3.1.

3.2.

3.3.