
- •1. Основные определения
- •2. Линии и поверхности уровня
- •4. Предел и непрерывность функции
- •5. Частные производные функции нескольких
- •9. Геометрический смысл полного
- •10. Производные сложных функций
- •11. Полный дифференциал сложной функции
- •12. Производная от функции, заданной неявно
- •13. Частные производные различных порядков
- •15. Экстремумы функции двух переменных
- •16. Условный экстремум
- •394026 Воронеж, Московский просп., 14
4. Предел и непрерывность функции
НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Определение.
Окрестностью
радиуса
![]() точки
точки
![]() называется совокупность всех точек
называется совокупность всех точек
![]() ,
координаты которых удовлетворяют
неравенству
,
координаты которых удовлетворяют
неравенству
![]() ,
то есть совокупность точек, лежащих
внутри круга радиуса
,
с центром в точке
,
то есть совокупность точек, лежащих
внутри круга радиуса
,
с центром в точке
![]()
Пусть функция определенна в некоторой замкнутой области D плоскости , точка лежит в области D или на ее границе.
Определение.
Число
![]() называется пределом
функции
при стремлении точки
к точке
,
если для каждого числа
называется пределом
функции
при стремлении точки
к точке
,
если для каждого числа
![]() найдется такое число
найдется такое число
![]() ,
что для всех точек
из окрестности радиуса
точки
выполняется
неравенство
,
что для всех точек
из окрестности радиуса
точки
выполняется
неравенство
![]()
В
этом случае принято писать
![]()
Заметим, что предел функции двух переменных не должен зависеть от того, по какой линии точка стремится к точке .
Примеры.
1.
Найти предел функции
=
![]() в начале координат.
в начале координат.
Решение.
Поскольку, 0 £
£
![]() ,
а
®
0 при
,
а
®
0 при
®
0, то
![]() = 0.
= 0.
2.
Найти предел функции
![]() =
=
![]() в начале координат.
в начале координат.
Решение. Найдем предел функции по любой прямой =
=![]() ,
,
![]() ¹
0.
¹
0.
![]() =
=
![]() ®
0 при
®
0. Найдем теперь предел этой функции по
параболе
=
.
®
0 при
®
0. Найдем теперь предел этой функции по
параболе
=
.
![]() =
=
![]() =
=
![]() .
Следовательно, предела данная функция
в точке (0, 0) не имеет.
.
Следовательно, предела данная функция
в точке (0, 0) не имеет.
3.Вычислить
предел
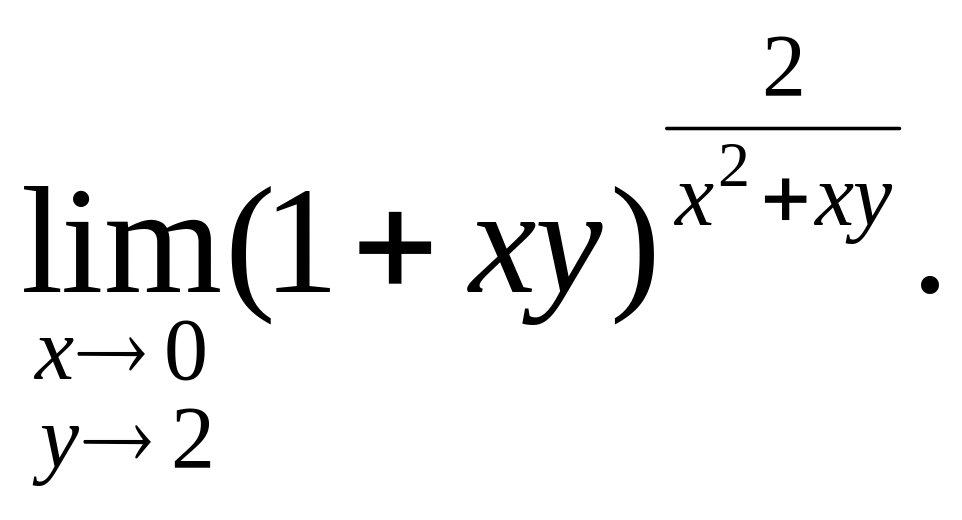
Решение.
Представим функцию в виде
![]() Так как
Так как
![]() при
при
![]() ,
то
,
то
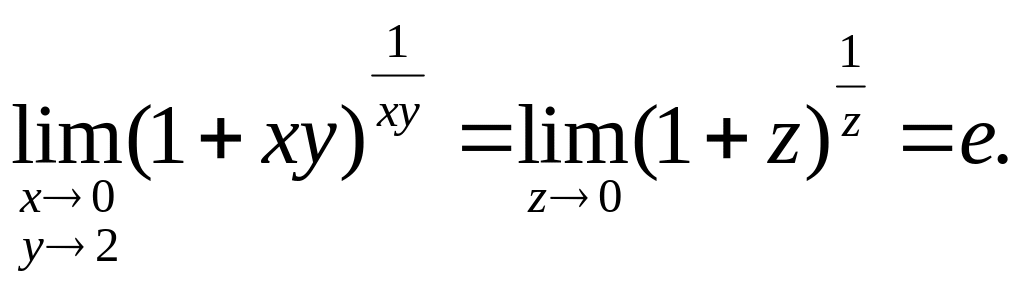
Далее,
![]() Поэтому искомый предел равен
Поэтому искомый предел равен
![]()
4.
Существует ли предел
![]() ?
?
Решение.
Пусть точка
стремится к точке
![]() по прямой
по прямой
![]() ,
проходящей через точку
,
проходящей через точку
![]() .
Тогда получим
.
Тогда получим
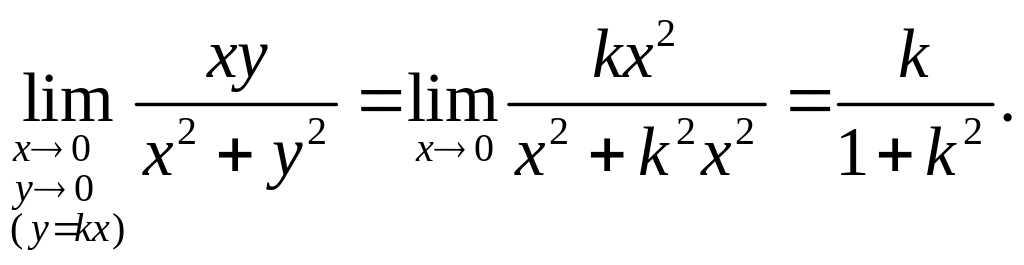 Таким
образом, приближаясь к точке
по различным прямым, соответствующим
разным значениям
,
получаем разные предельные значения.
Отсюда следует, что предел данной функции
в точке
не существует.
Таким
образом, приближаясь к точке
по различным прямым, соответствующим
разным значениям
,
получаем разные предельные значения.
Отсюда следует, что предел данной функции
в точке
не существует.
Определение.
Пусть точка
принадлежит области определения функции
.
Функция
называется непрерывной
в точке
,
если имеет место равенство
![]() причем точка
стремится к точке
произвольным образом, оставаясь в
области определения функции.
причем точка
стремится к точке
произвольным образом, оставаясь в
области определения функции.
Из определения следует, что для непрерывности функции в точке должны быть выполнены следующие условия:
функция определена в точке ;
существует предел
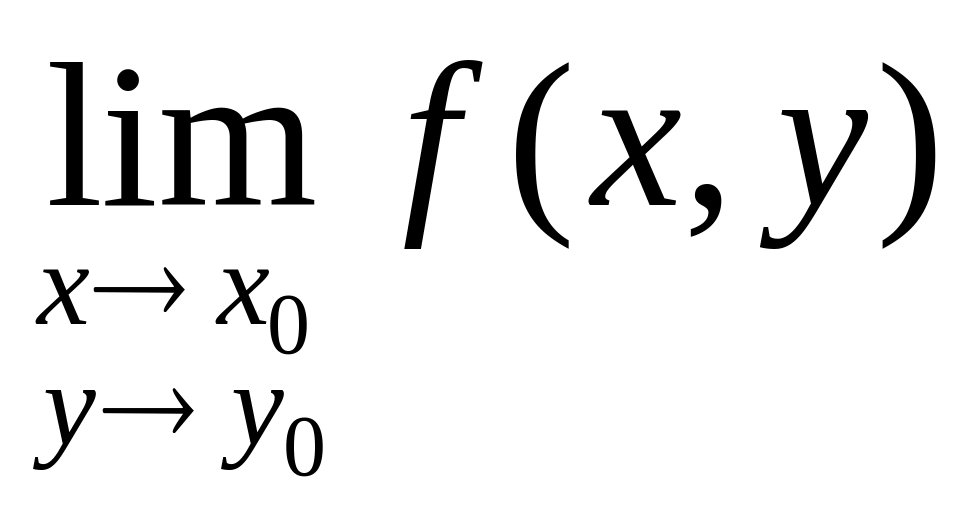 ;
;предел равен значению функции в точке
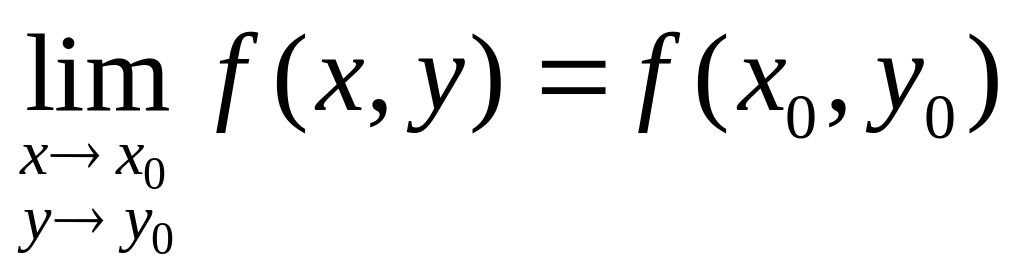 .
.
Если в некоторой точке не выполняется хотя бы одно из
условий (1-3), то точка называется точкой разрыва функции .
Приведем еще одно определение непрерывности функции в точке, эквивалентное данному выше:
Определение. Функция называется непрерывной в точке , если :
1) функция определена в этой точке;
2)
бесконечно малым приращениям
![]() соответствует бесконечно малое приращение
соответствует бесконечно малое приращение
![]()
Определение. Функция, непрерывная в каждой точке
некоторой области, называется непрерывной в этой области.
Примеры.
1. Исследовать непрерывность функции .
Решение. Найдем полное приращение функции
![]() .
Тогда
.
Тогда
![]() ,
то есть функция непрерывна.
,
то есть функция непрерывна.
2. Найти точки разрыва функции
![]() .
.
Решение. Данная функция не определена в тех точках, где
знаменатель
дроби равен нулю:
![]() ,
то есть функция не определена на прямой
,
то есть функция не определена на прямой
![]() В остальных точках плоскости функция
определена и непрерывна. Множество
точек разрыва данной функции есть прямая
Отметим, что в любой точке
В остальных точках плоскости функция
определена и непрерывна. Множество
точек разрыва данной функции есть прямая
Отметим, что в любой точке
![]() , лежащей на прямой
и не совпадающей с точкой
,
существует предел функции
, лежащей на прямой
и не совпадающей с точкой
,
существует предел функции
![]() Поэтому точки
при
Поэтому точки
при
![]() можно
назвать точками устранимого разрыва:
если положить
можно
назвать точками устранимого разрыва:
если положить
![]() ,
то функция станет непрерывной в точке
.
В точке
имеем
,
то функция станет непрерывной в точке
.
В точке
имеем
![]() ,
,
то есть - точка неустранимого разрыва данной функции.
Задачи для самостоятельной работы
Вычислить пределы:
1.1.
![]() 1.2.
1.2.
![]() 1.3.
1.3.
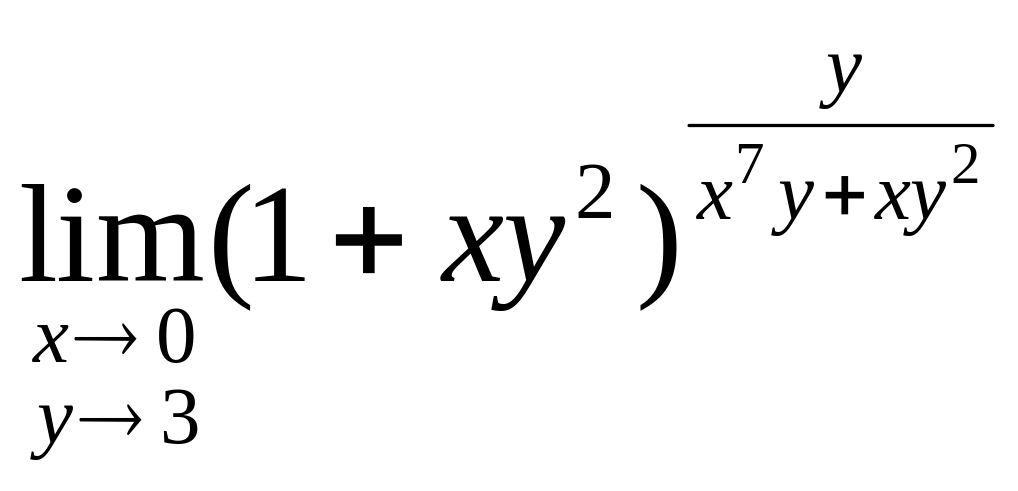 ;
;
1.4.
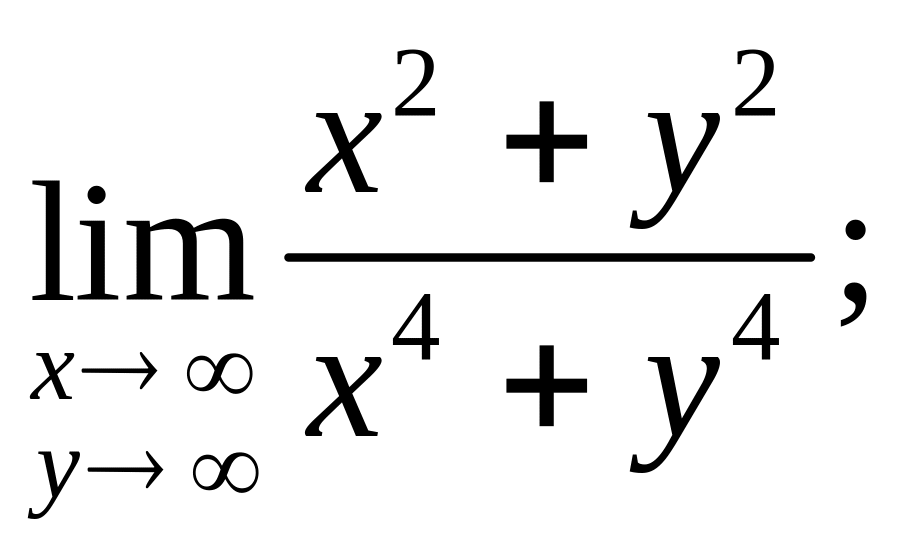 1.5.
1.5.
![]()
1.6.
![]() 1.7.
1.7.
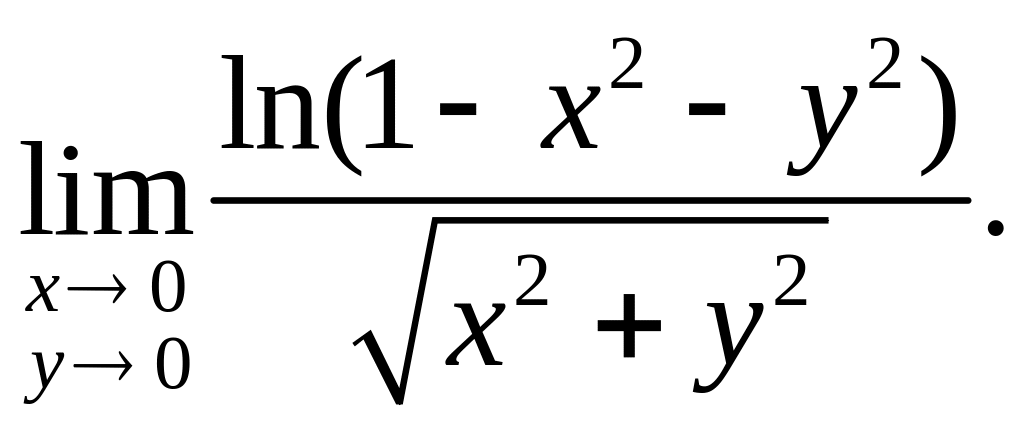
1.8.
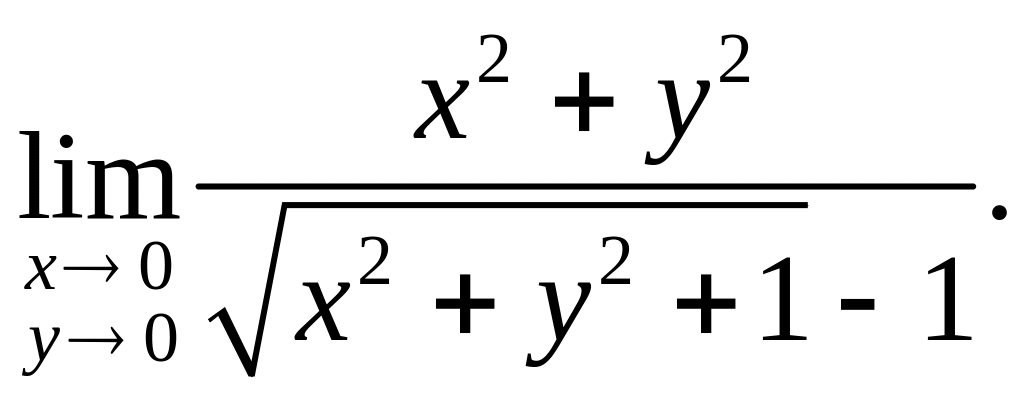
Докажите, что следующие пределы не существуют:
2.1
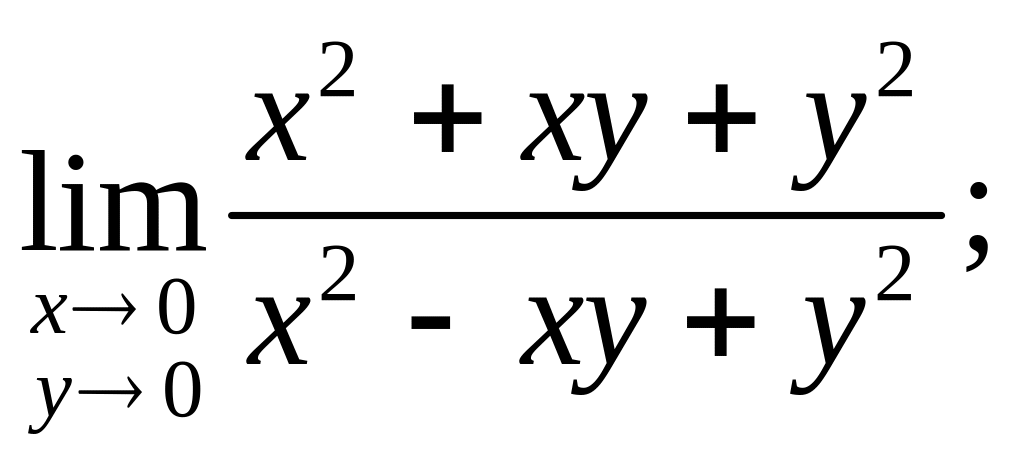 2.2.
2.2.
![]() 2.3.
2.3.
![]()
3.Найти точки разрыва следующих функций:
3.1.
![]() 3.2.
3.2.
![]()
3.3.
![]() ; 3.4.
; 3.4.
![]() 3.5.
3.5.
![]() ;
;
