ФГБОУ ВПО «Воронежский государственный
технический университет»
Кафедра высшей математики
и физико-математического моделирования
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
для организации самостоятельной работы
по изучению раздела «Функции нескольких переменных»
курса «Математический анализ»
для студентов направления подготовки
бакалавров 080100 «Экономика»
очной формы обучения
Воронеж 2014
Составители: канд. физ.-мат. наук Е.Г. Глушко,
канд. физ.-мат. наук Е.И. Максимова
УДК 517.9
Методические указания для организации самостоятельной работы по изучению раздела «Функции нескольких переменных» курса «Математический анализ» для студентов направления подготовки бакалавров 080100 «Экономика» очной формы обучения / ФГБОУ ВПО «Воронежский государственный технический университет»; сост. Е.Г. Глушко, Е.И. Максимова. Воронеж, 2014. 60 с.
В методических указаниях содержатся основные теоретические сведения по дифференциальному исчислению функций нескольких переменных. Приводится большое количество решенных типовых задач, задачи экономического содержания и задачи для самостоятельного решения.
Методические указания предназначены для организации самостоятельного изучения студентами первого курса раздела «Функции нескольких переменных» по курсу математического анализа.
Методические указания подготовлены на магнитном носителе в текстовом редакторе MS Word 2007 и содержатся в файле «ФНП. doc».
Ил. 5. Библиогр.: 8 назв.
Рецензент канд. физ.-мат. наук, доц. М.В. Юрьева
Ответственный за выпуск зав. кафедрой
д-р физ.-мат. наук, проф. И.Л. Батаронов
Издается по решению редакционно-издательского совета
Воронежского государственного технического университета
ФГБОУ ВПО «Воронежский государственный
технический университет», 2014
ВВЕДЕНИЕ
Многим явлениям, в том числе и экономическим, свойственна многофакторная зависимость. Исследование таких зависимостей потребовало введения понятия функции нескольких переменных.
Рассмотрим некоторые примеры функций нескольких переменных.
1.
Функция
,
где
-
постоянные числа, называется линейной.
Её можно рассматривать как сумму
линейных функций от переменных
.
2.
Функция
-
постоянные числа) называется квадратической.
3.
Одним из базовых понятий в экономической
теории является функция полезности.
Многомерный аналог этой функции - функция
,
выражающая полезность от n
приобретенных товаров. Чаще всего
встречаются следующие её виды:
а)
логарифмическая функция
,
где
б)
функция постоянной эластичности
,
где
4.
Для функции
переменных также обобщается понятие
производственной функции, выражающей
результат производственной деятельности
от обусловивших его факторов
.
Наиболее часто встречаются следующие
виды производственных функций (
-
величина общественного продукта,
-
затраты труда,
объём
производственных фондов). Положим для
простоты
.
а)
функция Кобба-Дугласа
б) функция с постоянной эластичностью замещения
.
1. Основные определения
Во многих вопросах экономической теории приходится иметь дело с функциями двух, трех и более переменных. В дальнейшем будем рассматривать функции двух переменных, что позволит использовать наглядную геометрическую иллюстрацию основных понятий.
Пример.
Решая уравнение сферы
относительно
при
,
получим
,
то есть
-
функция двух переменных. Определена
эта функция в круге
Определение.
Если каждой паре
значений двух независимых переменных
величин
и
из некоторой области их изменения
соответствует определенное значение
величины
,
то говорят, что
есть функция двух независимых переменных
и
,
определенная в области
и обозначают
.
Функцию двух переменных можно задать аналитически
или таблично.
Определение. Совокупность пар значений и , при которых определена функция называется областью определения или областью существования функции.
Пример 1.1. Найти и вычертить область определения функции:
1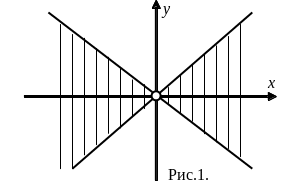
)
Решение. Функция
определена
при
и
.
При
получаем
.
Такому
двойному неравенству удовлетворяют
координаты точек плоскости, лежащие
ниже прямой
и выше прямой
при
При
получаем неравенство
,
справедливое для точек плоскости,
лежащих выше прямой
и ниже прямой
.
1.2.
Р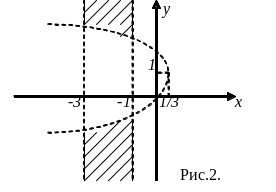
ешение.
Функция определена при
или
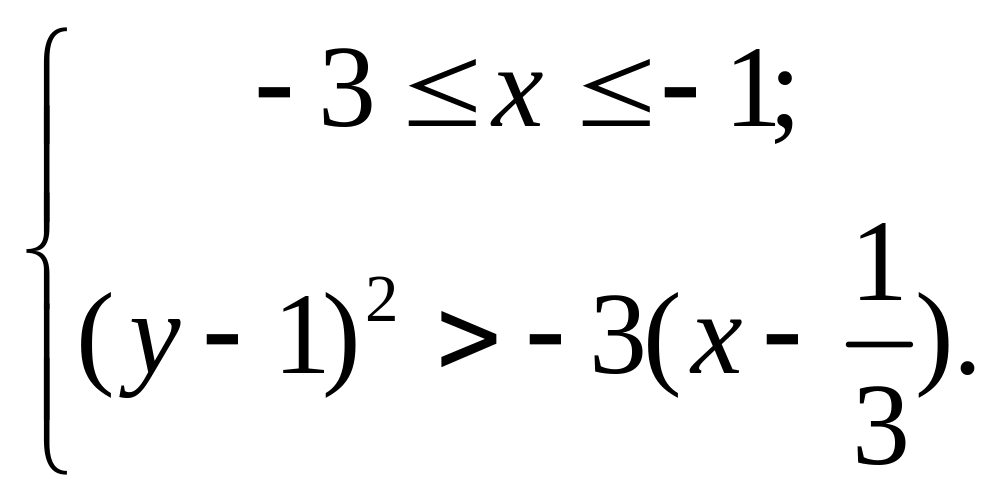
Таким образом, область определения функции двух переменных это совокупность точек плоскости или части плоскости, ограниченная линиями.
Геометрическим изображением
(графиком)
функции двух переменных
является поверхность в пространстве
.
Пример.
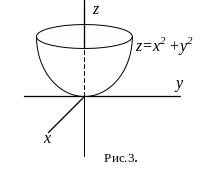
Графиком функции
является параболоид вращения (рис. 3).
Определение функции двух переменных легко обобщить на случай трех и более переменных.
Определение.
Если каждой рассматриваемой совокупности
значений переменных
соответствует определенное значение
переменной
,
то
называют функцией
независимых переменных и записывают
Геометрическое изображение функций трех и большего числа переменных не имеет простого геометрического смысла.
Задачи для самостоятельной работы
Найти и вычертить области определения функций двух переменных:
1.
.
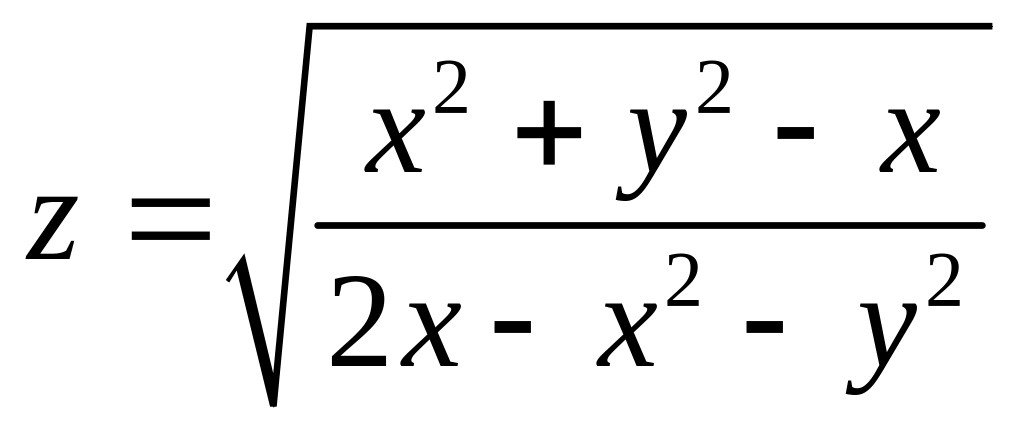2.
.
3.
.
4.
5.
6.
7.
8.
2. Линии и поверхности уровня
В
некоторых случаях можно получить
наглядное геометрическое представление
о характере изменения функции,
рассматривая ее линии
уровня
(или поверхности
уровня
).
Определение.
Линией
уровня
функции
называется множество всех точек плоскости
,
для которых данная функция имеет одно
и то же значение:
Число
С
в этом случае называется уровнем.
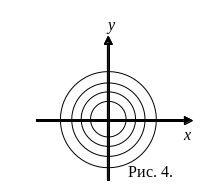
Пример.
Для функции
линиями уровня является семейство
концентрических окружностей
с центром в точке
(рис. 4).
Определение.
Поверхностью
уровня
функции
называется множество всех точек
пространства
,
для которых данная функция имеет одно
и то же значение.
Задачи и упражнения для самостоятельной работы
1.
Построить линии уровня функции
2.
Найти линии уровня в явном виде
2.1.
2.2.
2.3.
2.4.
2.5.
2.6.
3. ЧАСТНОЕ И ПОЛНОЕ ПРИРАЩЕНИЯ ФУНКЦИИ
Пусть
-
функция двух независимых переменных
и
.
Дадим переменной
приращение
,
оставляя
переменную неизменной. Разность
будем
называть частным
приращением функции
по переменной
.
Аналогично,
если
сохраняет постоянное значение, а
получает приращение
,
функция получает приращение, называемое
частным
приращением функции
по переменной
:
.
Если обе переменные и получили соответственно приращения и , то соответствующее приращение функции:
называется полным приращением функции .
Заметим, что полное приращение функции, вообще говоря, не равно сумме частных приращений этой функции
.