Часть 2. Расчеты на прочность, жесткость и устойчивость стержневых систем
1. РПР № 4. РАСЧЕТЫ НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ БАЛОК
1.1. Задания на рпр № 4
1.1.1. Задача № 1. Расчет консольной балки
Для заданной стальной консольной балки переменной жесткости (рис. 1.1) подобрать из расчета на прочность диаметры сплошного круглого сечения.
Рассчитать величину прогиба для крайнего
правого сечения и проверить жесткость
балки, если допускаемое значение прогиба
этого сечения
,
где l – длина балки.
В случае невыполнения условия жесткости
подобрать размер поперечного сечения
из этого условия. Принять
.
Значения нагрузок и размеров балки взять из табл.1.1.
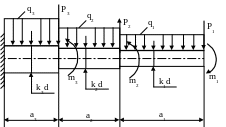
Рис. 1.1
1.1.2. Задача № 2. Расчет двухопорной балки
91
Р |
k3 |
1,4 |
1,4 |
1,4 |
1,4 |
1,4 |
1,4 |
1,4 |
1,3 |
1,3 |
1,3 |
1,3 |
1,4 |
1,4 |
1,4 |
1,4 |
1,3 |
1,3 |
k2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1,1 |
1,1 |
1,1 |
1,1 |
1,1 |
1,1 |
|
k1 |
0,6 |
0,7 |
0,8 |
0,5 |
0,6 |
0,7 |
0,8 |
0,5 |
0,6 |
0,7 |
0,8 |
0,5 |
0,6 |
0,7 |
0,8 |
0,5 |
0,6 |
|
а3 |
0,9а |
0,8а |
0,7а |
0,6а |
0,5а |
0,4а |
0,3а |
0,2а |
а |
0,9а |
0,8а |
0,7а |
0,6а |
0,5а |
0,4а |
0,3a |
0,2а |
|
а2 |
0,9а |
а |
0,2а |
0,3а |
0,4а |
0,5а |
0,6а |
0,7а |
0,8а |
0,9а |
а |
0,2а |
0,3а |
0,4а |
0,5а |
0,6a |
0,7а |
|
а1 |
а |
1,2а |
1,3а |
1,4а |
1,5а |
а |
1,2а |
1,3а |
1,4а |
1,5а |
1,3а |
1,2а |
1,3а |
1,4а |
1,5а |
a |
1,2а |
|
Н А Г Р У З К И |
m3 |
|
|
3qa2 |
|
|
3qa2 |
|
|
3qa2 |
|
|
3qa2 |
|
|
3qa2 |
|
|
m2 |
|
2qa2 |
|
|
2qa2 |
|
|
2qa2 |
|
|
2qa2 |
|
|
2qa2 |
|
|
2qa2 |
|
m1 |
qa2 |
|
|
qa2 |
|
|
qa2 |
|
|
qa2 |
|
|
qa2 |
|
|
qa2 |
|
|
P3 |
|
|
|
|
|
|
3qa |
3qa |
3qa |
|
|
|
|
|
|
3qa |
3qa |
|
P2 |
|
|
|
2qa |
2qa |
2qa |
|
|
|
|
|
|
2qa |
2qa |
2qa |
|
|
|
P1 |
qa |
qa |
qa |
|
|
|
|
|
|
qa |
qa |
qa |
|
|
|
|
|
|
q3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q2 |
|
|
|
|
|
|
|
|
|
2q |
2q |
2q |
2q |
2q |
2q |
2q |
2q |
|
q1 |
q |
q |
q |
q |
q |
q |
q |
q |
q |
|
|
|
|
|
|
|
|
|
№ вари-анта |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8
92 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|
А З М Е Р Ы
-
Р А З М Е Р Ы
k3
1,3
1,5
1,5
1,5
1,5
1,5
1,5
1,5
1,5
1,5
1,5
1,5
1,5
1,5
1,5
1,5
1,5
1,4
k2
1,1
1
1
1
1
1,1
1,1
1,1
1,1
1,2
1,2
1,2
1,2
1,3
1,3
1,3
1,3
1
k1
0,7
0,5
0,6
0,7
0,8
0,5
0,6
0,7
0,8
0,5
0,6
0,7
0,8
0,5
0,6
0,7
0,8
0,5
a3
a
0,9a
0,8a
0,7a
0,6a
0,5a
0,4a
0,3a
0,2a
a
0,9a
0,8a
0,7a
0,6a
0,4a
0,3a
0,2a
a
a2
0,8a
0,9a
a
0,2a
0,3a
0,4a
0,5a
0,6a
0,7a
0,8a
0,9a
a
0,2a
0,3a
0,4a
0,5a
0,6a
0,7a
a1
1,3a
1,4a
1,5a
a
1,2a
1,3a
1,4a
1,5a
a
1,2a
1,3a
1,4a
1,5a
a
1,2a
1,3a
1,4a
1,5a
Н А Г Р У З К И
m3
3qa2
3qa2
3qa2
3qa2
3qa2
3qa2
m2
2qa2
2qa2
2qa2
2qa2
2qa2
2qa2
m1
qa2
qa2
qa2
qa2
qa2
qa2
P3
3qa
3qa
3qa
3qa
-3qa
-3qa
P2
2qa
2qa
2qa
-2qa
-2qa
-2qa
P1
qa
qa
qa
-qa
-qa
-qa
q3
3q
3q
3q
3q
3q
3q
3q
3q
3q
q2
2q
q1
q
q
q
q
q
q
q
q
№ вари-анта
18
19
20
21
22
23
2
97
425
26
27
28
29
30
31
32
33
34
35
Определить методом Мора и проверить
способом Верещагина угол поворота
опорного сечения и прогиб у крайнего
сечения на одном из консольных участков
балки (номера сечений указаны в табл.
1.2).
Проверить жесткость балки в указанных
сечениях, если допускаемые значения
угла поворота и прогиба соответственно
равны
,
где l – длина балки.
Если жесткость балки не обеспечена,
подобрать номер прокатного двутавра
из расчета на жесткость.
Используя рассчитанные значения перемещений и эпюру изгибающих моментов, изобразить вид изогнутой оси балки.
Принять .
Значения нагрузок и размеров взять из табл. 1.2.
Рис. 1.2
94
93
7
-
№ №
сечений
1
4
1
4
1
4
1
4
1
4
1
4
1
4
1
4
1
3
2
3
2
3
2
3
2
3
2
3
2
3
2
3
2
3
Р А З М Е Р Ы
a3
0,9а
0,8а
0,7а
0,6а
0,5а
0,4а
0,3а
0
,2аа
0,9а
0,8а
0,7а
0,6а
0,5а
0,4а
0,3а
0,2а
a2
0,9а
а
0,2а
0,3а
0,4а
0,5а
0,6а
0,7а
0,8а
0,9а
а
0,2а
0,3а
0,4а
0,5а
0,6а
0,7а
a1
а
1,2а
1,3а
1,4а
1,5а
а
1,2а
1,3а
1,4а
1,5а
1,3а
1,2а
1,3а
1,4а
1,5а
а
1,2а
Н А Г Р У З К И
m3
3qa2
3qa2
3qa2
3qa2
3qa2
m2
2qa2
2qa2
2qa2
2qa2
2qa2
2qa2
m1
qa2
qa2
qa2
qa2
qa2
qa2
P3
3qa
3qa
3qa
3qa
3qa
P2
2qa
2qa
2qa
2qa
2qa
2qa
P1
qa
qa
qa
qa
qa
qa
q3
q2
2q
2q
2q
2q
2q
2q
2q
2q
q1
q
q
q
q
q
q
q
q
q
№ вари-
анта
1
2
3
4
5
6
7
95
8
9
10
11
12
13
14
15
16
17
-
№ №
сечений
4
1
4
1
4
1
4
1
4
1
4
1
4
1
4
1
4
1
2
3
2
3
2
3
2
3
2
3
2
3
2
3
2
3
2
3
Р А З М Е Р Ы
a3
а
0,9а
0,8а
0,7а
0,6а
0,5а
0,4а
0,3а
0,2а
а
0,9а
0,8а
0,7а
0,6а
0,4а
0,3а
0,2а
а
a2
0,8а
0,9а
а
0,2а
0,3а
0,4а
0,5а
0,6а
0,7а
0,8а
0,9а
а
0,2а
0,3а
0,4а
0,5а
0,6а
0,7а
a1
1,3а
1,4а
1,5а
а
1,2а
1,3а
1,4а
1,5а
а
1,2а
1,3а
1,4а
1,5а
а
1,2а
1,3а
1,4а
1,5а
Н А Г Р У З К И
m3
3qa2
3qa2
3qa2
3qa2
3qa2
3qa2
m2
2qa2
2qa2
2qa2
2qa2
2qa2
2qa2
m1
qa2
qa2
qa2
qa2
qa2
qa2
P3
3qa
3qa
3qa
3qa
-3qa
-3qa
P2
2qa
2qa
2qa
-2qa
-2qa
-2qa
P1
qa
qa
qa
-qa
-qa
-qa
q3
3q
3q
3q
3q
3q
3q
3q
3q
3q
q2
2q
q1
q
q
q
q
q
q
q
q
№ вари-
анта
18
19
20
21
22
2
96
324
25
26
27
28
29
30
31
32
33
34
35