4.2. Оценки параметров распределений случайных величин и процессов

Величина, которая в результате некоторого эксперимента с заранее непредсказуемым исходам каждый раз принимает одно из возможных значений, называется случайной. Пусть исход эксперимента (опыта, наблюдения) представляется некоторой случайной величиной . При N-кратном повторении эксперимента получают конкретный ряд значений x₁, …, x_N, который называется конечной выборкой объема N (выборочной совокупностью) из генеральной совокупности, содержащей все возможные значения случайной величины (N = ∞).

Для наиболее полной характеристики случайной величины (процесса) необходимо знать функцию ее распределения, устанав­ливающую связь между возможными значениями случайной величины в ее генеральной совокупности и соответствующими вероятностями появления каждого значения случайной величины. Существуют две основные формы функции распределения: интегральная и дифференциальная. Важными характеристик случайной величины являются математическое ожидание и дисперсия.

Интегральная функция F(x) = P{ <x} показывает, какая часть статистической совокупности лежит левее конкретного значения x случайной величины .Примерный график F(x) для непрерывной случайной величины изображена на рис. 4.1.

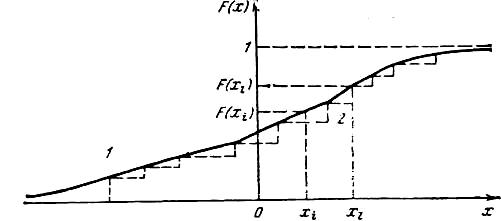
Рис. 4.1. Интегральная функция распределения F(x)

Для дискретной случайной величины он будет иметь ступенчатый вид. Основные свойства интегральной функции распределения следующие:

• F(x) — неотрицательная функция, т. е. при любых

;

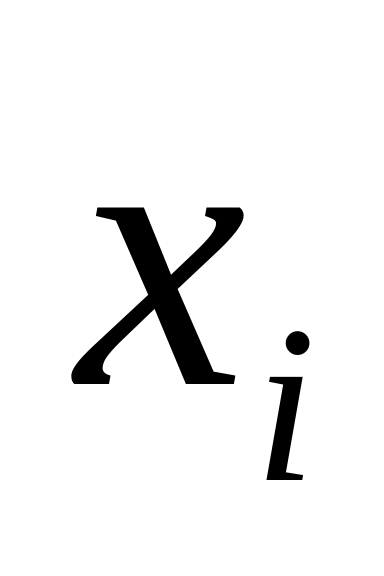
• F(х) — неубывающая функция, т. е. при x_i > x_l F(x_i) > F(x_l). Знак равенства может возникнуть, если в интервале (x_i, x_l) нет ни одного элемента статистической совокупности);

• lim F(x) = 0;(х -)

• lim F(x) = 1 ;(х ± )

Дифференциальная функция распределения φ(x) — это производная от интегральной функции распределения

.

Дифференциальную функцию распределения φ(x) называют также плотностью распределения непрерывной случайной величины. На рис. 4.2, а показан примерный вид дифференциальной кривой распределения непрерывной случайной величины, а на рис. 4.2, б дискретной случайной величины. На практике чаще используют дифференциальную форму записи закона распределения как более наглядную.

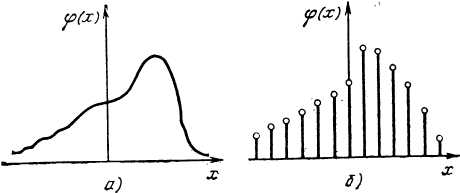
Рис. 4.2. Дифференциальная функция распределения φ(x):

а – для непрерывной случайной величины; б —для дискретной случайной величины.

Основные свойства дифференциальной функции распределения:

• функция 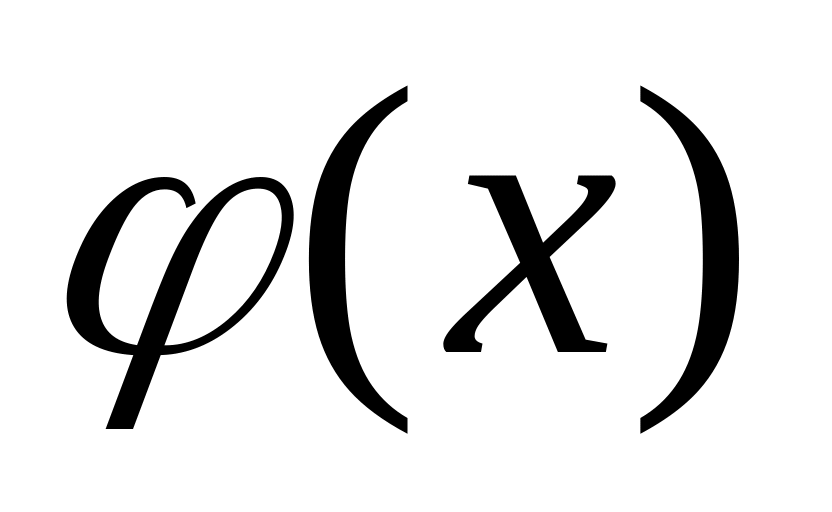— неотрицательная, т. е. при любых x ;

• .

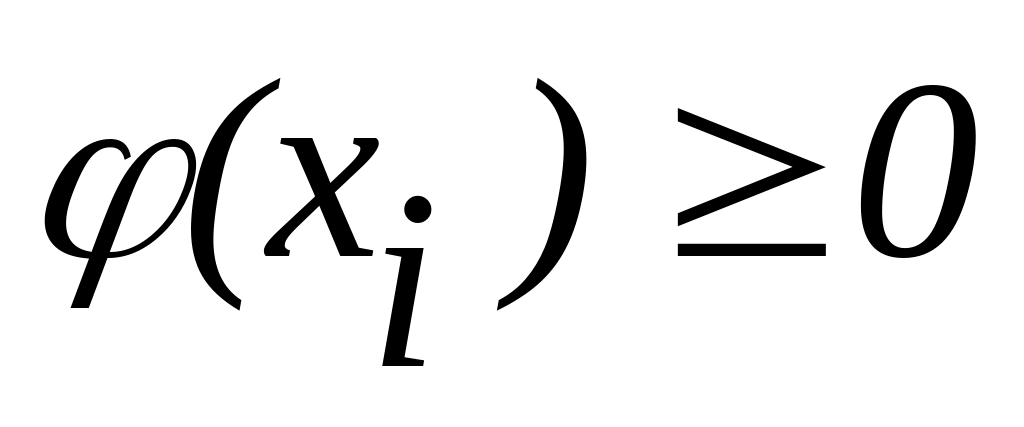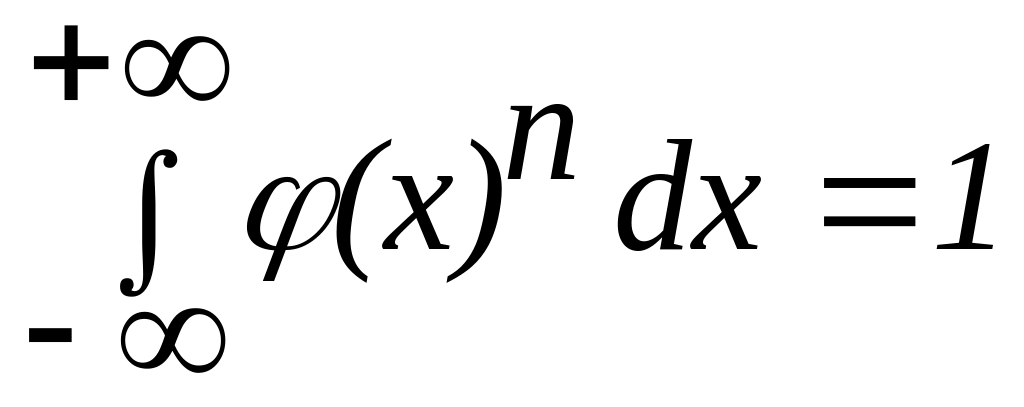Математическое ожидание случайной величины М_х характеризует положение некоторого среднего значения случайной величины из генеральной совокупности, воз­ле которого группируются возможные ее значения:

а) для непрерывной случайной величины

,

где φ(x) – дифференциальная функция распределения случайной величины ;

б) для дискретной случайной величины :

.

Геометрической интерпретацией математического ожидания яв­ляется абсцисса центра тяжести фигуры, ограниченной кривой распределения . Оценка математического ожидания опреде­ляется как среднее значение случайной величины для выбороч­ной совокупности:

где x_j — j-е значение случайной величины из выборочной сово­купности объемом N.

Степень рассеяния случайной величины относительно М_х характеризуется ее дисперсией.

Дисперсия генеральной совокупности случайной величины – есть математическое ожидание квадрата отклонений значений элементов генеральной совокупности от математического ожида­ния М_х случайной величины:

D_x=M{ (x-M_x) }.

Для непрерывной случайной величины генеральная дисперсия

Для случайной величины , представленной в виде ряда рас­пределения, генеральная дисперсия

где — абсцисса середины j-го интервала.

Дисперсия выборочной совокупности (выборочная дисперсия) является оценкой дисперсии и рассчитывается по ограниченному числу измерений случайной величины по формуле

где — среднее значение, являющееся оценкой математического ожидания М_х — i-e значение случайной величины из выборки объемом N.

Однако при малых выборках N пользуются несмещенной оценкой дисперсии

Оценка называется несмещенной, если ее математическое ожидание равно оцениваемому параметру при любом конечном, в том числе и малом объеме выборки N.

Для того чтобы знать, в ка­кой мере и в каком направлении влияет одна случайная перемен­ная на другую , т. е. оценить, как сильно они связаны, исполь­зуется коэффициент парной корреляции R_xy, асимптотически несмещенная оценка которого

где — i-e значение переменной ;

— i-е значение переменной ;

N — общее число наблюдений;

— среднее значение перемен­ной из выборочной совокупности;

— среднее значение пере­менной из выборочной совокупности;

s_x — выборочная оценка среднеквадратического отклонения переменной ;

s_y — выбороч­ная оценка среднеквадратического отклонения переменной ;

где s²_x и s²_y — соответственно выборочные дисперсии переменных и .

Коэффициент парной корреляции является показателем тесно­ты и направления корреляционной связи двух случайных перемен­ных, и его значение находится в пределах -1 ≤ R_xy ≤ +1.

При отсутствии корреляционной связи между двумя случайными переменными коэффициент парной корреляции R_xy = 0, в этом случае корреляционная связь между переменными и отсутствует. Если связь между двумя переменными линейная и функциональная, тогда R_XY = +1 или R_XY = –1.