Решение

Используя выражение, связывающее потенциальную энергию частицы с силой, действующей на неё, получим

.

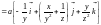Работа сил потенциального поля равна убыли потенциальной энергии

.

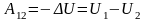По известным координатам точек M и N находим

, , .

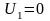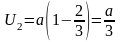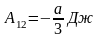Пример 9. Частица совершает перемещение в плоскости ХУ из точки с координатами (1,2) м в точку с координатами (2,3) м под действием силы 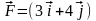Н. Определить работу данной силы.

Решение

Элементарная работа, совершаемая силой 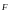при перемещении , равна скалярному произведению этих векторов

.

Работа при перемещении частицы из точки 1 в точку 2 определится интегрированием

.

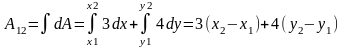Подставляя числовые значения, получим

.

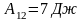Пример 10. Человек стоит на скамье Жуковского и держит в руках стержень, расположенный вертикально вдоль оси вращения скамейки. Стержень служит осью колеса, расположен- ного на верхнем конце стержня. Скамья неподвижна, колесо вращается с частотой ν^’= 10с^-1. Радиус колеса равен 20 см, его масса m = 3кг. Определить частоту вращения ν₁ скамьи, если человек повернёт стержень на угол 180⁰. Суммарный момент инерции человека и скамьи I = 6 кг·м².

Решение

Система “скамья – человек - колесо” является замкнутой и к ней можно применить закон сохранения момента импульса:

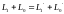, (1)

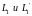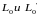где - моменты импульса системы “скамья - человек” до и после поворота колеса; - момент импульса колеса до и после поворота.

Учитывая что 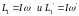, , 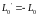, 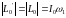уравнение (1) принимает вид

.

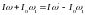Так как в исходном состоянии скамья Жуковского была в покое (ω = 0), то отсюда

,

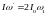и 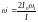. (2)

Выражая угловую скорость через частоту ν, получим

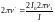, или .

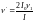Учитывая, что момент инерции колеса I₀ = mR² (тонкое кольцо), окончательно получим

.

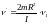После подстановки исходных данных

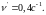
Пример 11. Если на верхний конец вертикально располо- женной спиральной пружины положить груз, то пружина сожмётся на Δl =3мм. На сколько сожмёт пружину тот же груз, упавший на конец пружины с высоты h = 8см?

Решение

В соответствии с законом сохранения механической энергии, полная энергия груза, падающего на пружину, равна энергии упругой деформации пружины при её сжатии. Полная энергия груза равна его потенциальной энергии U; при этом за нулевой уровень отсчёта потенциальной энергии примем положение сжатой пружины при падении груза (рис.1), тогда

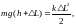(1)

где m – масса груза, g – ускорение свободного падения; k – жёсткость пружины.

Если груз положить на пружину (рис.2), то в соответствии с законом Гука запишем:

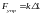. (2)

В состоянии равновесия сила упругости равна силе тяже- сти груза

,

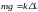о ткуда .

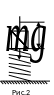
Подставляя полученное выражение для k в уравнение (1), получим:

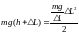. (3)

Уравнение (3) можно преобразовать к виду

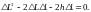
Тогда решение этого уравнения, удовлетворяющее физическому смыслу задачи (решением задачи будет являться лишь положительный корень), будет иметь вид:

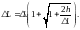
Выполняя вычисления, получим

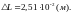
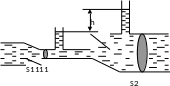Пример 12. Водомер представляет собой горизонтальную трубу переменного сечения, в которую впаяны две вертикальные манометрические трубки одинакового сечения (см. рис.). По трубе протекает вода. Пренебрегая вязкостью воды, определить её массовый расход, если разность уровней в манометрических трубках Δh = 8 см, а сечение трубы у оснований манометрических трубок соответственно равны S₁= 6 cм² и S₂ = 12 cм². Плотность воды ρ = 1 г/см³.