
- •Часть 2
- •Методические указания
- •Часть 2
- •Введение
- •Занятие № 15
- •Интегрирование дифференциальных
- •Биномов. Подстановки чебышева.
- •Подстановки эйлера
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятия № 16 приложения определенного интеграла
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 17 условный экстремум. Метод множителей лагранжа. Наибольшее и наименьшее значения.Функции в замкнутой области
- •Контрольные вопросы и задания
- •Примеры решения задач
- •17.3. Задачи и упражнения для самостоятельного решения
- •Занятие № 18 дифференциальные уравнения, приводящиеся к однородным
- •Основные понятия
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 19
- •Основные понятия
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 20
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 21 дифференциальнЫе уравнения, допускающие понижение порядка.
- •Основные понятия
- •I. Уравнения вида
- •II. Уравнения вида , явно
- •III. Уравнения вида , явно
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 22 Линейные дифференциальные уравнения высших порядков с постоянными коэффициентами со специальной правой частью
- •Основные понятия
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 23
- •Решение Систем дифференциальных уравнений (метод исключения)
- •Литература: [1], с. 103-107.
- •Основные понятия
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 24 Понятие о теории устойчивости ляпунова
- •Основные понятия
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 25. Приближенное решение дифференциальных уравнений
- •Контрольные вопросы и задания
- •Заключение
- •Библиографический список
- •Часть 2
- •В авторской редакции
Контрольные вопросы и задания
1. Какая система дифференциальных уравнений называется нормальной?
2. В чем состоит метод исключения неизвестных в нормальной системе?
3. Каков алгоритм метода исключения?
4. Какой метод решения систем более общий: метод характеристического уравнения или метод исключения неизвестных?
Примеры решения задач
Пример
1. Решить
систему
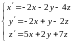 .
.
Решение.
В данной системе
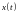 ,
,
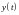 ,
,
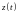 – неизвестные функции. Дифференцируем
первое уравнение системы по
:
– неизвестные функции. Дифференцируем
первое уравнение системы по
:
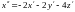 .
Вместо
и
.
Вместо
и
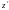 подставим их выражения из второго и
третьего уравнений системы. Тогда
подставим их выражения из второго и
третьего уравнений системы. Тогда
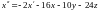 .
Полученное уравнение дифференцируем
по
,
а вместо
и
подставим их выражения из второго и
третьего уравнений системы:
.
Полученное уравнение дифференцируем
по
,
а вместо
и
подставим их выражения из второго и
третьего уравнений системы:
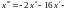
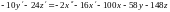 .
Составим новую систему:
.
Составим новую систему:
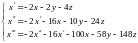 .
(6.3)
.
(6.3)
Из
этой системы исключим неизвестные
и
 .
Для этого используем первые два уравнения
системы (6.3), из которых, после преобразований,
находим
.
Для этого используем первые два уравнения
системы (6.3), из которых, после преобразований,
находим
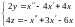 (6.4)
(6.4)
и
эти выражения подставим в третье
уравнение системы (6.3) и получим однородное
дифференциальное уравнение третьего
порядка с постоянными коэффициентами
относительно функции
:
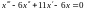 .
Решаем соответствующее характеристическое
уравнение
.
Решаем соответствующее характеристическое
уравнение
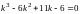 и находим
и находим
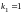 ,
,
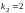 ,
,
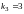 .
Следовательно, общее решение
.
Следовательно, общее решение
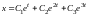 .
Далее находим производные
.
Далее находим производные
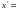
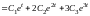 ,
,
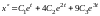 и подставляем
,
и подставляем
,
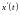 ,
,
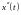 в систему (6.4). Получаем
в систему (6.4). Получаем
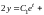
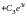 ,
,
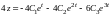 .
В итоге, общее решение исходной системы
имеет следующий вид:
.
В итоге, общее решение исходной системы
имеет следующий вид:
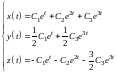 .
.
Пример
2. Решить
систему
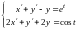 при данных начальных условиях:
при данных начальных условиях:
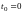 ,
,
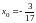 ,
,
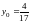 .
.
Решение. Сначала приводим систему к нормальному виду
 .
.
Первое
уравнение дифференцируем по
,
после чего вместо
подставим выражение из второго уравнения
системы:
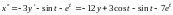 .
Из этого уравнения и первого уравнения
исходной системы составим новую систему
.
Из этого уравнения и первого уравнения
исходной системы составим новую систему
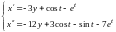 ,
(6.5)
,
(6.5)
из
первого уравнения которой выражаем
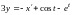 и, подставляя во второе, получаем
и, подставляя во второе, получаем
 .
Соответствующее характеристическое
уравнение
.
Соответствующее характеристическое
уравнение
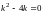 имеет корни
имеет корни
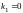 ,
,
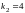
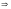
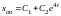 .
Частное решение ищем в виде
.
Частное решение ищем в виде
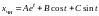 .
После определения коэффициентов получаем
.
После определения коэффициентов получаем
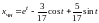 .
Следовательно
.
Следовательно
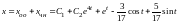 .
Найдя производную
.
Найдя производную
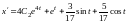 ,
получаем
,
получаем
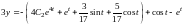 .
Таким образом, общее решение исходной
системы имеет вид
.
Таким образом, общее решение исходной
системы имеет вид
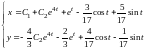 .
.
Подставляя начальные условия, определяем значения постоянных и :
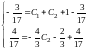
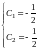 .
.
Итак, частное решение исходной системы, удовлетворяющее начальным условиям, имеет вид
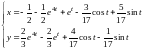 .
.
Задачи и упражнения для самостоятельного решения
Решить задачи: №№ 4324.1–4324.4 [2], а также задачи:
1)
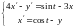 ;
2)
;
2)
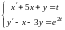 .
.
Форма отчетности: устный опрос, контрольная работа.
Занятие № 24 Понятие о теории устойчивости ляпунова
Литература: [1], c. 113-127.
Основные понятия
Решение
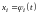 системы дифференциальных уравнений
системы дифференциальных уравнений
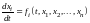
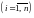 ,
(7.1)
,
(7.1)
определенное
при всех
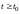 ,
называется устойчивым
(по Ляпунову), если для любого
,
называется устойчивым
(по Ляпунову), если для любого
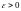 существует такое
существует такое
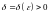 ,
что для всякого решения
,
что для всякого решения
 той же системы уравнений, начальное
значение которого удовлетворяет
неравенству
той же системы уравнений, начальное
значение которого удовлетворяет
неравенству
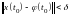 ,
при всех
выполняется неравенство
,
при всех
выполняется неравенство
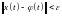 .
.
Решение
системы дифференциальных уравнений
(7.1) называется асимптотически
устойчивым,
если оно устойчиво и существует такое
 ,
что для всякого решения
той же системы уравнений, начальное
значение которого удовлетворяет
неравенству
,
что для всякого решения
той же системы уравнений, начальное
значение которого удовлетворяет
неравенству
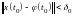 ,
справедливо предельное равенство
,
справедливо предельное равенство
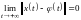 .
.
Если решение не является устойчивым, то будем называть его неустойчивым.
Рассмотрим случай, когда система (7.1) имеет вид
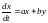 ,
,
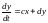 .
(7.2)
.
(7.2)
Эту
систему часто называют динамической
системой, а
координатную плоскость
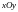 – ее фазовой
плоскостью.
Если
– ее фазовой
плоскостью.
Если
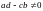 ,
то система (7.2) имеет единственное решение
(положение
равновесия):
,
то система (7.2) имеет единственное решение
(положение
равновесия):
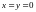 .
Качественное поведение фазовых
кривых
(траекторий)
вблизи положения равновесия определяется
собственными числами матрицы коэффициентов
этой системы, т.е. корнями характеристического
уравнения
.
Качественное поведение фазовых
кривых
(траекторий)
вблизи положения равновесия определяется
собственными числами матрицы коэффициентов
этой системы, т.е. корнями характеристического
уравнения
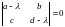 .
Рассмотрим все возможные случаи корней
.
Рассмотрим все возможные случаи корней
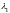 и
и
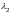 характеристического уравнения.
характеристического уравнения.
1)
Если
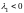 ,
,
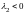 – действительные числа и
– действительные числа и
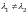 ,
то положение равновесия
,
то положение равновесия
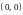 – устойчивый
узел.
– устойчивый
узел.
2)
Если
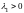 ,
,
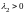 – действительные числа и
,
то положение равновесия
– неустойчивый
узел.
– действительные числа и
,
то положение равновесия
– неустойчивый
узел.
3)
Если
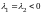 или
или
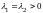 – действительные числа, то соответствующий
узел называется вырожденным.
– действительные числа, то соответствующий
узел называется вырожденным.
4) Если и – действительные числа разного знака, то положение равновесия – седло и решение системы (7.2) неустойчиво.
5)
Если
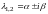 – комплексно сопряженные и
– комплексно сопряженные и
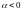 ,
то положение равновесия
– устойчивый
фокус.
,
то положение равновесия
– устойчивый
фокус.
6)
Если
– комплексно сопряженные и
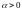 ,
то положение равновесия
– неустойчивый
фокус.
,
то положение равновесия
– неустойчивый
фокус.
7)
Если
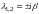 ,
то положение равновесия
– центр,
решение устойчиво.
,
то положение равновесия
– центр,
решение устойчиво.
8)
Если
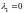 ,
– действительные числа, то решение
устойчиво, фазовыми кривыми являются
параллельные лучи, стремящиеся к одной
прямой.
,
– действительные числа, то решение
устойчиво, фазовыми кривыми являются
параллельные лучи, стремящиеся к одной
прямой.
9) Если , – действительные числа, то решение неустойчиво, фазовыми кривыми являются параллельные лучи, расходящиеся от одной прямой.
10)
Если
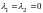 ,
то решение неустойчиво, а фазовыми
траекториями являются параллельные
прямые.
,
то решение неустойчиво, а фазовыми
траекториями являются параллельные
прямые.
Рассмотрим случай, когда система (7.1) имеет вид
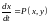 ,
,
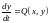 ,
(7.3)
,
(7.3)
где
и
– непрерывно дифференцируемые в
некоторой области функции. Положения
равновесия этой системы определяются
из условий
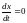 и
и
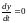 ,
т.е. из решения системы уравнений
,
т.е. из решения системы уравнений
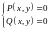 .
Для исследования положения равновесия
.
Для исследования положения равновесия
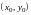 надо перенести начало координат в точку
и разложить функции
и
в окрестности этой точки в ряд Тейлора,
ограничиваясь членами первого порядка.
Тогда система (7.3) примет вид
надо перенести начало координат в точку
и разложить функции
и
в окрестности этой точки в ряд Тейлора,
ограничиваясь членами первого порядка.
Тогда система (7.3) примет вид
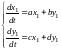 ,
где
,
где
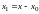 ,
,
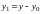 ,
,
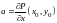 ,
,
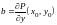 ,
,
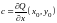 ,
,
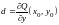 .
Тип положения равновесия
определяется далее так же, как для случая
системы (7.2). Исследовав поведение фазовых
кривых в окрестности каждого положения
равновесия, можно решить глобальную
задачу качественной теории систем
дифференциальных уравнений
– установить поведение фазовых кривых
на всей фазовой плоскости.
.
Тип положения равновесия
определяется далее так же, как для случая
системы (7.2). Исследовав поведение фазовых
кривых в окрестности каждого положения
равновесия, можно решить глобальную
задачу качественной теории систем
дифференциальных уравнений
– установить поведение фазовых кривых
на всей фазовой плоскости.
